TỔNG HỢP ĐIỀU KHIỂN THÍCH NGHI HỆ THỐNG
CHỐNG BÓ CỨNG BÁNH XE Ô TÔ KHI PHANH TRÊN
CƠ SỞ MÔ HÌNH MẠNG NƠ RON XUYÊN TÂM - RBFN
PGS. TS. LÊ HÙNG LÂN
ThS. NGUYỄN VĂN TIỀM
Bộ môn Điều khiển học
Khoa Điện – Điện tử
Trường Đại học Giao thông Vận tải
Tóm tắt: Hệ thống chống bó phanh (ABS – Anti-lock braking system) có vai trò rất quan
trọng trong việc đảm bảo chất lượng khi phanh và tính dẫn hướng của ôtô. Đa số các bộ điều
khiển ABS có bán ở trên thị trường đều dựa trên nguyên lý điều khiển on-off. Trên các xe ôtô
hiện đại đều được trang bị ở mỗi bánh xe một bộ điều khiển ABS, mục đích là để điều khiển độ
trượt tương đối giữa bánh xe và mặt đường khi phanh. Bài báo này đưa ra phương pháp tổng
hợp hệ thống điều khiển thích nghi độ trượt này trên cơ sở mạng nơ ron. Đánh giá hiệu quả
của phương pháp thông qua các kết quả mô phỏng máy tính.
Summary: The anti-lock braking system (ABS) is an important component of a complex
steering system for modern automobiles. Most of the controllers available in the market are
based on on-off controlling principle. All automobiles of the latest type are fitted with an ABS
controller, aiming to maintain a specified tire slip for each wheel during braking. This paper
proposes a model of an adaptive controller, based on network control to regulate the tire-slip.
Simulation and test results are presented to form assessment of the method.
ĐT
I. ĐẶT VẤN ĐỀ
HTĐK (hệ thống điều khiển) ABS phải đảm bảo độ trượt tương đối giữa bánh xe và mặt
đường ở giá trị độ trượt tối ưu λ0 = 0,2 (20%) khi phanh, khi đó sẽ đạt được quá trình phanh tối
ưu và xe không bị mất lái, ổn định tính dẫn hướng. Khi điều kiện mặt đường thay đổi thì tính
phi tuyến của ma sát giữa lốp xe và mặt đường cũng thay đổi theo [1].
Có ABS
Không có ABS
Hình 1. Hình ảnh khi phanh có ABS và không có ABS
Phanh không có ABS trên đường tuyết.
Hình ảnh khi phanh có ABS và không có ABS như hình 1. Trong bài báo [1] chúng tôi đã
sử dụng lôgic mờ để tự động nhận dạng hệ số ma sát mặt đường, sau đó thiết kế bổ sung mạch
điều khiển thích nghi, kết quả mô phỏng cho thấy quá trình phanh luôn đảm bảo được độ trượt ở
giá trị tối ưu, hướng sử dụng logic mờ cho bài toán này cũng được [2] đề cập tới. Trong bài báo
này chúng tôi sẽ đưa ra một phương pháp sử dụng mạng nơ ron xuyên tâm để nhận dạng hệ số
ma sát mặt đường và thiết kế các mạch điều khiển bổ sung với mục đích khống chế độ trượt
luôn ở giá trị tối ưu khi phanh.
II. MÔ HÌNH ĐỘNG HỌC BÁNH XE Ô TÔ
Các biểu thức của chuyển động của một trong 4 bánh xe ô tô [3] như sau:
x
Fvm
b
T
x
rFJ
−=
−=ω
&
&
(1)
trong đó: m là ¼ khối lượng xe; v là tốc độ của xe; ω là tốc độ của bánh xe; Fz là lực pháp
tuyến; Fx là lực ma sát bánh xe. Tb là mô men phanh; r là bán kính bánh xe; J là mô men quán
tính.
Độ trượt của bánh xe được định nghĩa như sau [3]: v
rv ω−
=λ , (2)
khi bánh xe bị bó cứng hoàn toàn thì λ = 1, khi xe chuyển động tự do thì λ = 0.
ĐT Lực ma sát bánh xe Fx được định nghĩa bởi: Fx = Fzμ(λ, μH, α, Fz, v), (3)
ở đây μ(λ, μH, α, Fz, v) là hệ số ma sát giữa lốp xe và mặt đường, đây là một hàm phi tuyến
với một kiểu phụ thuộc vào độ trượt [1], [3], μH là hệ số ma sát lớn nhất và thay đổi theo điều
kiện mặt đường, α là góc lái và ta chỉ quan tâm đến trường hợp không có góc lái (α = 0).
Với quan niệm giá trị vận tốc của xe biến đổi chậm hơn rất nhiều so với sự thay đổi của các
giá trị khác ở (3), động học của độ trượt bánh xe như sau: μ−=λ J
z
F
2
r
b
T
J
r
v
&, (4)
Do tác động trễ điều khiển một thời gian T, mô hình ABS có thể tổng hợp theo biểu thức
sau: λ, (5)
() ()() (
Ttutvt −α+λβμ−=
)
&
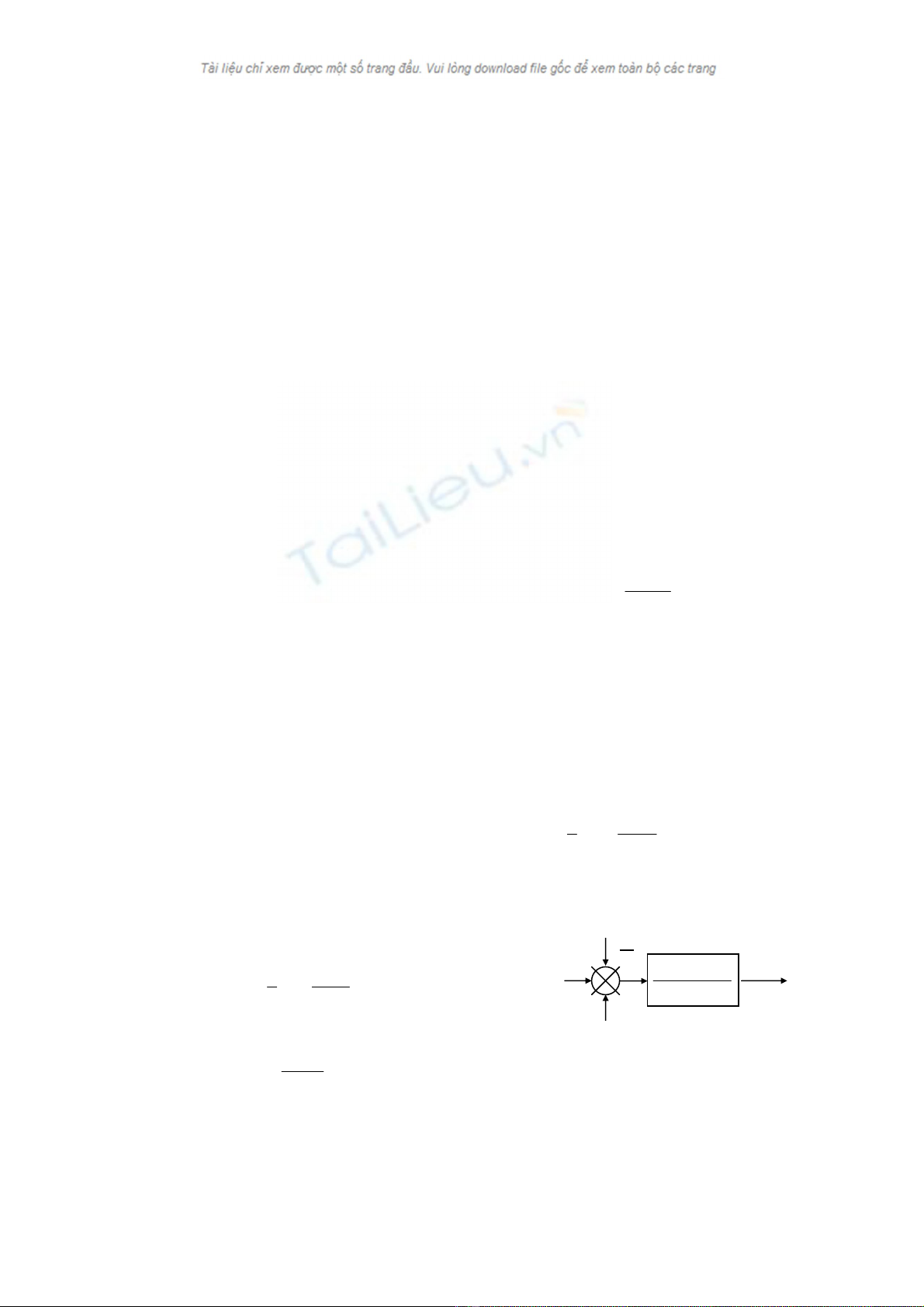
Hình 2. Mô hình đối tượng ABS.
λ
u
(
)
λf
(
)
td
b
ass
c
2++
ở đây v là một hằng số nhưng không chắc chắn,
trong đó: J
z
F
2
r
;
J
r=β=α . (6)
Theo [1], thành phần phi tuyến chưa biết sẽ có
dạng:
() ()
λβμ
α
+
=λ 1Ts
f, (7)

Sơ đồ khối của mô hình ABS như hình 2. Cũng theo [1], khi thiết kế cho trường hợp mặt
đường nhựa khô thì hàm truyền phần tuyến tính của ABS có dạng:
()
b
ass
c
sW 2
ABS_TT ++
=, trong đó: v.T
k.
b;
v.T
k..T
a;
v.T
c11 β
=
β
=
α
= (8)
Các tham số của xe [1], [3]:
[
]
2
m.kg0,1J =;
[
]
kg450m
=
;
[
]
m32,0r
=
; ;
; ;
[]
N4414Fz=
[]
kg/N584,451=β
[]
)m.kg/(132,0a =
[
]
ms14T
=
=
τ
;
[
][
s/m35h/Km126v
]
=
=
;
lấy tuyến tính đoạn k1 = 4,5 ta có: c = 0,6531; a = 129,4894; b = 4147,2.
Có nhiều phương pháp để tính tham số PID cho đối tượng (8), theo [1] tham số bộ PID là:
k
P = 2,5808.103; kI = 1,8434.105, kD = 10. (9)
Đối tượng điều khiển ABS [1] có dạng:
(
)()
[
]
tdfccuba +λ++λ−λ−=λ &&& , (10)
trong đó: là hàm phi tuyến trơn không rõ và nhiễu d(t) không rõ có giới hạn trên cho
trước, λ và u lần lượt là tín hiệu ra vào của hệ thống. Khi chưa xét đến thành phần phi tuyến thì
đối tượng có dạng (8), thường được điều khiển bằng bộ PID kinh điển:
()
λf
() ()
(
)
(
)
(
)
tekdttektektutu DIP0PID &
++==
∫
;kP, kI, kD đã biết. (11)
III. TỔNG HỢP HTĐK ABS THÍCH NGHI TRÊN CƠ SỞ MẠNG NƠ RON
ĐT
3.1. Các quan điểm tổng hợp hệ thống
Thứ nhất: giả thiết hệ thống đang sử dụng bộ PID kinh điển trong vòng điều khiển;
Thứ hai: sử dụng mạng nơ ron xuyên tâm – RBFN để nhận dạng hệ số ma sát mặt đường
và thiết kế các mạch điều khiển bổ sung cho bộ điều khiển PID.
Định nghĩa sai số bám
()
(
)
(
)
ttte d
λ
−
λ= , ta có thể viết lại (10) như sau:
(
)
[
]
1
ddfccubeeae
+
+
λ
−−−−= &&& ; ddd1 c
b
c
a
c
1
dλ−λ−λ−= &&& (12)
Bài toán đặt ra là thiết kế bổ sung mạch điều khiển thích nghi để nâng cao chất lượng điều
khiển, đặc biệt khi điều kiện mặt đường thay đổi và nhiễu có tác động mạnh vào hệ thống.
Vì là hàm phi tuyến trơn nên có thể áp dụng mạng xuyên tâm RBFN (Radial Basic
Function network) để xấp xỉ với giả thiết có đủ số hàm cơ sở
()
λf
(
)
⋅φ trên tập compact:
{}
() ()
ε+λφω=λλ=Λ≤Λ−ΛΛ=Ω ∑
=
∗
i
m
1i
iddd f;;M , (13)
trong đó: là các trọng số “lý tưởng”, ε là sai số xấp xỉ thoả mãn
∗
ωiM
ε≤ε , ci là véctơ 1

chiều thể hiện trọng tâm hàm cơ sở thứ i, i
σ
là phương sai thể hiện chiều rộng của hàm cơ sở.
Nói chung các trọng số không biết và cần đánh giá trong thiết kế bộ điều khiển. Cần
lưu ý là tập và hằng số giới hạn có thể lớn tuỳ ý.
∗
ωi
ΩM
ε
3.2. Tổng hợp HTĐK thích nghi trên cơ sở mạng nơ ron xuyên tâm - RBFN
Bằng cách đặt các biến trạng thái hệ thống , từ (12) ta có mô hình
trạng thái tương đương:
()
T
t
0
eedez ⎥
⎦
⎤
⎢
⎣
⎡ττ= ∫&
(
)
[
]
1
ddfBBuAzz
+
+
λ
+
+
=
& (14)
(15)
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
−−
=
c
0
0
B;
ab0
100
010
A
Khi điều kiện mặt đường không đổi và nhiễu tác động còn yếu có thể sử dụng bộ điều
khiển PID ban đầu (11): , với
zKu T
00 =
[
]
DPI
T
0kkkK =. (16)
Để thiết kế bổ sung mạch thích nghi ta chọn siêu mặt trượt sau:
(
)
zKts T
0
=, (17)
khi đó:
(
)
(
)
(
)
1
T
0
T
0ddfBBuAzKzKs ++λ++== &
& (18)
Nếu ta chọn luật điều khiển như sau: ,uukuu adfd0
+
+
=
(19)
ĐT
trong đó ufd là tín hiệu điều khiển phản hồi, uad là tín hiệu điều khiển thích nghi và k > 0 thì:
(
)
(
)
(
)
(
)
dfBKBuKBskKBuKAzKBdKs T
0ad
T
0
T
0fd
T
0
T
01
T
0+λ+++++=
&. (20)
Đặt:
()
(
)
(
)
,ssigndssign
ˆ
f
ˆ
uMad +θ+λ−= (21)
với 0,dd MM >ηη+= bất kỳ,
(
)
λf
ˆ là đánh giá ước lượng của
(
)
λf và để ý đến quan hệ
, ta có thể biến đổi thành phần thứ ba của biểu thức (20) như sau:
() ()
ε+λ
∗
=λ ff
()()
(
)
(
)
(
)
(
)
()
(
)
BdKfBKssigndssign
ˆ
f
ˆ
BKdfuBK T
0
T
0M
T
0ad
T
0+ε+λ++θ+λ−=+λ+ ∗
(
)
(
)
(
)
(
)
(
)
()
()
ssignddBKssign
ˆ
BKff
ˆ
BK M
T
0
T
0
T
0++θ+ε+λ−λ−= ∗,
khi đó, nếu tiếp tục đặt:
[
]
AzKBKdu T
0
1
T
01fd
−
−−= , (22)
thì cuối cùng ta sẽ có:
(
)
(
)
0
T
0
T
0
1
T
01
T
0
T
01
T
0BukKAzKBKdBKAzKBdKs +−−++= −
&
(
)
(
)
(
)
(
)
(
)
()
()
ssignddBKssign
ˆ
BKff
ˆ
BK M
T
0
T
0
T
0++θ+ε+λ−λ− ∗,
()
(
)
()
()
ssignddBKssign
ˆ
BK
~
BKBskKs M
T
0
T
0
m
1i
ii
T
0
T
0++θ+ε+φω−= ∑
=
&;∗
ω−ω=ω iii ˆ
~
.
(23)
Chọn hàm Lyapunov như sau:
()
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛θ−ε
η
−ω
η
−= ∑
=
m
1i
2
M
T
0
2
2
i
T
0
1
2ˆ
BK
1
~
BK
1
s
2
1
tV (24)
và các luật thích nghi: , (25)
0;s
ˆ1i1 >ηφη−=ω
&
0;s
ˆ22 >ηη=θ
&. (26)
(
)
λf
ˆ
ĐT
Với cách chọn hàm V(t) như (24) thì hàm V(t) là xác định dương, vì .
0ckBK D
T
0<−=
Khi đó:
()
(
)
⎟
⎠
⎞
⎜
⎝
⎛θ−θ−ε
η
−ωω
η
−= ∑&
&
&
&ˆˆ
BK
1
ˆ
~
BK
1
sstV M
T
0
2
ii
T
0
1
(
)
s
ˆ
BK
~
BsKss M
T
0
m
1i
ii
T
0θ−ε+φω+= ∑
=
&
()
(
)
(
)
()
.s
ˆ
BKssign
ˆ
BsKssigndssdBKssBKBskK T
0
T
0M
T
0M
T
0
2T
0θ−θ+++ε+ε+=
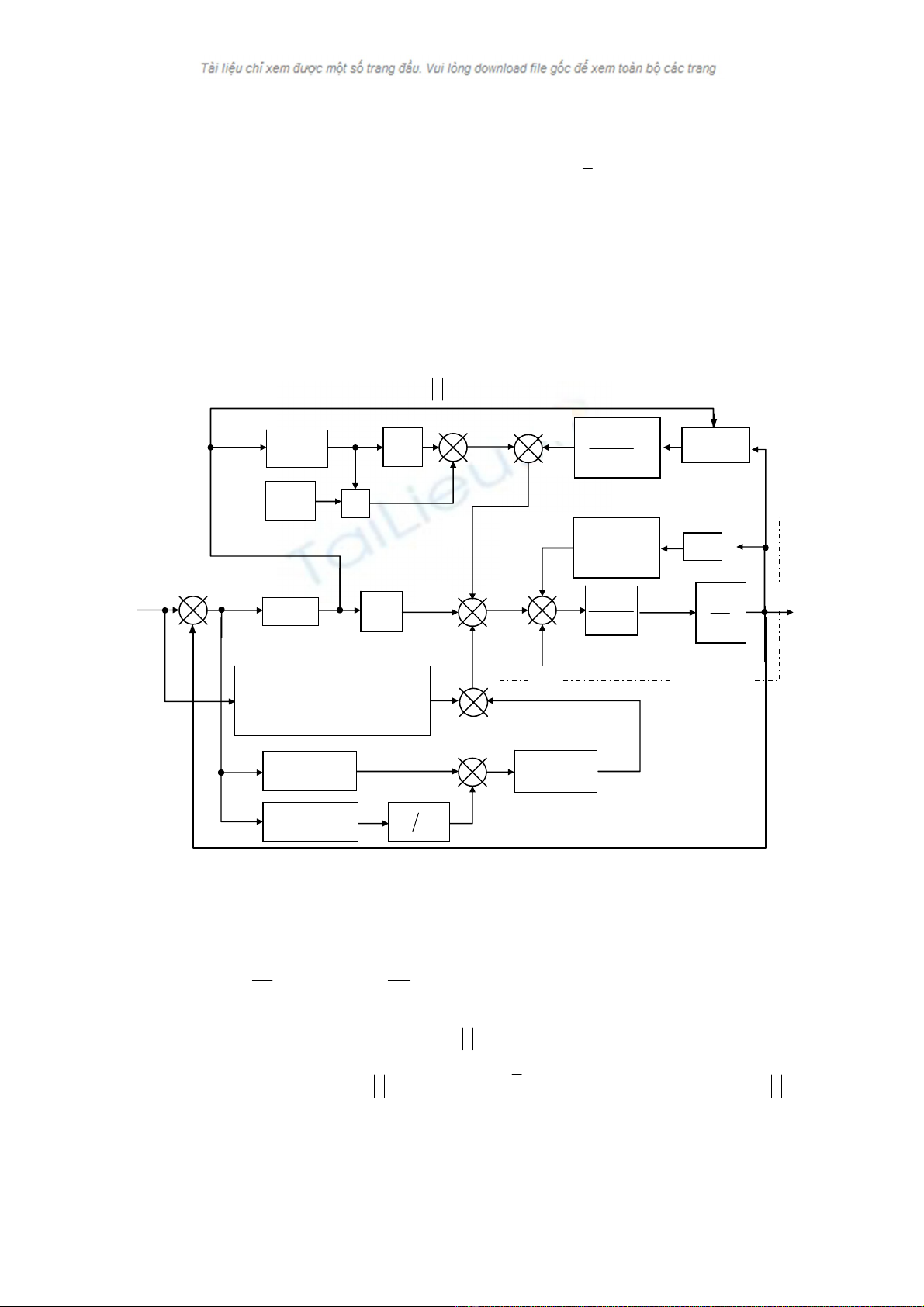
Hình 3. Sơ đồ cấu trúc điều khiển ABS thích nghi trên cơ sở mạng nơ ron RBFN.
(
)
λ
f
(
)
tu
0
ku
fd
u
ad
u
(
)
t
λ
0d λ=λ
(-)
(-)
(-)
(-)
k
×
DI bkk −
DP akk − dtd
sign θ
ˆ
()
λμ
β
α
+
1Ts
1Ts
+
α
vs
1
(
)
td
()
ddd1 ca
c
1
dλ−λ−λ−= &&&
theo côn
g
thức
(
12
)
ABS
β
α
+
1Ts ∑φω ii
ˆ
PID
M
d
(
)
1
D
ck −