08/2010
1
Chương 2. Biến dạng dẻo và cơ tính
2.1 Biến dạng dẻo và phá hủy
2.2 Các đặc trưng cơ tính
2.3 Nung kim loại đã qua biến dạng dẻo
Chương 2. Biến dạng dẻo và cơ tính
2.1 Biến dạng dẻo và phá hủy
2.1.1 Khái niệm
-Biến dạng: Sự thay đổi kích thước, hình dạng
của vật liệu dưới tác dụng của tải trọng
-Biến dạng đàn hồi: Biến dạng mất đi khi bỏtải
P < σđh
-Biến dạng dẻo: Biến dạng còn tồn tại khi bỏtải
P > σđh
08/2010
2
2.1 Biến dạng dẻo và phá hủy
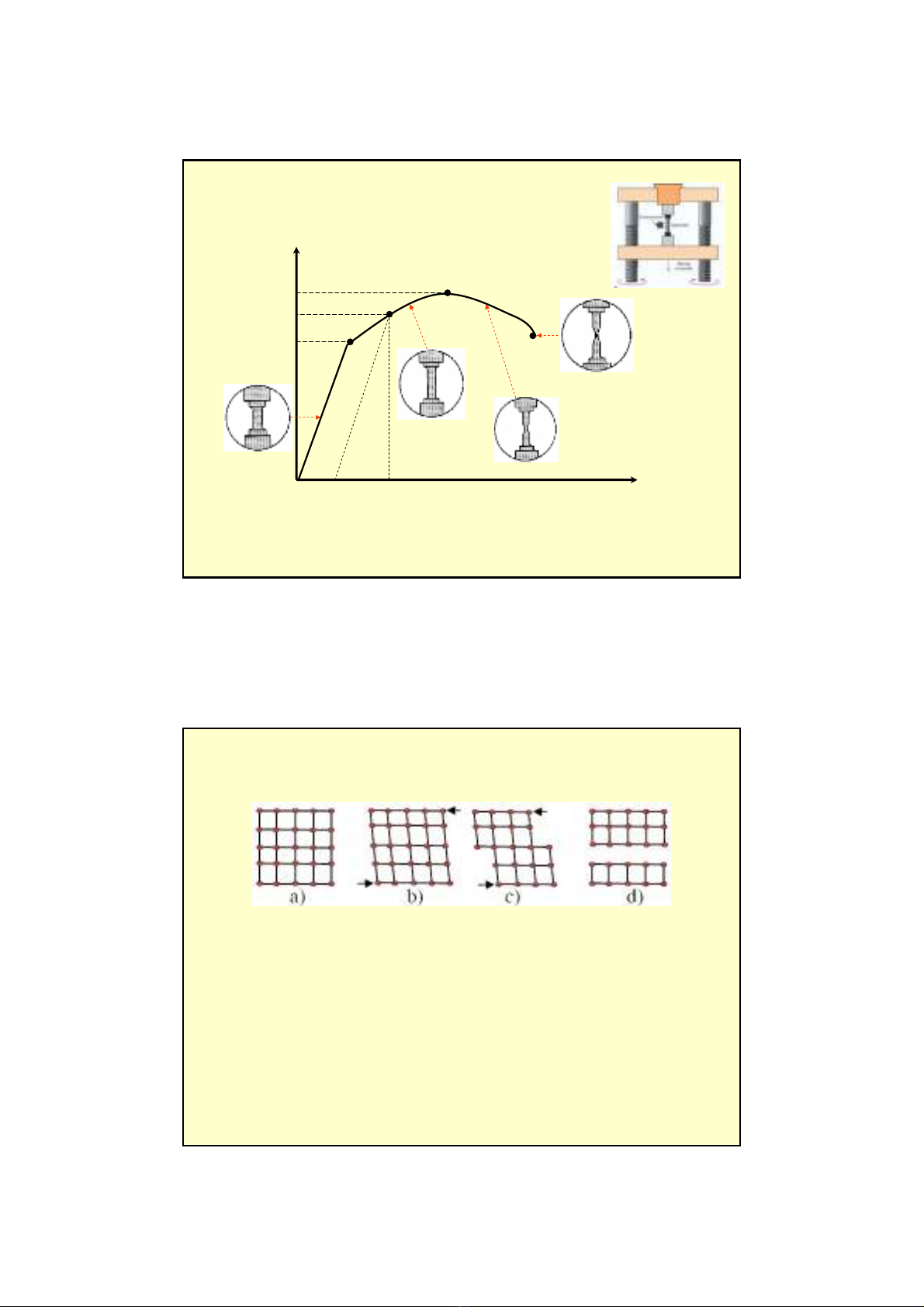
Độ dãn dài
Δ
l
Tảitrọng F
Fđh
a1
e
Faa
b
c
Fb
a2
0
Biểu đồ tải trọng – biến dạng
2.1 Biến dạng dẻo và phá hủy
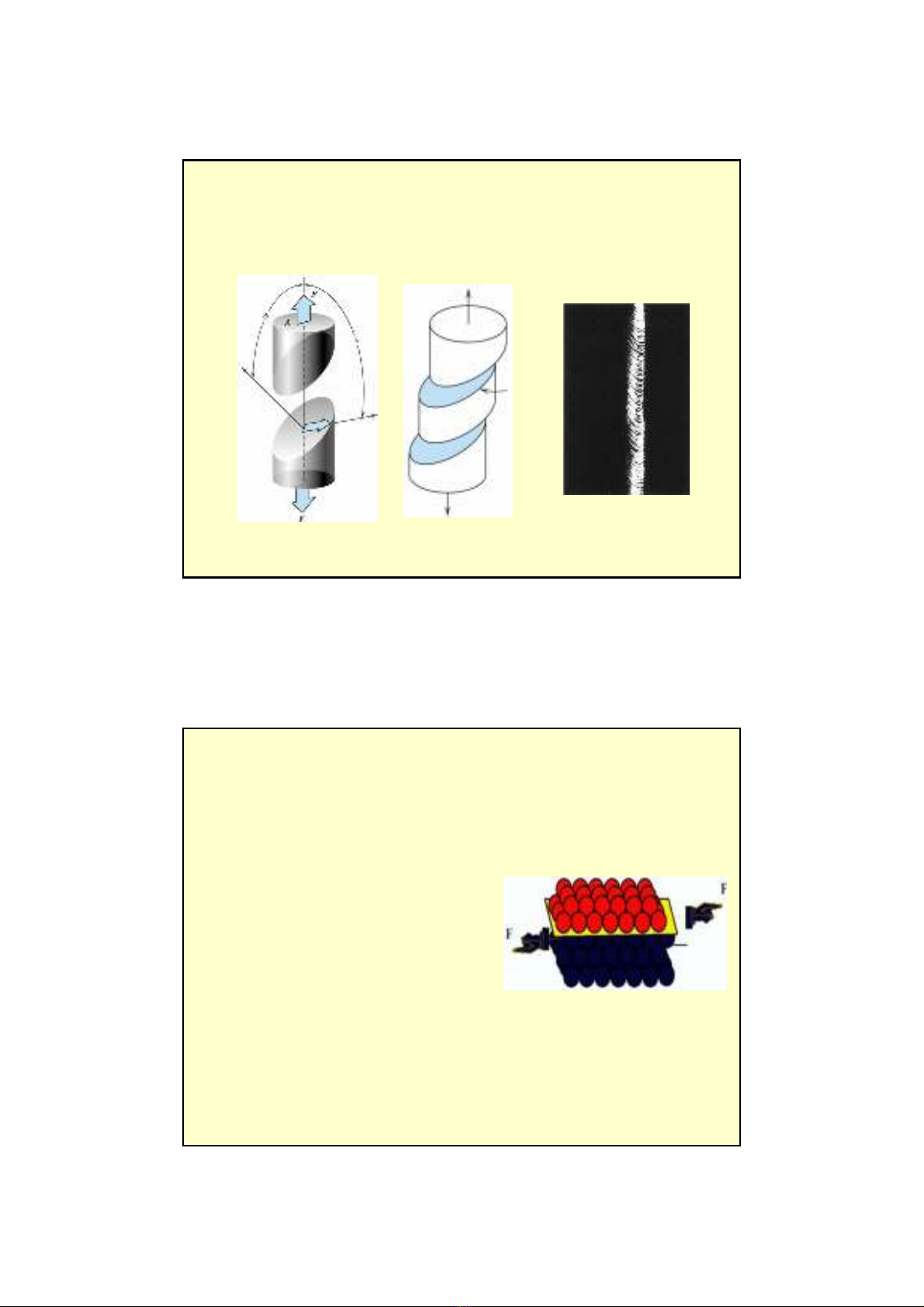
a) Ban đầu: các nguyên tửchỉdao động xung quanh vịtrí cân
bằng
b) Biến dạng dàn hối: các nguyên tửxê dịch trong phạm vi hẹp
nhỏ hơn hằng sốmạng, có thểtrởvềvịtrí ban đầu khi bỏtải
c) Biến dạng dẻo: các nguyên tửxê dịch trong phạm vi lơn hơn
hằng sốmạng (trượt), không thểtrởvềvịtrí ban đầu khi bỏtải
d) Phảhủy: liên kết giữa các nguyên tửbịcắt rời
08/2010
3
2.1.2 Trượt đơn tinh thể
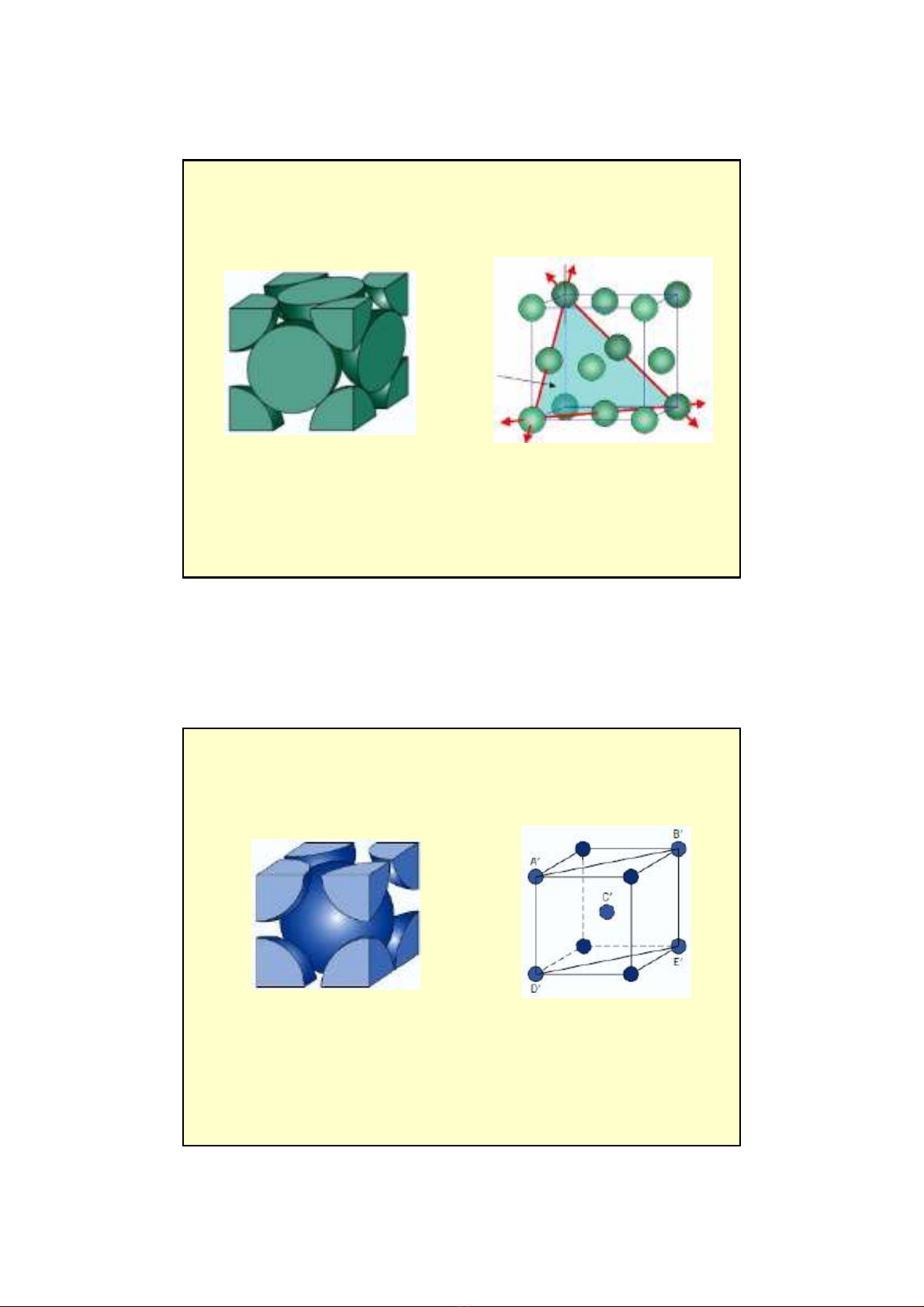
Khái niệm: Trượt là sựchuyển dời tương đối giữa các phần của tinh thểtheo
những mặt và phương nhất định được gọi là phương trượt và mặt trượt.
Phương trượt
Mặttrượt
Trượt trong đơn
tinh thểZn
Hiệntượng trượt trong đơn
tinh thể
2.1.2 Trượt đơn tinh thể
a) Các mặt và phương trượt
Mặt trượt: Mặt (tưởng tượng) phân cách giữa hai mặt
nguyên tửdày đặc nhất tại đóxảy ra hiện tượng trượt
Mặt dày đặc nhất?
Điều kiện:
- Liên kết giữa các nguyên tửbềvững nhất
-Khoảng cách giữa hai mặt là lớn nhất
Phương trượt: Phương có mật độ nguyên tửlớn nhất
Hệ trượt: sựkết hợp giữa một phương trượt và một mặt trượt
08/2010
4
2.1.2 Trượt đơn tinh thể
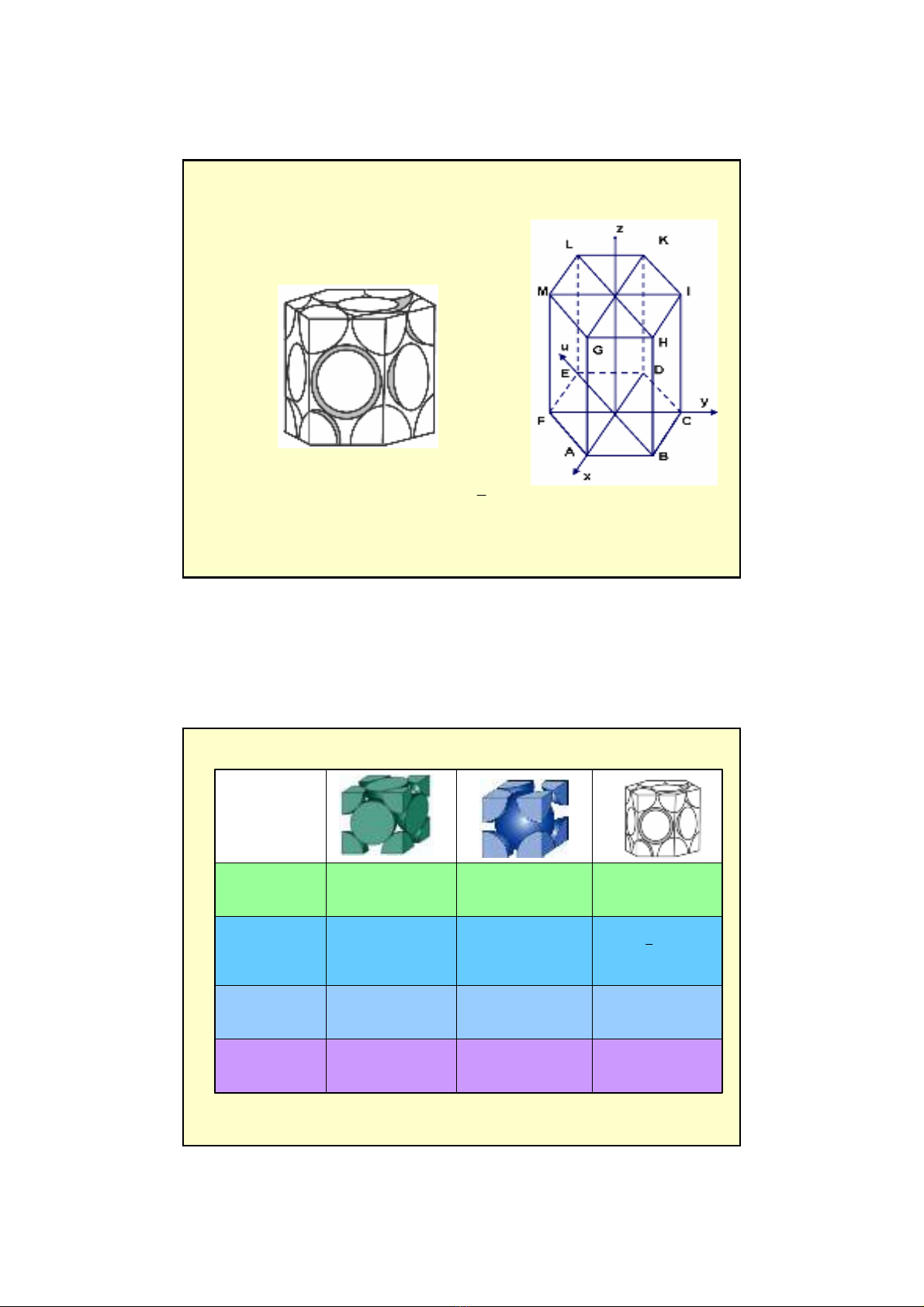
Hệ trượt trong mạng A1
Họmặt trượt: {111}, số lượng: 4
Họ phương trượt <110>, số lượng: 3
Hệ trượt = số phương trượt x sốmặt trượt = 12
2.1.2 Trượt đơn tinh thể
Hệ trượt trong mạng A2
Họmặt trượt: {110}: 6
Họ phương trượt <111>: 2
Hệ trượt = số phương trượt x sốmặt trượt = 12
08/2010
5
2.1.2 Trượt đơn tinh thể
Hệ trượt trong mạng A3
Mặt xếp chặt nhất: {0001}: 1
Họ phương xếp chặt nhất : 3
Hệ trượt = số phương trượt x sốmặt trượt = 3
>< 0211
Tiα, Zn, Mg, BeFeα, Cr, W, VFeγ, Ai, Cu, Au
Kim loại
31212
Hệ trượt
(3)<111> (2)<110> (3)
Họ phương
trượt
{0001} (1){110} (6){111} (4)
Họmặt
trượt
Kiểu mạng
>< 0211