4. Ph−¬ng tr×nh c¬ b¶n cña chuyÓn ®éng quay
cña vËt r¾n quanh mét trôc cè ®Þnh:
Δ
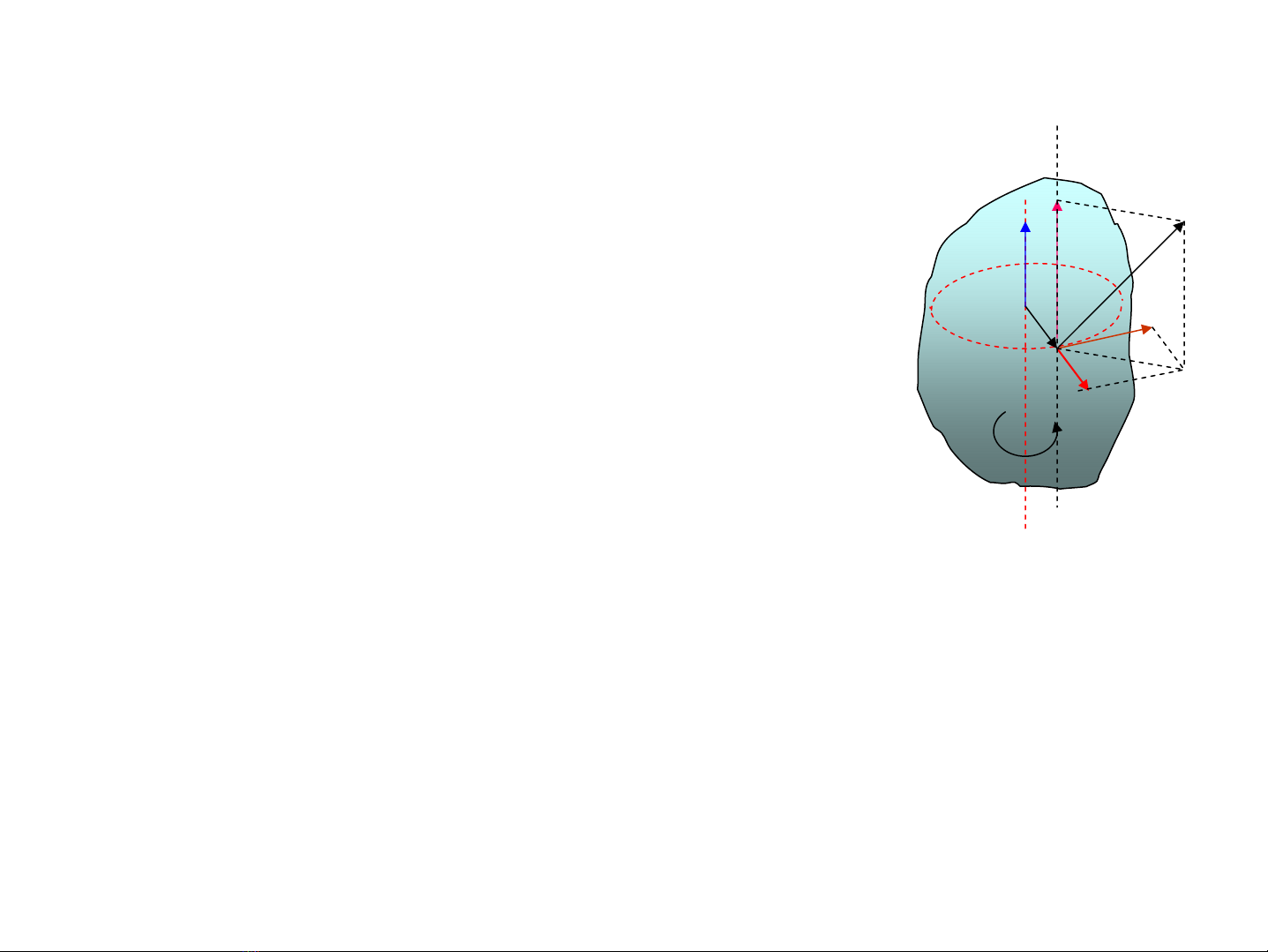
4.1.T¸c dông cña lùc
tn FF
r
r
r
r
++= z
FF
z
F
r
t
F
r
n
F
r
F
r
z
F vμ
r
r
n
F®ång ph¼ng víi trôc
quay kh«ng g©y quay v×
Δ//
z
F r
n
F
r
xuyªn t©m
M
r
r
r
Trong chuyÓn ®éng quay cña vËt r¾n quanh
mét trôc chØ cã thμnh phÇn tiÕp tuyÕn víi
quÜ ®¹o cña ®iÓm ®Æt míi cã t¸c dông thùc sù
t
F
r
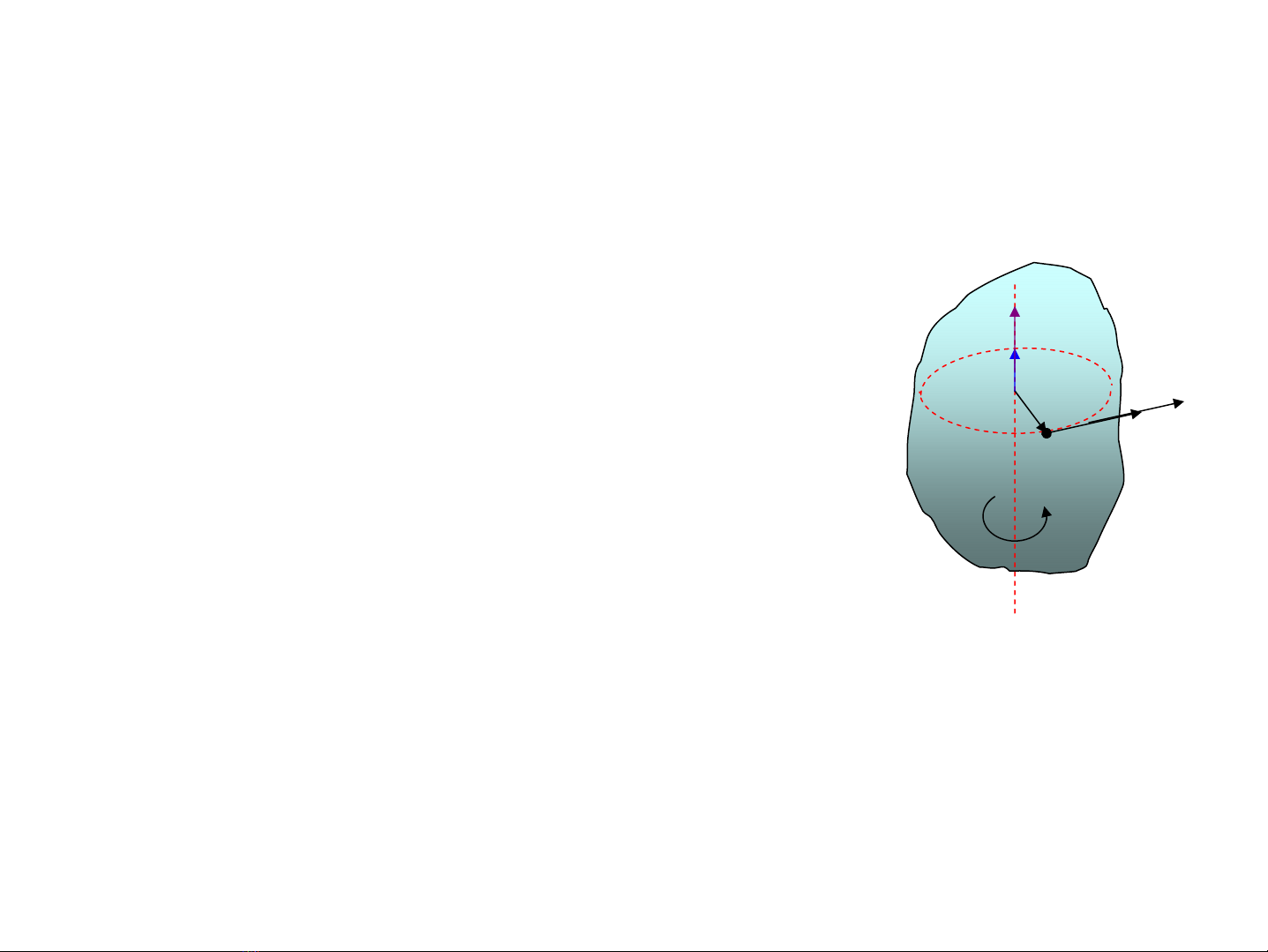
M«men cña lùc t
F
r
r
r
×= rM tt F.rsin.F
α
r.M
β
r
ti
M
r
i
r
r
ti
a
r
ti
F
r
Δ
mi
O
4.2. Ph−¬ngtr×nhc¬bncña
chuyÓn ®éng quay
ChÊt ®iÓm thø i titi Fa
r
r
= mi
tiiti Fra
r
r
r
r
×=×
ii r m
).r(r)r.r.()r(ra iiiiiiti β−β=×β×=×
r
r
r
r
r
r
r
r
r
r
r
i
r 0).r(r ii =β
r
r
r
titii MFr.
r
r
r
r
=×=β
2
ii rm
∑
∑=β ti
M.)(
r
r
2
ii rm
M
r
r
=β I
M«men cña lùc ®èi víi trôc quay
chÝnh lμm«men cña lùc ®èi víi O -
giao ®iÓm cña trôc víi mÆt ph¼ng cña
quü ®¹o ®iÓm ®Æt lùc
t
F
r
M
r
r=β I I)( =
∑
2
ii rm M«men qu¸n tÝnh cña
vËt ®èi víi trôc quay
MMti
r
r
=
∑Tæng hîp m«men cña c¸c lùc g©y quay
I
M
r
r=β Gia tèc gãc ~M vμ~ nghÞch víi I
I <-> m vμM<->F
4.3. TÝnh m«men qu¸n tÝnh cña vËt ®èi víi trôc
quay:
0
Δ
Thanh ®Òu: Khèi l−îng M, dμiL
2
L
2
- L
dx
x
dx
M
.L
x dI 2
=
12
ML
dx.
M
dx
M
.
2
2
L
2
L
2
L
2
L
=== ∫∫ −−
22
0x
LL
x I
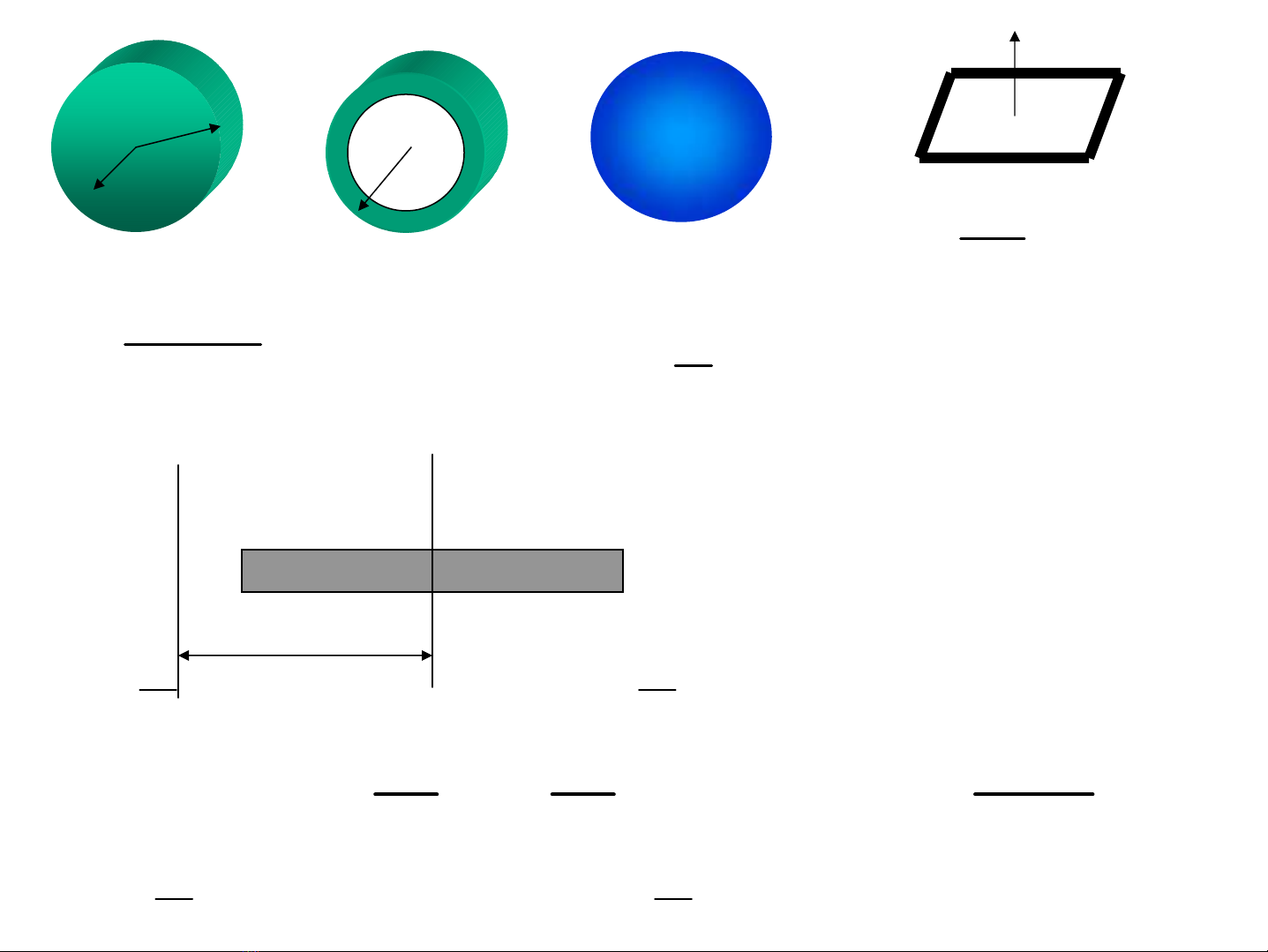
2
MR2
0=I
R
2
0MR=I2
0MR
5
2
=I
)ba(
12
M22
0+=I
a
b
0
Δ
Δ
2
0MdII +=
2
Md
12
2
ML
dx.
M
dx
M
.
2
L
2
L
2
L
2
L
+=
−
+=
−
+=
Δ∫∫ 2
x)(d
LL
2
x)(d I
d
M«men QT cña vËt r¾n
®èi víi trôc bÊt kú =...
§Þnh lý Stene-
Huyghen:
0
Δ 0
Δ
0
Δ
5. M«men ®éng l−îngcñahÖchÊt®iÓm
5.1. M«men ®éng l−îngcñahÖchÊt
®iÓm ®èi víi gèc O
HÖ chÊt ®iÓm M1, M2, ...,Mn
cã khèi l−îng m1, m2, ..., mn
n21 v,...,v,v
r
r
r
Cã vËn tèc
n21 r,...,r,r
r
r
r
VÞ trÝ ®èi víi gèc O
M«men ®éng l−îngcñahÖ®èivíiO
iiii vmrLL
r
r
r
r
∑
∑
×==
M«men ®éng l−îng cña hÖ
chÊt ®iÓm quay quanh trôc Δ
∑
∑
ω==
i
iii ILL
r
r
r