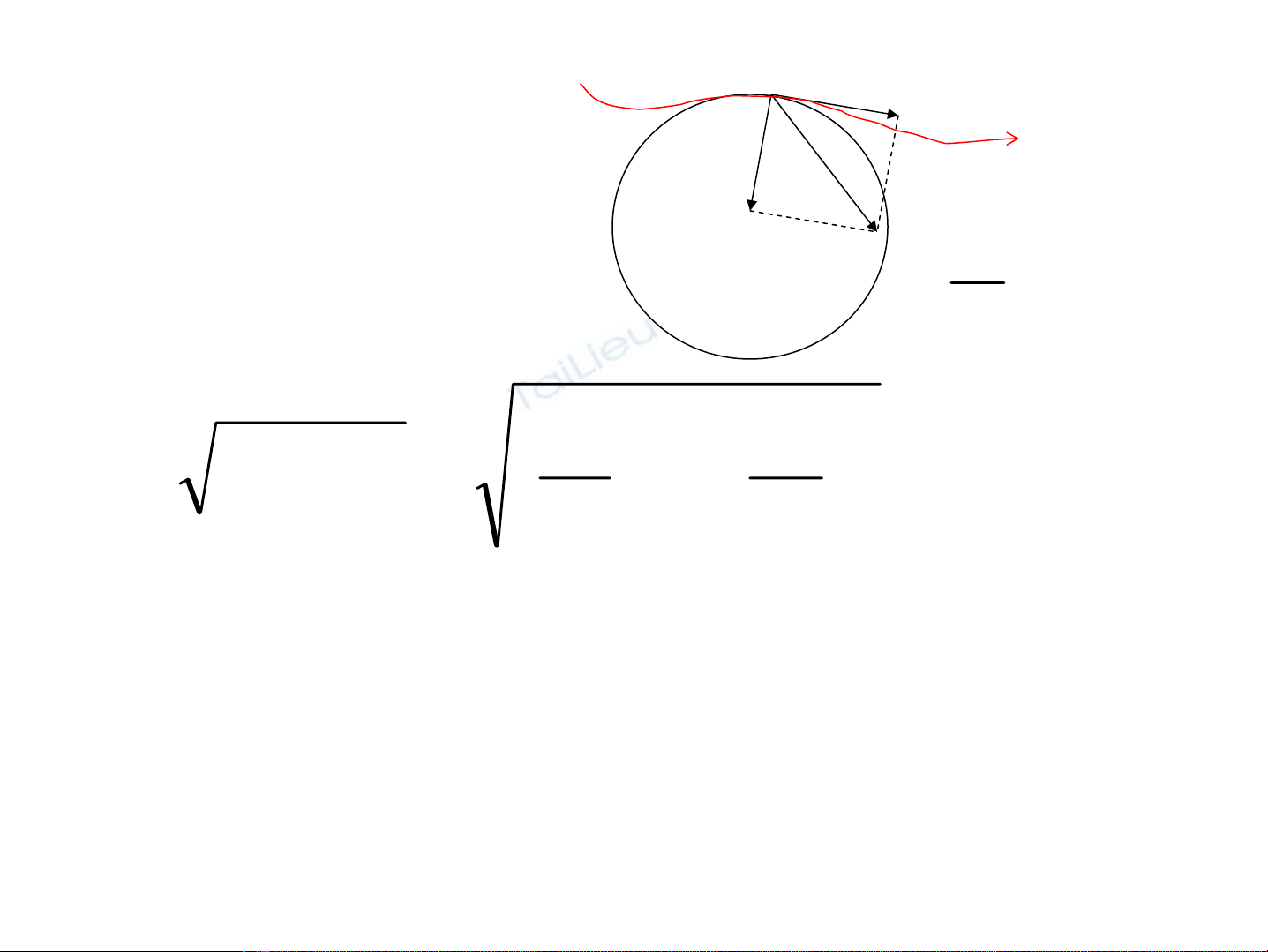
a
r
t
a
r
n
a
r
nt aaa
r
r
r
+
=
2
2
22
n
2
t)
R
v
()
dt
dv
(aaa +=+=
KÕt luËn
•a
n=0 -> chuyÓn ®éng th¼ng
•a
t=0 -> chuyÓn ®éng cong ®Òu
•a=0 -> chuyÓn ®éng th¼ng ®Òu
R
1®é cong
cña quÜ
®¹o
4. Mét sè d¹ng chuyÓn ®éng c¬ ®Æc biÖt
4.1. ChuyÓn ®éng th¼ng biÕn ®æi ®Òu:
OM
0consta == n
a
r
const
dt
dv
aa t=== ∫+== 0
vatadtv
∫+=+=⇒+== tv
2
at
dt)vat(svat
dt
ds
v0
2
00
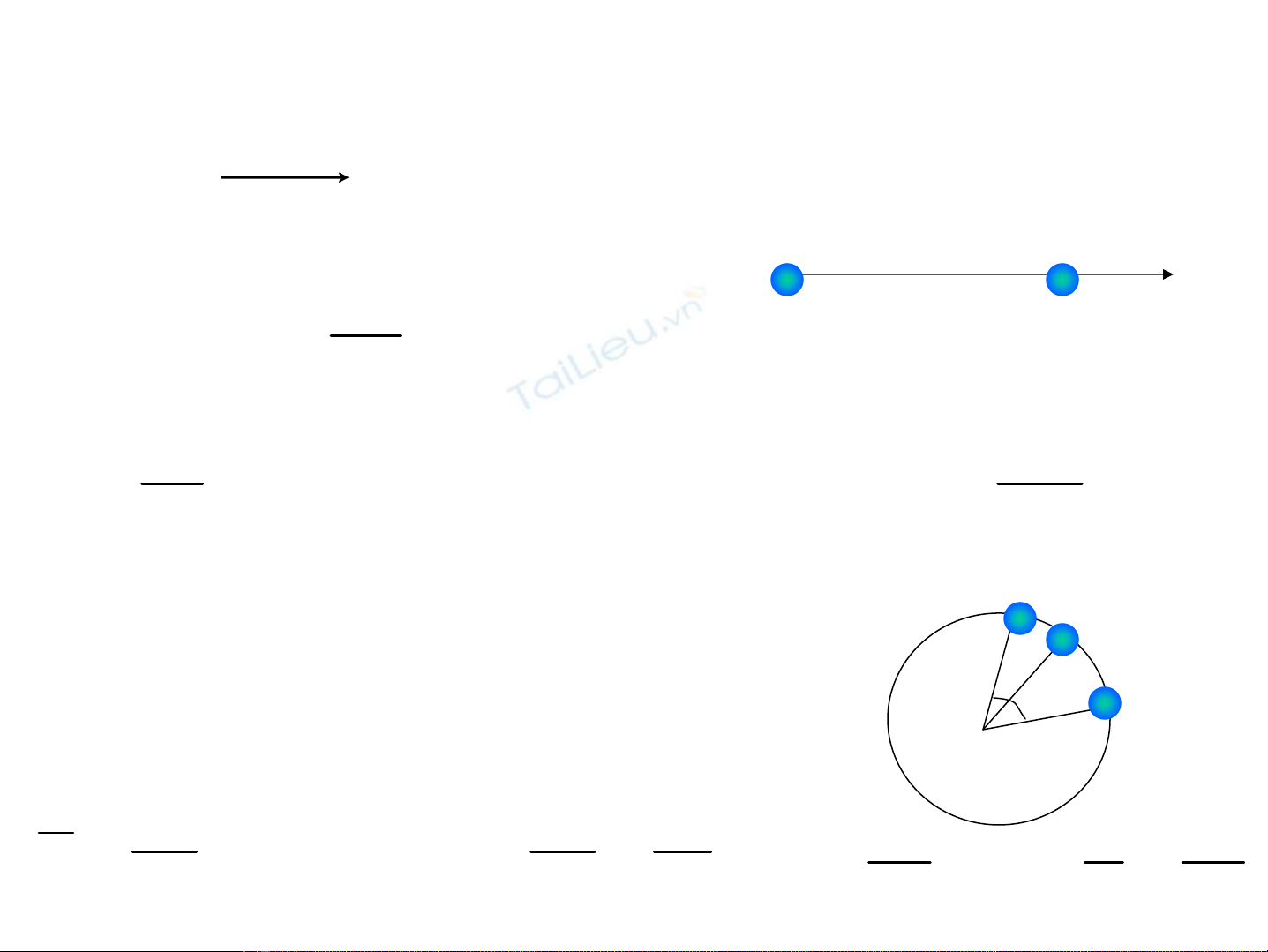
4.2. ChuyÓn ®éng trßn
T¹i M: t
T¹i M’: t’=t+Δt=> OM quÐt Δθ O
tΔ
θ
Δ
=ω dt
d
t
lim 0t
θ
=
Δ
θ
Δ
=ω →Δ π
ω
==ν
ω
=2T
12
T ;
v2-v20=2as
θ
Δ
M
M’
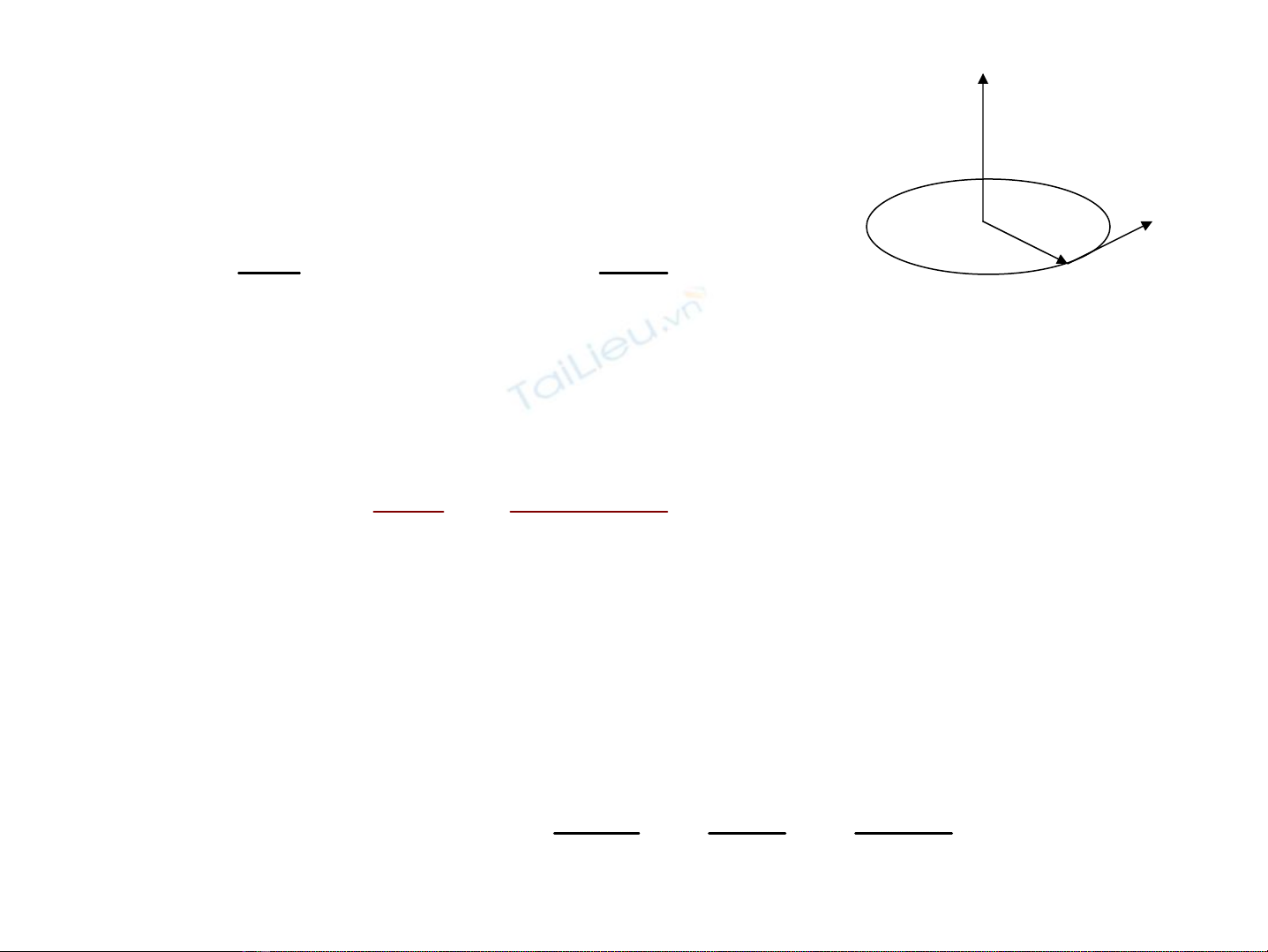
v vμ
r
r
ω
Quan hÖ gi÷a
θΔ=Δ= .RsMM
(
ω=
Δ
θ
Δ
=
Δ
Δ
→Δ→Δ .R
t
.Rlim
t
s
lim 0t0t
ω
=
R.v Rv
r
r
r
×
ω
=
⇒
HÖ qu¶: 2
22 R
R
)R(
R
vω=
ω
==
n
a
Gia tèc gãc: T¹i
ω
r
,t
ω
r
v
r
R
r
O
Qui t¾c tam diÖn thuËn
2
2
dt
d
dt
d
t
θ
=
ω
=
Δ
ωΔ
=β →Δ 0t
lim
ω
Δ
+
ω
=
ω
Δ
+
=
r
r
r
',tt't
T¹i M’:
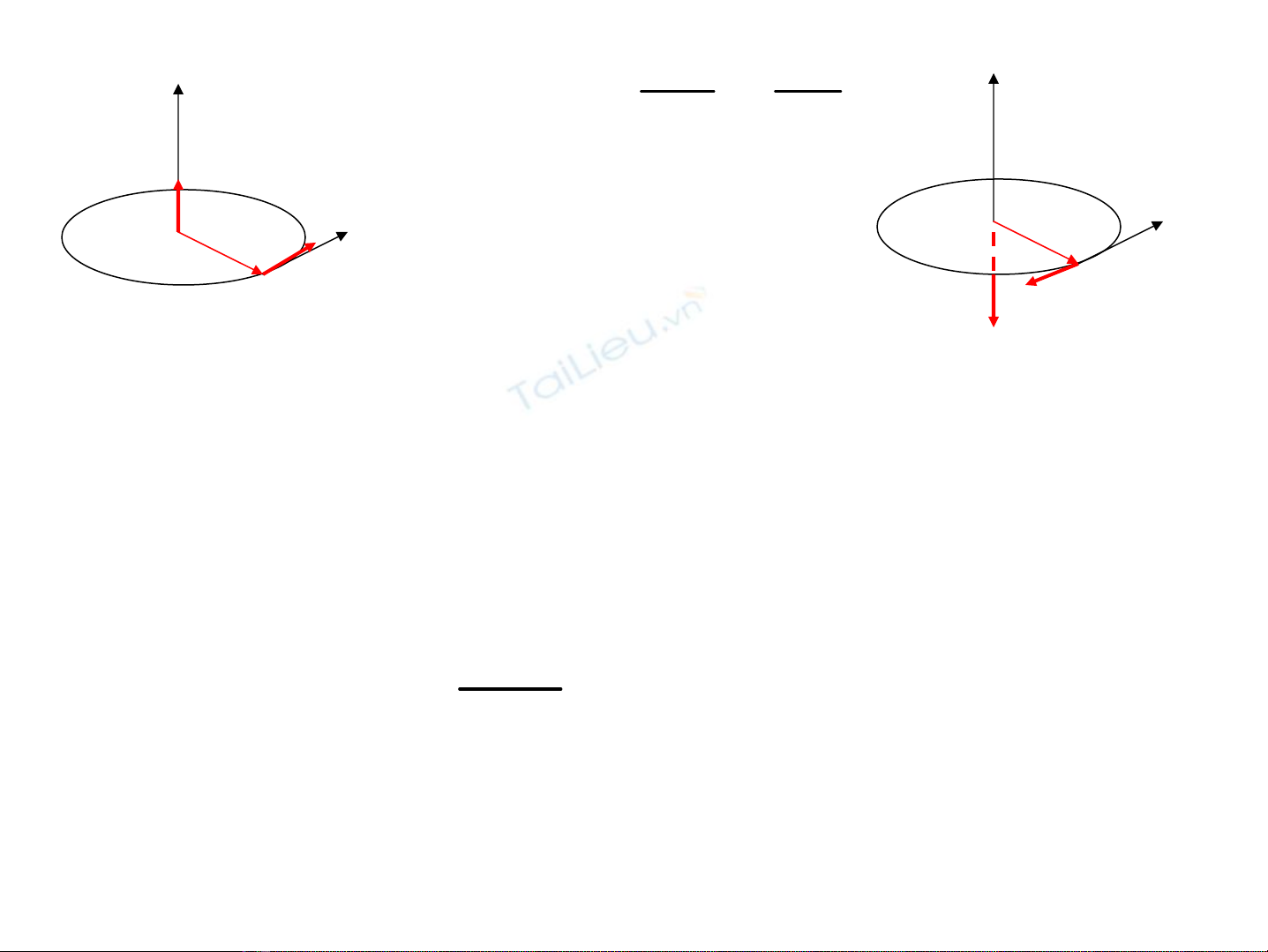
ω
r
v
r
R
r
O
M
t
a
r
β
r
ω
r
v
r
R
r
O
M
t
a
r
β
r
Qui t¾c tam diÖn thuËn
dt
d
t
lim 0t
ω
=
Δ
ω
Δ
=β →Δ
r
r
r
R
r
r
r
×β=
t
a
βθ=ω−ω
ω+
β
=θ
ω
+
β
=
ω
2
t
2
t
t
2
0
2
0
20
T−¬ngtùnh−trong chuyÓn ®éng th¼ng:
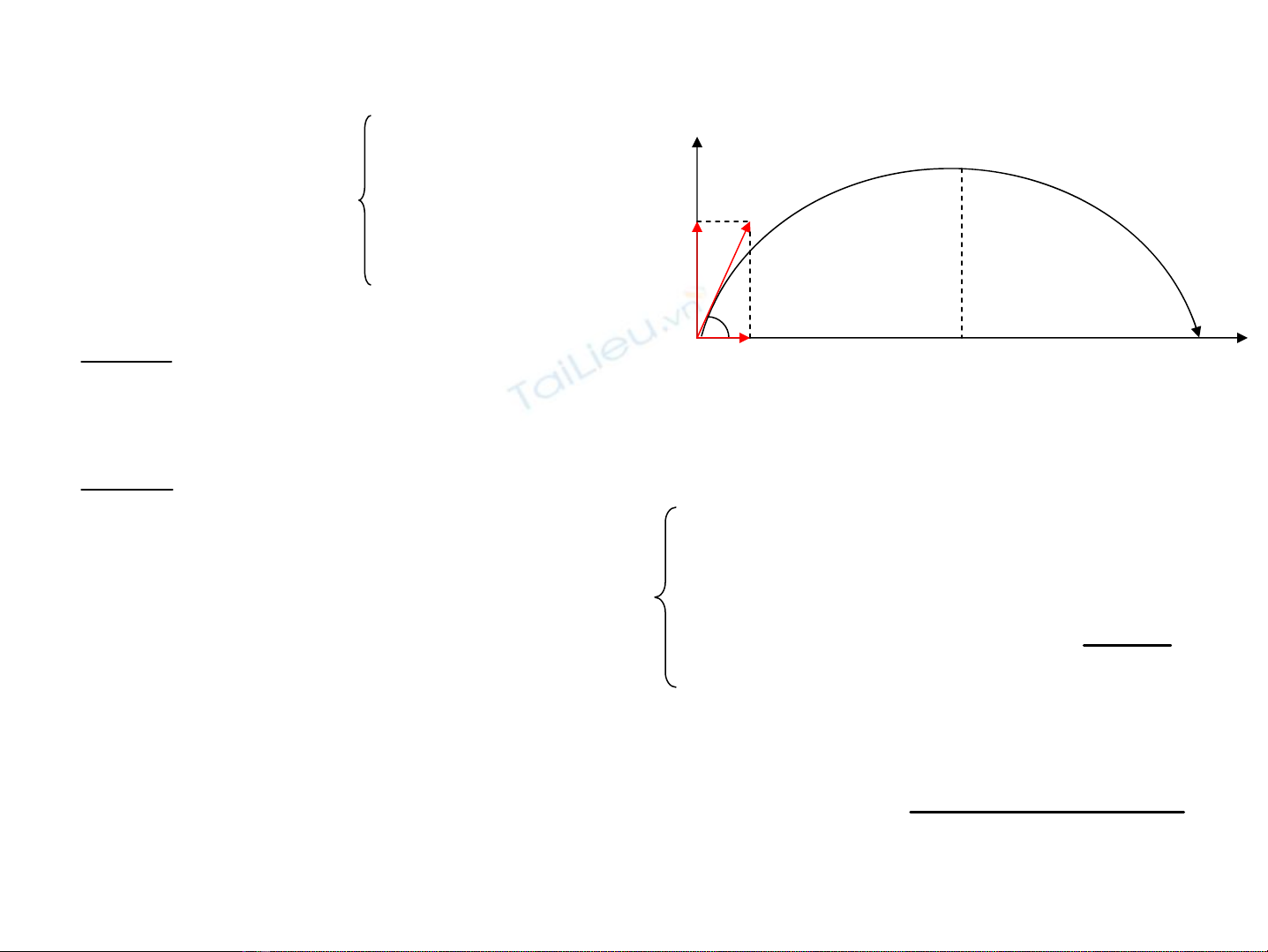
4.3. ChuyÓn ®éng víi gia tèc kh«ng ®æi
Ox
y
hmax
α
0y
v
r
0x
v
r
0
v
r
ax=0
ay=-g
a
r
g
dt
dv
0
y−=
=
dt
dvx
gtsinvv cosv
0y
0−α= α=
x
v
Ph−¬ng tr×nh chuyÓn ®éng
2
gt
t.sinvy
t.cosv 2
0
0
−α=
α
=x
M
Ph−¬ng tr×nh quÜ ®¹o
α
−α= 22
0
2
cosv2
gx
xtgy