intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Cấu trúc dữ liệu: Chương 5 - Cấu trúc dữ liệu cây

Chia sẻ: Lavie Lavie | Ngày: | Loại File: PDF | Số trang:32

Thêm vào BST
Báo xấu
87
lượt xem 4
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Dưới đây là bài giảng Cấu trúc dữ liệu: Chương 5 - Cấu trúc dữ liệu cây. Mời các bạn tham khảo bài giảng để bổ sung thêm kiến thức về định nghĩa; cây nhị phân (cây nhị phân tìm kiếm, cây nhị phân cân bằng). Với các bạn chuyên ngành Công nghệ thông tin thì đây là tài liệu hữu ích.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Cấu trúc dữ liệu: Chương 5 - Cấu trúc dữ liệu cây

  1. Chương 5 Cấu trúc dữ liệu cây
  2. 5.1. Định nghĩa Câ là một Cây ột cấu ấ trúc t ú trong t đó bao b gồm ồ các á nút út được đượ liên kết với nhau theo hệ thống phân cấp, trong đó nút có cấp cao nhất được gọi là nút gốc và nút có cấp thấp nhất được gọi là các nút lá. lá 19/12/2008 Cấu trúc dữ liệu 1 2
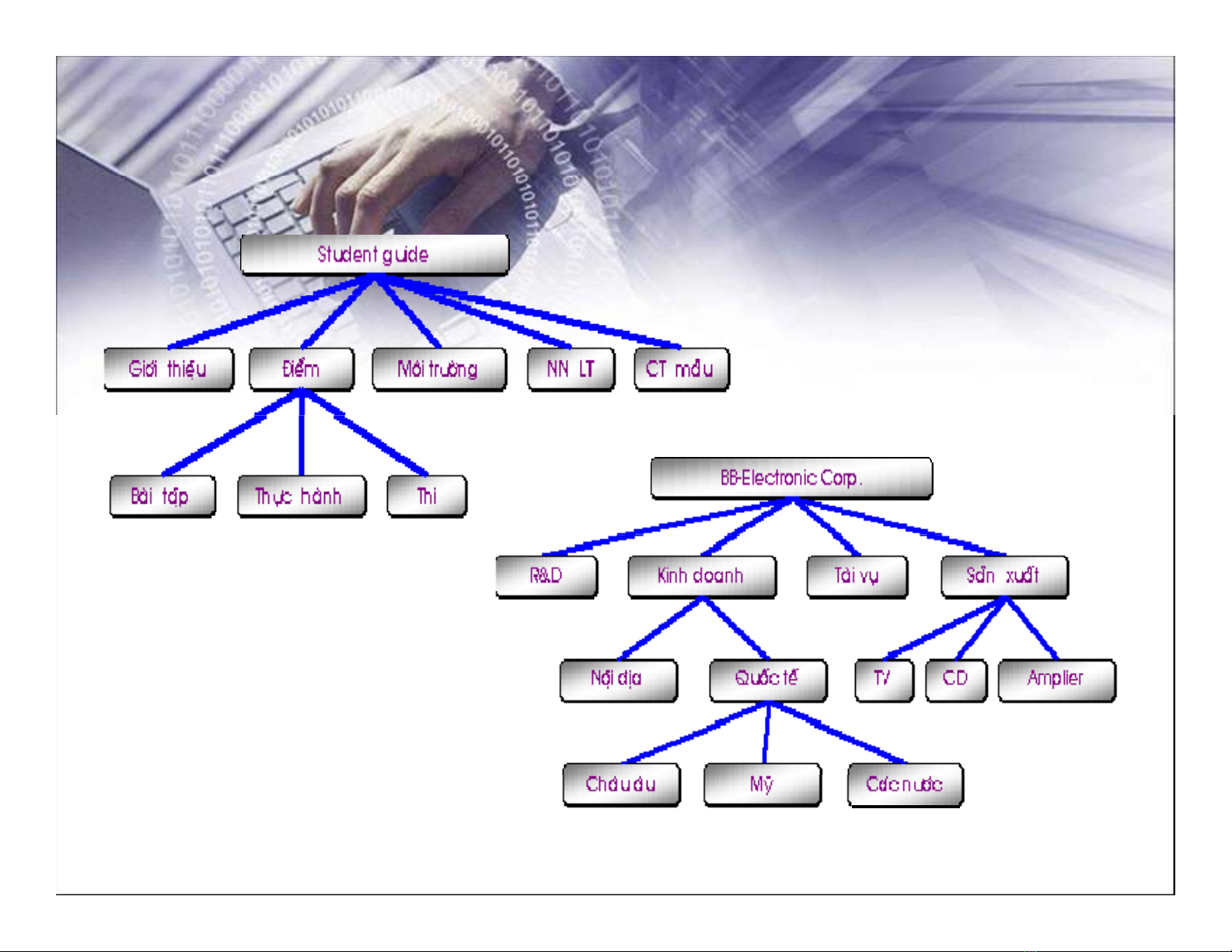
  3. 5.1. Định nghĩa 19/12/2008 Cấu trúc dữ liệu 1 3
  4. 5.1. Định nghĩa • Thuật ngữ: - Nút cha (parents node) của một node là nút có cấp cao hơn nó một bậc. bậc - Nút con (child node) của một node là nút có cấp nhỏ hơn nó một bậc. bậc - Nút gốc (root) là nút không có nút cha. - Nút lá (leaf – leaves) là nút không có nút con. - Cấpp của 1 nút ((level of a node)) là các liên kết để đi từ nút gốc đến nút đó. 19/12/2008 Cấu trúc dữ liệu 1 4
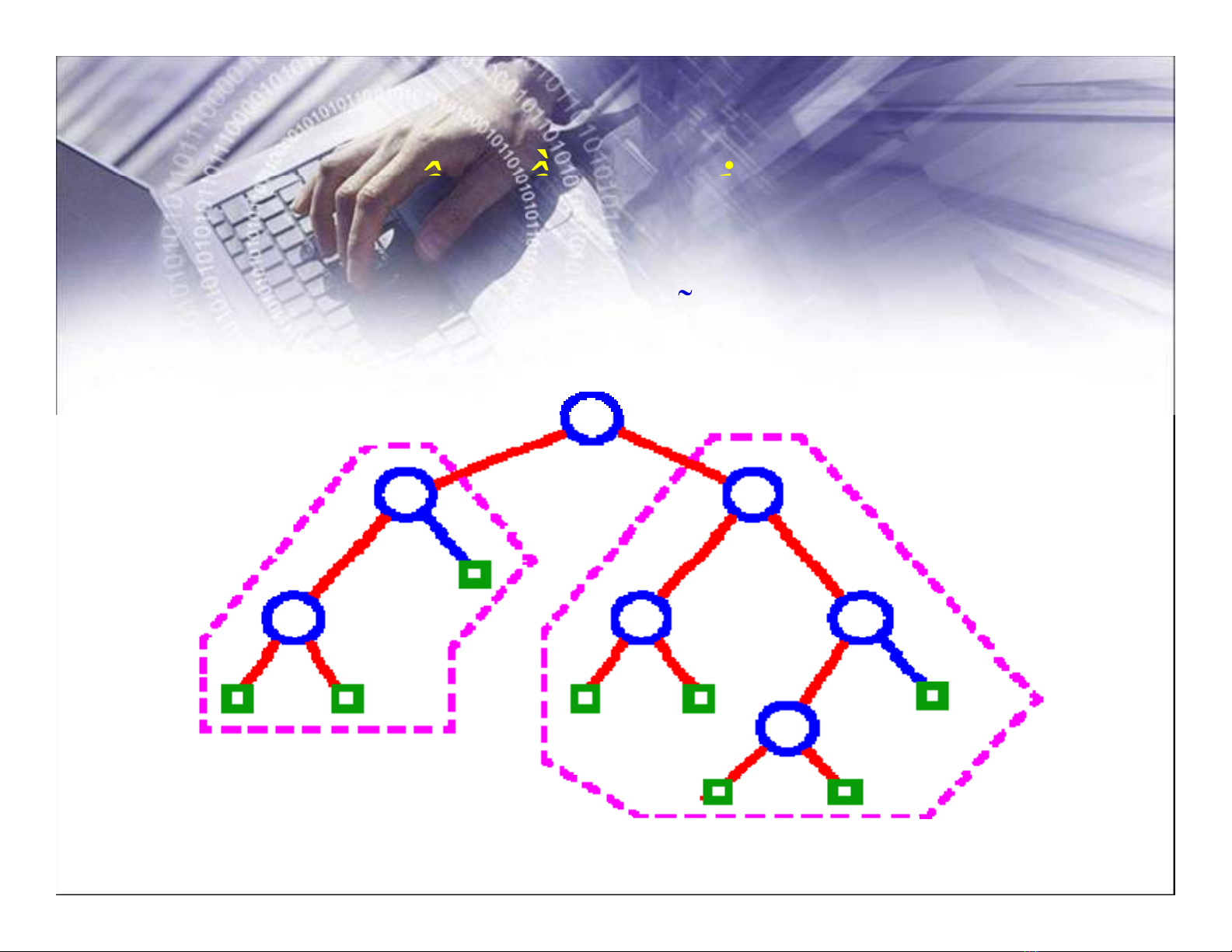
  5. 5.2. Cây nhị phân 5 2 1 Khái niệm về cây nhị phân 5.2.1. Cây nhị phân là một cây mà mỗi ỗ nút có không quá 2 nút con 19/12/2008 Cấu trúc dữ liệu 1 5
  6. 5.2. Cây nhị phân tìm kiếm 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Cây nhị phân tìm kiếm là một cây nhị phân trong đó nút của nó được tổ chức để luôn thỏa tính chất sau đây “Giá Giá trị của nút cha luôn lớn hơn giá trị tất cả nút con bên trái và nhỏ hơn giá trị của tất cả nút con bên phải”. 19/12/2008 Cấu trúc dữ liệu 1 6
  7. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. 19/12/2008 Cấu trúc dữ liệu 1 7
  8. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Biểu diễn cây nhị phân tìm kiếm struct Node { int key; Node * left, * right; }; typedef Node *pNode; struct t t Tree T { pNode root; }; 19/12/2008 Cấu trúc dữ liệu 1 8
  9. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Khởi tạo cây void id Initial iti l (Tree ( &t) t) { t.root = NULL; } Kiểm tra cây rỗng int isEmpty (Tree t) { return (t.root (t root == NULL); } 19/12/2008 Cấu trúc dữ liệu 1 9
  10. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Thêm một nút vào cây Giả sử cần thêm 1 nút có khóa k vào cây t. - So sánh với nút gốc: nếu nhỏ hơn thì sang trái, trái lớn hơn thì sang phải. - So sánh với nút gốc của cây con bên trái (phải) và lặp lại quá trình trên cho đến khi tìm được vị trí thích hợp. 19/12/2008 Cấu trúc dữ liệu 1 10
  11. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Thê một Thêm ộ nút ú vào à cây â int Ins (pNode &r, int k) { if (!r) // //r==NULL { pNode p = new Node; p -> > key = k; p -> left = p -> right = NULL; r = p; return 1; } if (r -> key == k)return 0; if ( (r -> key y > k)) return Ins ( (r->left,k); , ) else return Ins (r->right,k); } 19/12/2008 Cấu trúc dữ liệu 1 11
  12. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Thêm một nút vào cây int i t Insert t (Tree ( &t, t int i t k) { return Insert (t.root,k); } 19/12/2008 Cấu trúc dữ liệu 1 12
  13. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Thêm một nút vào cây int i t Insert t (Tree ( &t, t int i t k) { return Ins (t.root,k); } 19/12/2008 Cấu trúc dữ liệu 1 13
  14. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Tạo cây void CreateTree (Tree &t) { int k; do { cout
  15. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Duyệt cây NLR (Node – Left – Right): 44 18 13 15 37 23 40 88 59 55 71 108 LNR (Left – Node – Right): 13 15 18 23 37 40 44 55 59 71 88 108 LRN (Left – Right – Node): 15 13 23 40 37 18 55 71 59 108 88 44 19/12/2008 Cấu trúc dữ liệu 1 15
  16. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Duyệt cây void LNR (pNode r) { if (!r) return; lnr(r->left); cout
  17. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Tìm khóa k có trong cây hay không int Search(pNode r,int k) { if (!r) return 0; if (r->key == k) return 1; if (r->key > k) return Search(r->left,k); else return Search(r->right,k); } int Search(Tree t,int k) { return Search(t.root,k); } 19/12/2008 Cấu trúc dữ liệu 1 17
  18. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Xóa một nút X - X là nút lá: chỉ đơn giản hủy X vì nó không móc nối đế phần đến hầ tử nào à khác. khá 19/12/2008 Cấu trúc dữ liệu 1 18
  19. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Xóa một nút X - X chỉ có 1 nút con: trước khi hủy X ta móc nối cha của X với ới con duy d nhấthấ của nó. ó 19/12/2008 Cấu trúc dữ liệu 1 19
  20. 5.2. Cây nhị phân 5 2 2 Cây nhị phân tìm kiếm 5.2.2. Các thao tác trên cây nhị phân tìm kiếm Xóa một nút X - X có đủ cả 2 con: không thể hủy trực tiếp do X có đủ 2 con ⇒ hủy gián tiếp.ế Thay vì hủy X, ta sẽ tìm một phần ầ tử thế mạng Y. Phần tử này có tối đa một con. Thông tin l tại lưu t i Y sẽẽ được đ chuyển h ể lên lê lưu l tại t i X. X Sau S đó,đó nút út bị hủy thật sự sẽ là Y giống như 2 trường hợp đầu. Vấn đề là phải chọn Y sao cho khi lưu Y vào vị trí của X,X cây vẫn là CNPTK. Có 2 phần tử thỏa mãn yêu cầu: + Phần tử nhỏ nhất (trái nhất) trên cây con phải. phải + Phần tử lớn nhất (phải nhất) trên cây con trái. 19/12/2008 Cấu trúc dữ liệu 1 20
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
10=>1