1
Chương 2. Hê lực – Force system
Chương
2
Cơ học kỹ thuật: TĨNH HỌC
Engineering Mechanics: STATICS
Hệ lực
Nguyễn Quang Hoàng
Bộ môn Cơ học ứng dụng
Chương 2. Hê lực – Force system -2-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Nội dung
1. Biểu diễn véc tơ lực, tổng hợp các lực cùng điểm
đặt, phân tích lực thành nhiều thành phần, véc tơ
chính của hệ lực.
2. Mô men của lực đối với một điểm / một trục, mô men
chính của hệ lực.
3. Ngẫu lực, ngẫu lực tương đương, thu gọn hệ ngẫu
lực, phân tích ngẫu lực.
4. Thu gọn hệ lực, các dạng chuẩn, thu gọn hệ lực
phân bố song song.
Chương 2. Hê lực – Force system -3-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
VÉC TƠ VỊ TRÍ VÀ VÉC TƠ LỰC
1. Vô hướng và véc tơ
2. Véc tơ vị trí
3. Nhắc lại một số phép tính véc tơ
4. Véc tơ lực
5. Tổng hợp và phân tích lực
6. Véc tơ chính của hệ lực
2
Chương 2. Hê lực – Force system -4-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Đại lượng vô hướng và đại lượng véc tơ
Vô hướng: đại lượng đặc trưng bởi một số dương hoặc âm. Ví dụ khối
lượng, thể tích, diện tích, nhiệt độ.
,,, ,...rvaF

()ijk

[]
T
xyz
aaaa
xyz
aaiajak

Véc tơ: đại lượng có cả độ lớn và hướng. Ví dụ vị trí, lực, mô men, vận
tốc, gia tốc. Véc tơ được biểu diễn bằng đoạn thẳng có hướng
,,,,...mAVT
Khi tính toán: đưa vào hệ trục tọa độ với các
véc tơ đơn vị ()
xyz
eee

hoặc
véc tơ đại số.
véc tơ hình học
x
y
z
ij
k
ay
ax
aza
222
xyz
a aaa Độ lớn hay độ dài
của véc tơ.
Chương 2. Hê lực – Force system -5-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Véc tơ trong không gian 3D
FFu=
O
A
B
x
y
z
u
,||1FFu u==

Biểu diễn thông qua véc tơ đơn vị
cos cos cos /uijkaaabg=++=
x
e
y
e
z
e
x
ay
a
z
aa
x
y
z
Biểu diễn trong tọa độ Đề-các vuông góc
xyz
aaiajakau=++=


22 2 2
cos cos cos 1uabg=++=
1[ , , ] [cos , cos , cos ]
TT
xyz
aaaa

u
11
1
cos ( / ), cos ( / ),
cos ( / )
xy
z
aa aa
aa



222
xyz
aaaa
Chương 2. Hê lực – Force system -6-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Véc tơ trong không gian 2D
xy
FFiFj

22
() ()
xy
FF F F
Độ lớn
Hướng - Véc tơ chỉ phương, (đơn vị)
1[ , ] [cos , cos ] [cos , sin ]
TTT
xy
FFF

 u
T
[, ]
xy
FFF
/xy
uFFuiuj

x
y
i
jFx
Fy
F
x
y
F
x
F
y
Fb
a
c
y
xF
FF
abc
==
,
xy
ab
FFFF
cc
= =
3
Chương 2. Hê lực – Force system -7-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Biểu diễn véc tơ nối hai điểm
x
e
y
e
z
e
a
d
b
O
A
B
222
()()()
||
()()()
()()()
,,,
BAx BAy BAz
BA BA BA
BAx BAy BAz
BA BA BA
xyz
dABba
xxe yye zze
dAB
xx yy zz
xxe yye zze
d
udd
xx yy zz
uuu
ddd
==-
=- +- +-
=
=-+-+-
-+-+-
==
---
===





(, , )
AAA Ax Ay Az
Axyz axeyeze= + +

(, , )
BBB Bx By Bz
Bx y z b xe ye z e= + +

Chương 2. Hê lực – Force system -8-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Các phép tính trên véc tơ hình học
Cộng (trừ) hai véc tơ
Tích vô hướng hai véc tơ
cab=+

a
b
c
a
b
c
||||cos(,)||||cosab ab ab ab baa⋅= = =⋅

 a
b
()caba b=-=+-


,
right hand rule
||||.||sin
0,
cacb
cab
cab
ab c ab b a
a
ì
ï^^
ï
ï
ï
ï
=´ í
ï
ï
ï=
ï
ï
î
= ´=-´





a
b
c
Tích có hướng
Chương 2. Hê lực – Force system -9-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Một số phép tính véc tơ
()()()
xxx yyy zzz
ab a be a be a be= + +

Trong hệ trục tọa độ (Oxyz), với các véc tơ đơn vị {, , }
xyz
eee

xx yy zz
ab ab ab ab ba⋅= + + =⋅


,,
xx yy zz xx yy zz
aae ae ae bbe be be=++ =++
 
()
() ,
()
xyz yz zyx
xyz zx xzy xx yy zz
xyz xy yxz
eee ababe
cab aaa ababe ce ce ce
bbb ababe
æö
-+
÷
ç÷
ç÷
ç÷
ç
=´= = - += + +
÷
ç÷
ç÷
ç÷
-÷
ç
èø


0
0
0
xyzzy zyx
yzxxz z xy
zxyyx yx z
cabab aab
cabab a ab
cabab aa b
éù é ù é ùéù
--
êú ê ú ê úêú
êú ê ú ê úêú
=-= - =
êú ê ú ê úêú
êú ê ú ê úêú
--
êú ê ú ê úêú
ëû ë û ë ûëû
cab
4
Chương 2. Hê lực – Force system -10-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Tổng hợp hệ lực đồng qui và phân tích lực
F12
F2
F1
A
F3
R
Tổng hợp hệ lực đồng qui
•Hệlựcđồng qui: các lực cùng đi qua một điểm
• Tổng hợp hệ lực đồng qui ta thu được một lực đặt tại điểm đồng qui.
Áp dụng tiên đề
hình bình hành lực Nối liên tiếp các véc
tơ lực thành phần
(đa giác lực)
F2
F1
A
F3
R
F2
F1
A
F3
123
FFF R++=

Chương 2. Hê lực – Force system -11-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Phân tích lực thành nhiều thành phần
F
a
b
a
b
F
a
F
b
F
F12
F2
F1
A
F3
R
•Ngượcvớitổng hợplực, mộtlựccóthểđược phân tích thành tổng của
nhiềulực cùng đặttạimộtđiểm.
123
RFF F=++

ab
FFF=+

Chương 2. Hê lực – Force system -12-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
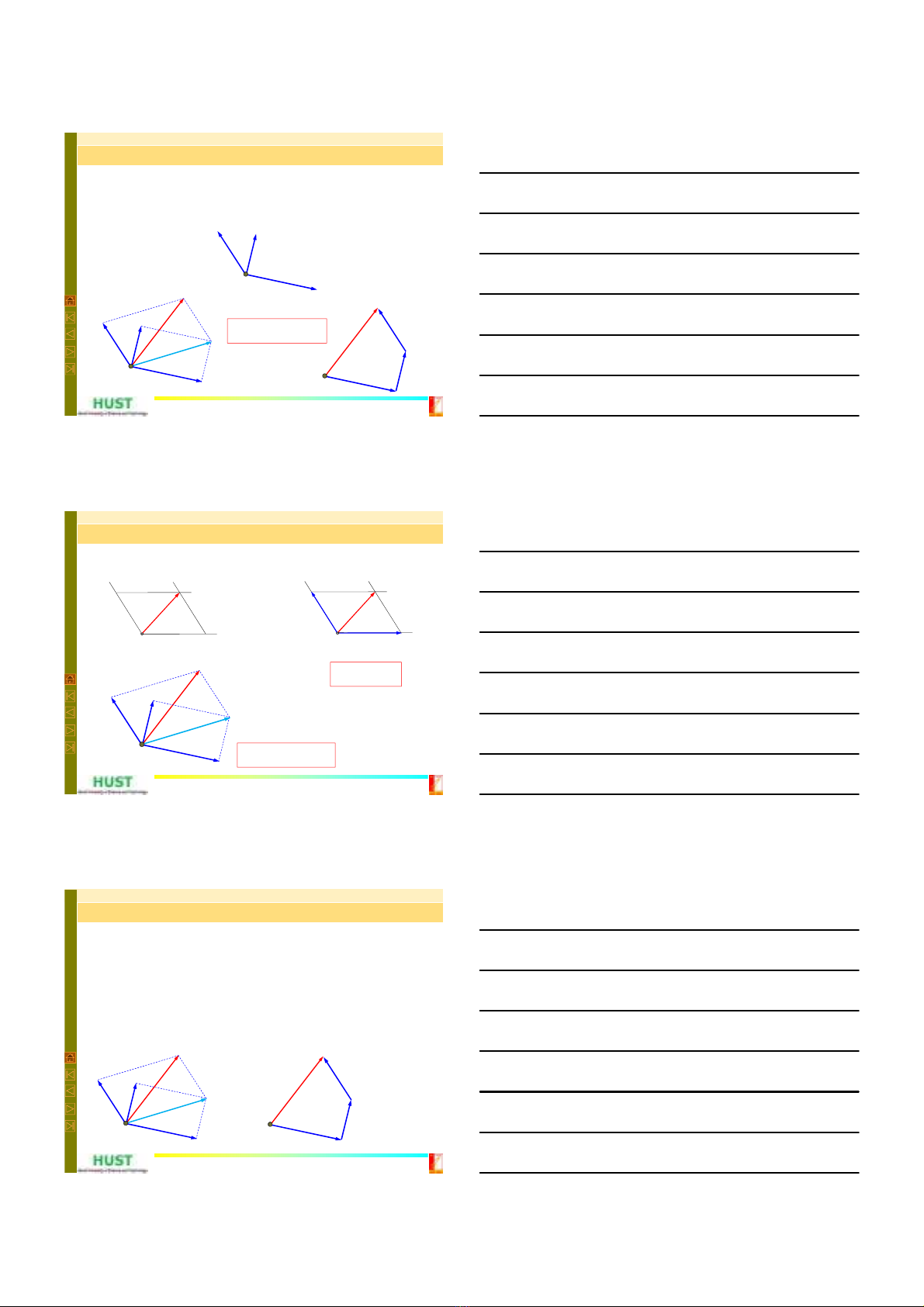
Véc tơ chính của hệ lực
Véc tơ chính của hệ lực là tổng hình học các véc tơ lực của
hệ lực.
12
1
...
n
Rnk
k
FFF F F


Phương pháp vẽ (qui tắc hình bình hành & vẽ nối tiếp các véc tơ
lực)
Xác định véc tơ chính
F12
F2
F1
A
F3
FR
F2
F1
A
F3
FR
đa giác lực:
phẳng hoặc
ghềnh
5
Chương 2. Hê lực – Force system -13-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Véc tơ chính của hệ lực
Phương pháp hình chiếu, sử dụng hệ trục tọa độ đề các
x
e
y
e
z
e
2
F
1
F
n
F
O
R
F
12
1
(, ,..., ),
, ( 1,2,..., )
n
nRk
k
kkxxkyykzz
FF F F F
FFeFeFe k n



222
RRxRyRz
F FFF
222
/Rx x Ry y Rz z
RR
Rx Ry Rz
Fe Fe Fe
uFF
FFF




,
(), (), ()
RRxxRyyRzz
Rx kx Ry ky Rz kz
FFeFeFe
FFFFFF

  

RR
FFu
Chương 2. Hê lực – Force system -14-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
Ví dụ
Tổng hợp hai lực cho trong mặt phẳng như trên hình.
22 22
22
22
12
1
12 5
2512 512
12
512
5
512
200 sin 30 200 cos 30 0
260 260 0
( ) 200 sin 30 260 ..
( ) 200 cos 30 260 ..
()0
R
xyz
xyz
Rx kx
Ry ky
Rz kz
FFF
Feee
Feee
FF
FF
FF










RRxxRyyRzz
FFeFeFe

222
RRxRyRz
FFFF
y
x
F1, 200 N
F2, 260 N
512
30o
y
x
F1, 200 N
F2, 260 N
512
30o
F1x
F1y
F2y
F2x
Chương 2. Hê lực – Force system -15-
Nguyễn Quang Hoàng - Department of Applied Mechanics-SME
MÔ MEN CỦA LỰC ĐỐI VỚI
MỘT ĐIỂM – ĐỐI VỚI MỘT TRỤC
1. Biểu diễn mô men dạng véc tơ
2. Biểu diễn mô men dạng vô hướng / mô
men đại số
3. Mô men của lực đối với một trục
4. Mô men chính của hệ lực