Cơ học lý thuyết
1. Tài liệu học tập học phần Cơ Học Lý Thuyết. HUTECH
2. Cơ học tập 1, tập 2, Đỗ Sanh.
3. Engineering Mechanics Statics, Dynamics. Hibbeler,
2016.
Cơ học lý thuyết
Phần 1
TĨNH HỌC
Phần 2
ĐỘNG HỌC
Phần 3
ĐỘNG LỰC HỌC
Môn học nghiên cứu các quy luật tổng quát của
chuyển động,cân bằng của vật rắn và sự
tương tác của chúng với nhau.
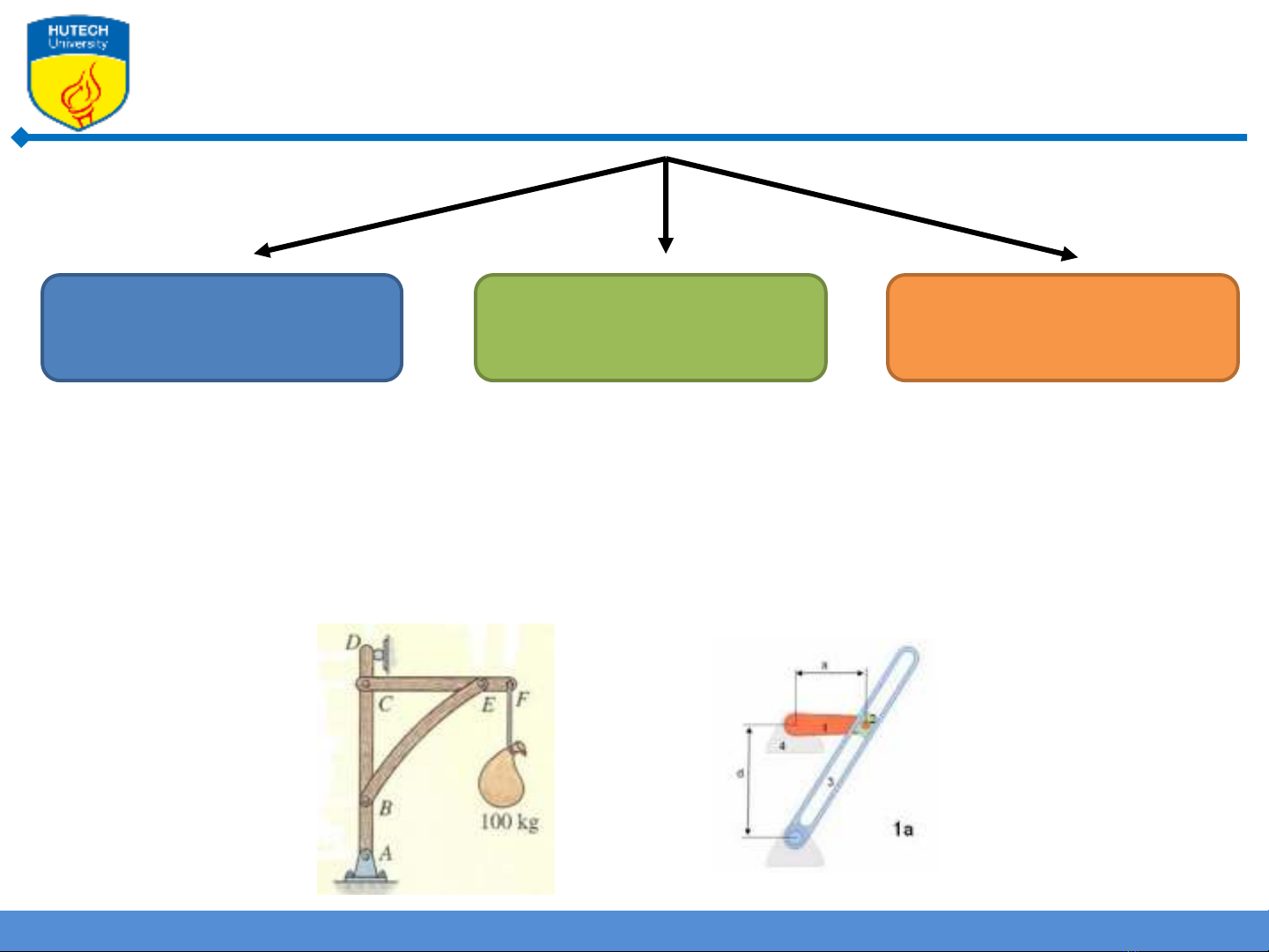
Tĩnh học
Phần 1
TĨNH HỌC
LỰC MOMENT
Cân bằng
Nghiên cứu sự tương tác giữa các vật trong
kết cấu chịu lực đang cân bằng
Xác định lực căng dây
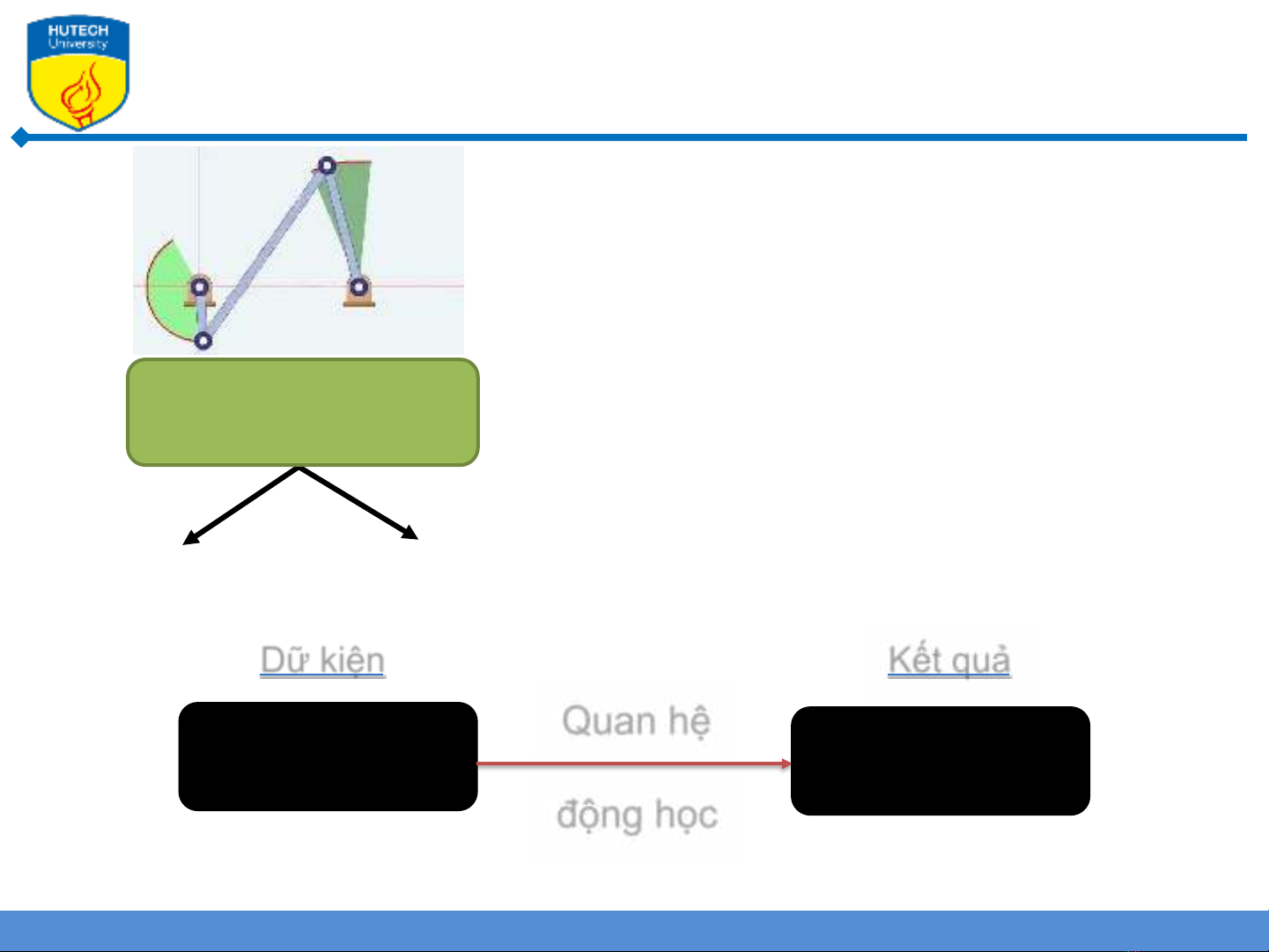
Vận tốc Gia tốc
Vị trí, vận tốc,
gia tốc vật 1
Dữ kiện
Quan hệ
động học
Vị trí, vận tốc,
gia tốc vật 2
Kết quả
Phần 2
ĐỘNG HỌC
Xác định tất cả các đại lượng
động học (vị trí, vận tốc, gia tốc)
đặc trưng cho chuyển động của
vật mà không quan tâm đến
nguyên nhân gây ra chuyển
động.
Động học
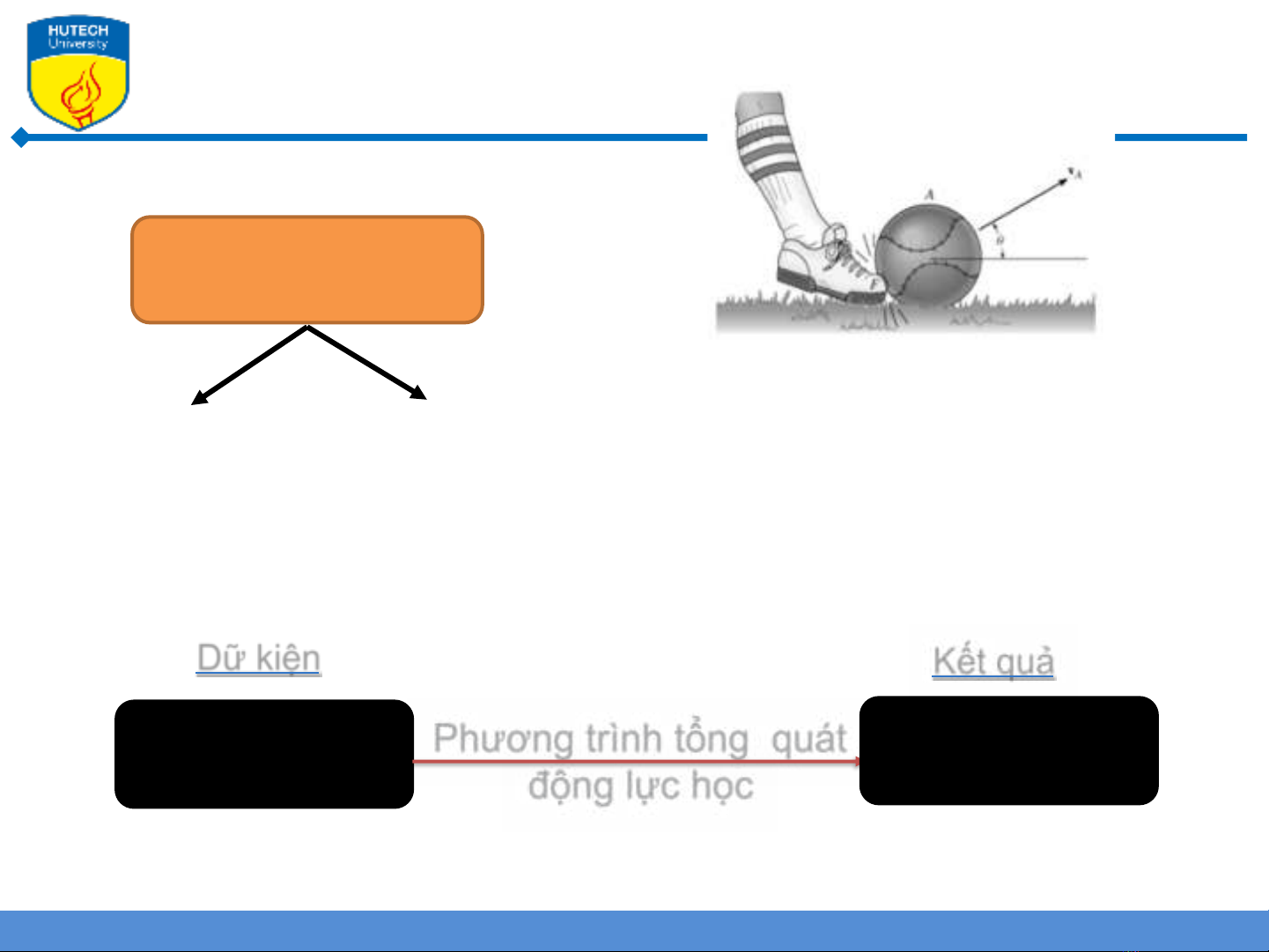
Phương trình tổng quát
động lực học
Lực
Moment Vận tốc
Gia tốc
Lực
Moment
Dữ kiện
Vận tốc, gia tốc
Phản lực liên kết
Kết quả
Khảo sát các quy luật chuyển
động của vật thể dưới tác dụng
của lực.
Phần 3
ĐỘNG LỰC HỌC
Vận tốc trái banh khi tác
dụng lực
Động lực học