Phần I
TĨNH HỌC
Chương 1: Các khái niệmcơbản, mô hình phảnlực liên kết
Chương 2: Thu gọnhệlực, điềukiện cân bằng
Chương 3: Các bài toán đặcbiệt
Chương 4: Ma sát
Bộ môn Cơ Kỹ thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa Tp.HCM
Chương 5: Trọng tâm
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
Chương 2. Thu gọn hệ lực và Điều kiện cân bằng của hệ lực
Bộ môn Cơ Kỹ thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa Tp.HCM
NỘI DUNG
2.2. Các định lý cơbảncủatĩnh học
2.4. Các dạng chuẩncủahệlực(dạng tốigiản)
Chương 2
Thu gọn hệ lực và Điều kiện cân bằng của hệ lực
2.1. Hai thành phầncơbảncủahệlực
2.3. Điềukiện cân bằng củahệlực
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
Chương 2. Thu gọn hệ lực và Điều kiện cân bằng của hệ lực
Bộ môn Cơ Kỹ thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa Tp.HCM
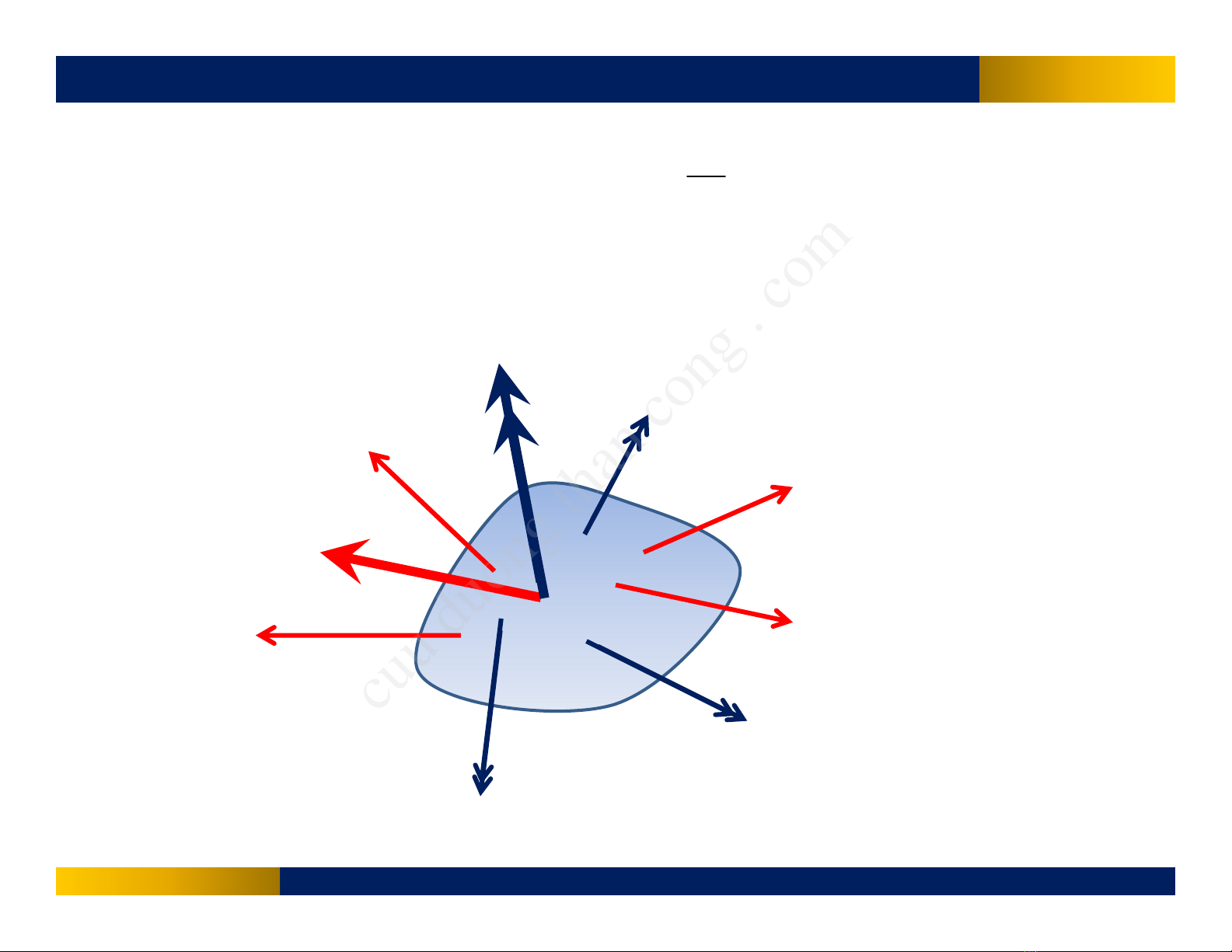
Khảosátmộthệcó nhiềulực
2.1. Hai thành phầncơbảncủahệlực
;1,
j
F
jn
Mộthệlựcluôncó2thànhphầncơbảnlàvector chính và vector
moment chính:
P3
P1
P2
Pn
M1
M2
Mm
MO
RO
O
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
Chương 2. Thu gọn hệ lực và Điều kiện cân bằng của hệ lực
Bộ môn Cơ Kỹ thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa Tp.HCM
2.1. Hai thành phầncơbảncủahệlực
Vector chính của một hệ nhiều lực là vector tổng của tất cả các
vector lực trong hệ.
Vector chính
1
xj
x
n
jy jy
j
z
j
z
RF
RFR F
RF
Vector chính Thành phầncơbảnthứnhấtcủamộthệlực
Tính chất:
-Đốivới1hệlựcxácđịnh, vector chính củahệlựcđólàvectorhằng gọilà
bấtbiếnthứnhấtvớihệlựcđó.
-Vector chính củamộthệlựclàmộtvectortựdo, có thểnằmtrênđường
tác dụng song song tùy ý trong không gian tồntạicủahệlực.
CuuDuongThanCong.com https://fb.com/tailieudientucntt
cuu duong than cong . com
