GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 332
Chương 5
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 334
O
z
x
y
r
z
1
y
1
x
1
O
1
r
0
r
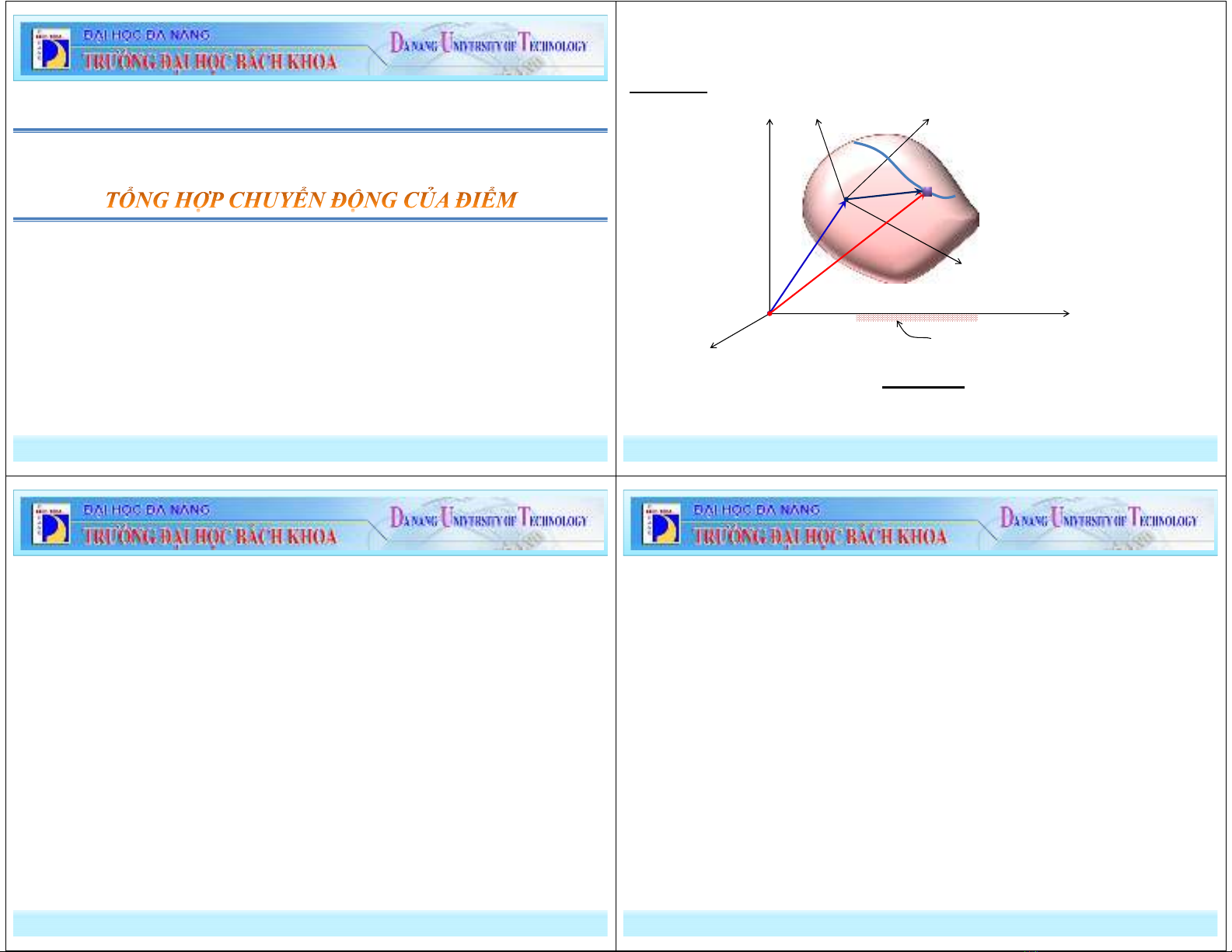
Hệ quy chiếu cố định
M
* Vật rắn (S) chuyển động trong hệ quy chiếu cố định (Oxyz).
* Chất điểm M chuyển động trên vật rắn (S)
Yêu cầu: Tìm vận tốc và gia tốc của điểm M trong hệ trục cố định Oxyz.
* Chọn hệ quy chiếu (O1x1y1z1) gắn cứng trên vật rắn (S). O1x1y1z1: là hệ
quy chiếu động.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 333
§1. Nội dung bài toán
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 335
§2. Các loại chuyển động
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 336
1 1 1 1 1 1 1 1
. . .
O M r x i y j z k
= = + +

1 1 1
, , :
i j k
các véc tơ đơn vị lần lượt ứng với 3 trục x1, y1, z1,
là các hằng số trong hệ trục O1x1y1z1
a. Véc tơ định vị
5.1
1. Chuyển động tương đối: M/O1x1y1z1
Trong hệ trục tọa độ O1x1y1z1:
+ Phương trình chuyển động tương đối được ký hiệu:
+ Vận tốc tương đối được ký hiệu:
+ Gia tốc tương đối được ký hiệu:
( )
r r
s s t
=
r
v
r
a
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 338
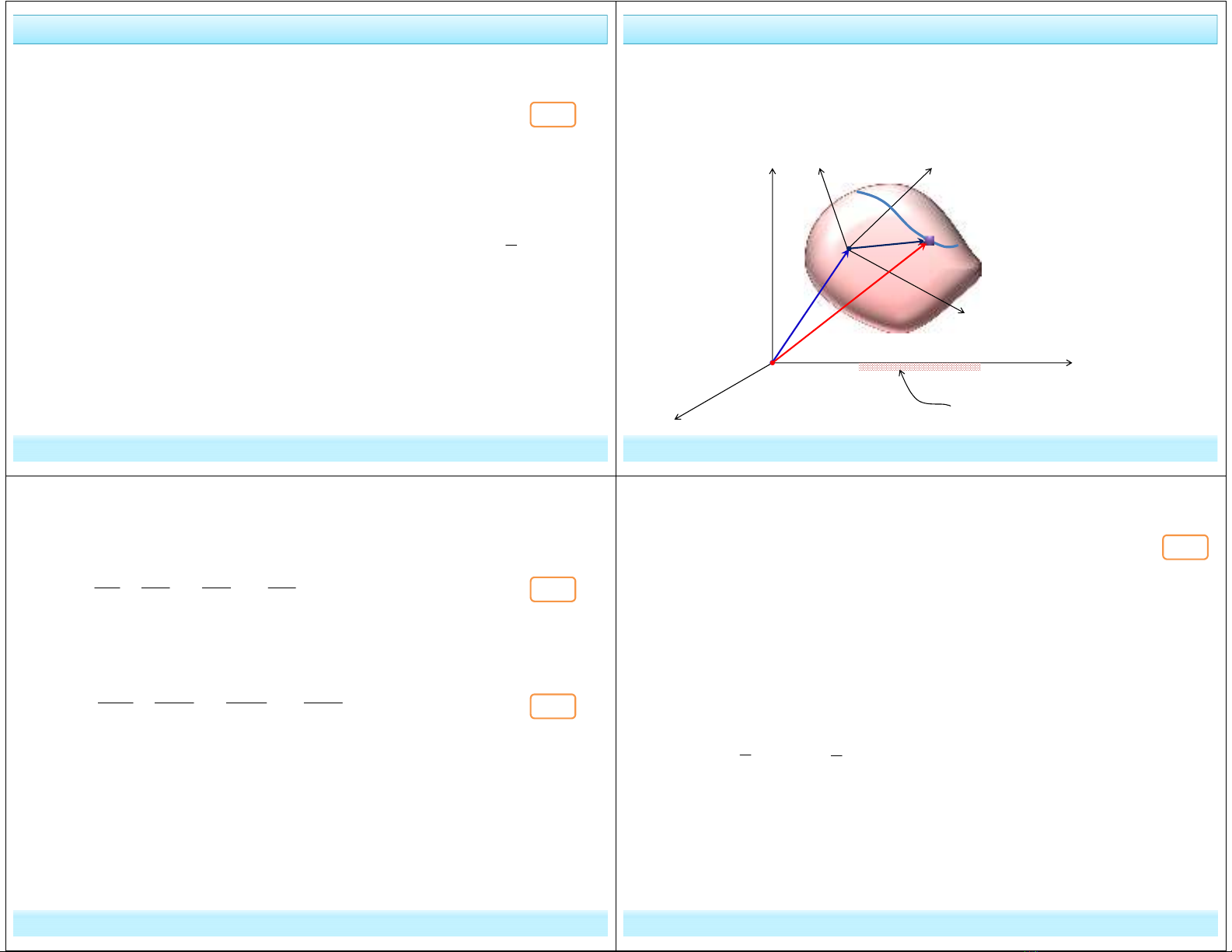
Tưởng tượng dừng chuyển động tương đối của M đối với vật rắn (S)
(điểm M* định vị vị trí dừng – gọi là trùng điểm), lúc này chuyển động
của M* so với hệ trục cố định Oxyz được gọi là chuyển động theo của
điểm M.
O
z
x
y
e
r
z
1
y
1
x
1
O
0
r
Hệ quy chiếu cố định
*
M
2. Chuyển động kéo theo: O1x1y1z1 / Oxyz
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 337
b. Vận tốc tương đối
1 1 1 1
1 1 1
r
dr dx dy dz
v i j k
dt dt dt dt
= = + +
2 2 2 2
1 1 1 1
1 1 1
2 2 2 2
r
d r d x d y d z
a i j k
dt dt dt dt
= = + +
c. Gia tốc tương đối
5.2
5.3
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 339
* *
1 1 0 1 1 1 1 1 1
. . .
e
r OM OO O M r x i y j z k
= = + = + + +
 

a. Véc tơ định vị
1 1 1
, , :
x y z
là các hằng số trong hệ trục Oxyz
1 1 1
, , :
i j k
các véc tơ đơn vị lần lượt ứng với 3 trục x1, y1, z1,
là đại lượng thay đổi theo t trong hệ trục Oxyz
5.4
Trong hệ trục tọa độ Oxyz:
+ Phương trình chuyển động theo được ký hiệu:
+ Vận tốc theo được ký hiệu:
+ Gia tốc theo được ký hiệu:
( ), ( )
e e e e
t s s t
ϕ ϕ
= =
e
v
e
a
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 340
b. Vận tốc theo
0
1 1 1
1 1 1
. . .
e
e
dr dr
di dj dk
v x y z
dt dt dt dt dt
= = + + +
c. Gia tốc theo
2 2 2 2 2
0
1 1 1
1 1 1
2 2 2 2 2
. . .
e
e
d r d r
d i d j d k
a x y z
dt dt dt dt dt
= = + + +
5.5
5.6
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 342
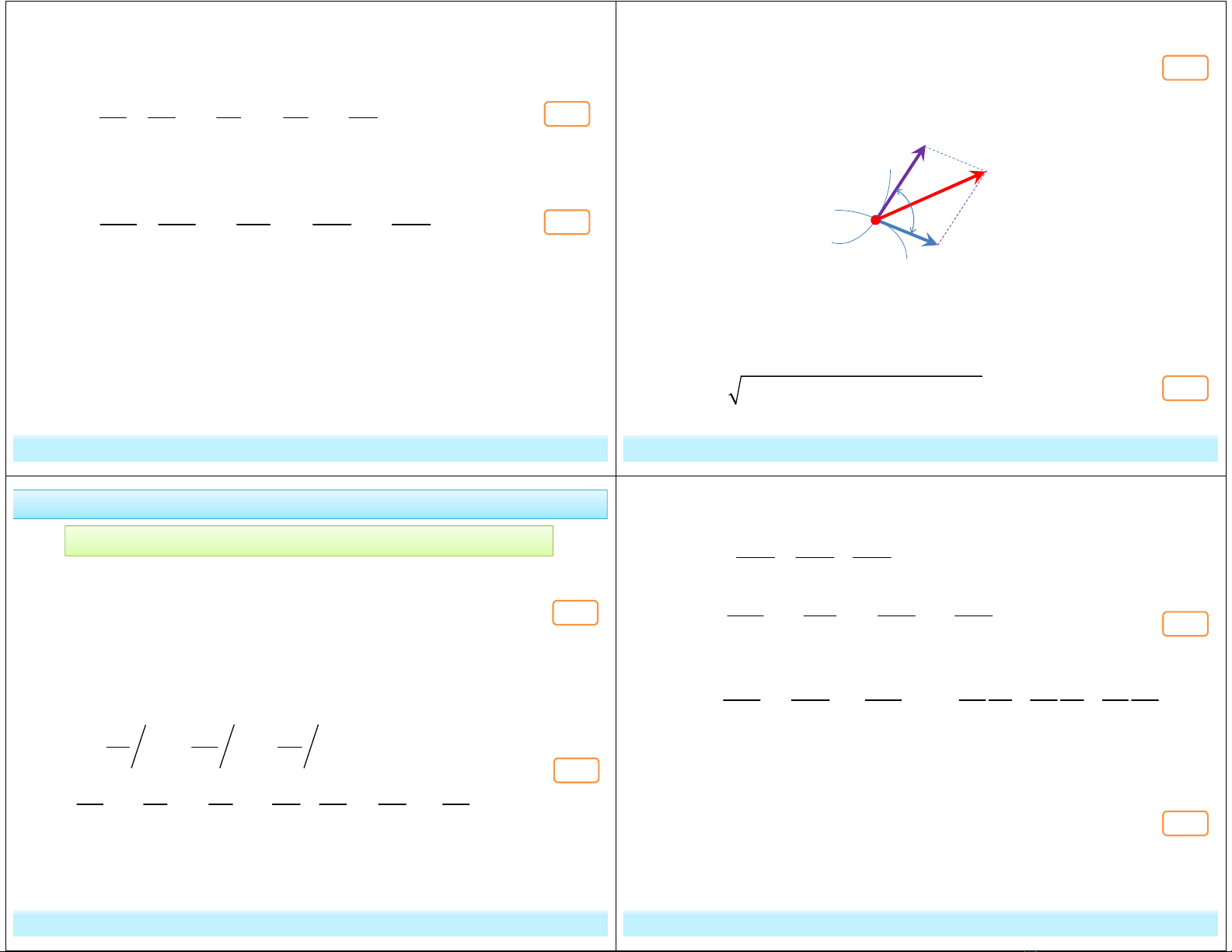
2 2
( ) ( ) 2. .cos
M M M M M
a e r e r
v v v v v
α
= + +
M M M
a e r
v v v
= +
* Công thức véc tơ
* Công thức tính độ lớn
5.9
5.10
M
r
v
M
e
v
M
a
v
M
qđ (r)
qđ (e)
α
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 341
1 1 0 1 0 1 1 1 1 1 1
. . .
r OM OO O M r r r x i y j z k
= = + = + = + + +
  
Chuyển động tuyệt đối = CĐ kéo theo + CĐ tương đối
a. Véc tơ định vị
1 1 1 1 1 1
, , , , , :
x y z i j k
là các đại lượng thay đổi theo t trong hệ trục Oxyz
b. Vận tốc tuyệt đối của M – Định lý hợp vận tốc
01
01 1 1 1 1 1
1 1 1 1 1 1
. . .
e r
M
a Oxyz Oxyz Oxyz
v v
dr dr
dr
vdt dt dt
dr
di dj dk dx dy dz
x y z i j k
dt dt dt dt dt dt dt
= = +
= + + + + + +
 
5.7
5.8
3. Chuyển động tuyệt đối: M / Oxyz
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 343
c. Gia tốc tuyệt đối của M – Định lý hợp gia tốc
M M
M
Ma e
r
a
dv dv
dv
a
dt dt dt
= = +
22 2 2
0
1 1 1
1 1 1
2 2 2 2
. . .
M
e
a
d r
d i d j d k
x y z
dt dt dt dt
= + + +

2 2 2
1 1 1 1 1 1 1 1 1
1 1 1
2 2 2 2
MM
r
c
aa
d x d y d z dx di dy dj dz dk
i j k
dt dt dt dt dt dt dt dt dt
+ + + + + +


* Công thức véc tơ gia tốc tuyệt đối
M M M M
a e r c
a a a a
= + +
5.11
5.12
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 344
r
a
τ
T
e
a
M
T
N
N
e
a
τ
n
n
r
a
c
a
qđ (r)
qđ (e)
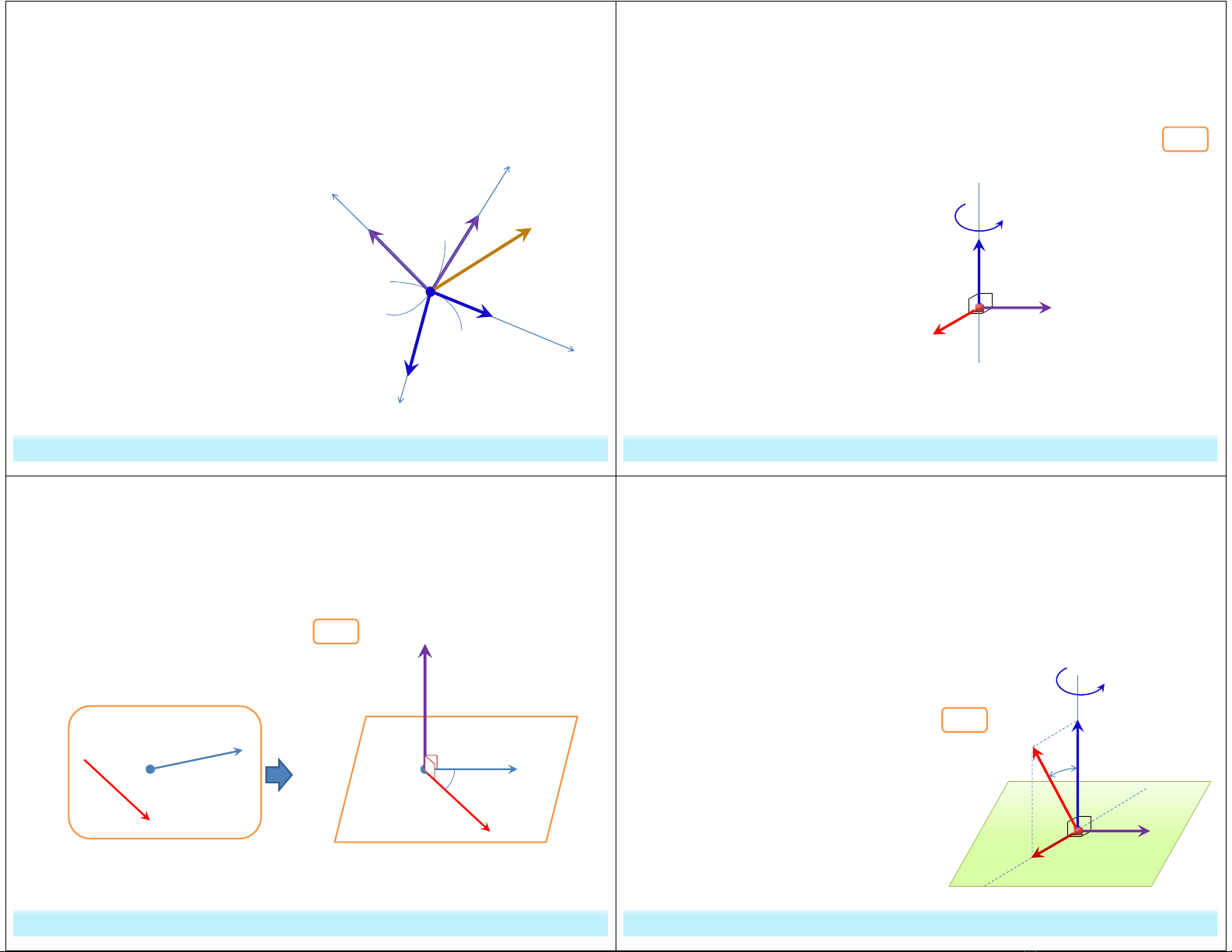
Khi thực hành:
- Trong mặt phẳng mật tiếp của quỹ đạo tương đối (r), gán hệ trục M
τ
n.
- Trong mặt phẳng mật tiếp của quỹ đạo theo (e), gán hệ trục M
Τ
N.
Công thức gia tốc trở thành:
M n T N
a r r e e c
a a a a a a
τ
= + + + +
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 346
- Khi M chuyển động trong một mặt phẳng thì
+ Chiều của xác định bởi
+ Độ lớn:
e r
v
ω
⊥
2. .
c e r
a v
ω
=
* Cách xác định véc tơ gia tốc Coriolis
c
a
c
a
( , , )
r c e
v a
ω
là tam diện thuận
5.14
e
ω
c
a
r
v
e
ω
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 345
* Gia tốc Coriolis
c
a
+ Khi hệ quy chiếu động O1x1y1z1
chuyển động quay quanh một trục
cố định ∆ với vận tốc góc là thì:
e
ω
2.
c e r
a v
ω
= ∧
Khi hệ quy chiếu động chuyển động tịnh tiến thì nên
0
c
a
=
0
e
ω
=
2. . .sin( , ) 2. . .sin
c e r e r e r
a v v v
ω ω ω α
= =
5.13
M
r
v
e
ω
M
r
v
e
ω
c
a
α
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 347
- Khi M không chuyển động trong một mặt phẳng:
*
( , , )
r c e
v a
ω
+ Trong mặt phẳng : chiếu lên mặt phẳng vuông góc với
được .
+ Xoay theo chiều quay của một góc 900 sẽ được phương và
chiều của , với là tam diện thuận.
( , )
e r
v
ω
r
v
e
ω
*
r
v
*
r
v
e
ω
c
a
*
2. . 2. . .sin
c e r e r
a v v
ω ω α
= =
+ Độ lớn:
5.15
e
ω
c
a
*
r
v
r
v
α
e
ω
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 348
BÀI TẬP CHƯƠNG 5 SINH VIÊN CẦN GIẢI QUYẾT
Tổng hợp chuyển động của điểm có hai dạng bài toán
-Bài toán thứ nhất: Tổng hợp chuyển động.
-Bài toán thứ hai: Phân tích chuyển động.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 350
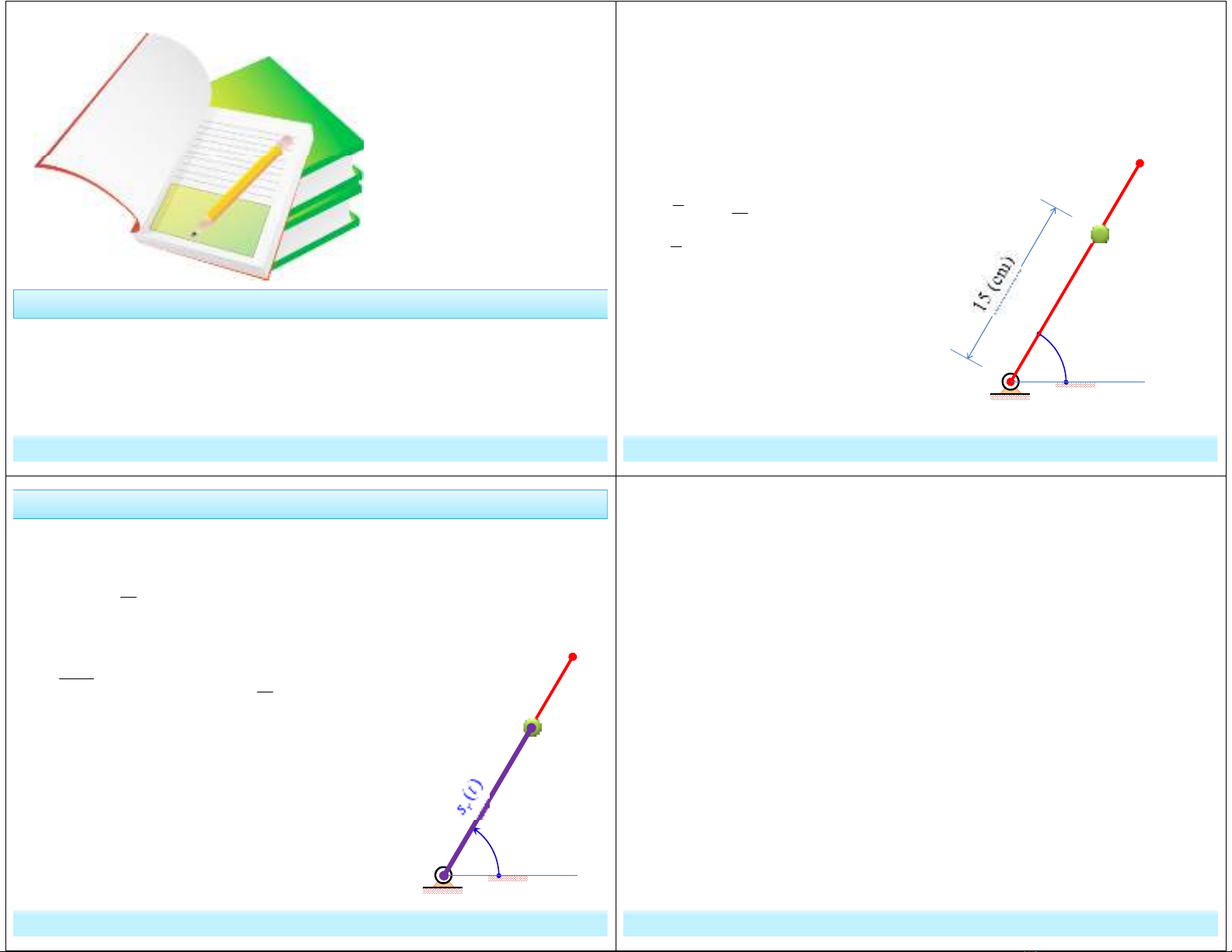
Khi t = 1(s):
* Phân tích chuyển động:
- Chuyển động M trên thanh thẳng AB là chuyển động tương đối
- Chuyển động quay của thanh AB quanh A cố định mang M
chuyển động theo
* Định vị trí của M:
(1) (rad) 0
3
(1) 15 (cm) 0
e
r
s
π
ϕ
= >
= >
Vị trí của M xác định như hình vẽ
0
60
B
A
M
* Để ý rằng: chuyển động của M trong
bài toán này là kết hợp từ 2 chuyển
động trong các Bài tập 3.2 và 4.2.
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bôSlide 349
Cho thanh AB = 20 (cm) quay trong một mặt phẳng xác
định quanh điểm A cố định, với phương trình quay:
Chất điểm M chuyển động trên đường đoạn thẳng AB với
phương trình:
Khi t = 1 (s), xác định:
+ Vị trí của M.
+ Vận tốc tuyệt đối của M.
+ Gia tốc của tuyệt đối của M.
( ) 10.(1 sin ) (cm)
6
r
AM s t t
π
= = +
Bài tập 5.1
( )
e
t
ϕ
B
A
M
2
( ) ( 1) (rad)
3
et t t
π
ϕ
= + −
GV Huỳnh Vinh – ĐHBK Đà Nẵng Lưu hành nội bô Slide 351
* Gán các hệ trục tọa độ:
. Tại M trên quỹ đạo tương đối của M gán trục tọa độ theo chiều
dương của quỹ đạo tương đối (r) của M
M
τ
:
:
T
MTN
N
Tiếp tuyến quỹ đạo theo của M theo chiều quay của (AB)
Hướng về tâm cong quỹ đạo theo của M
. Tại M trong mặt phẳng mật tiếp của quỹ đạo chuyển động theo (e)
gán hệ trục tọa độ: