Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011
Giảng viên Nguyễn Duy Khương 1
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
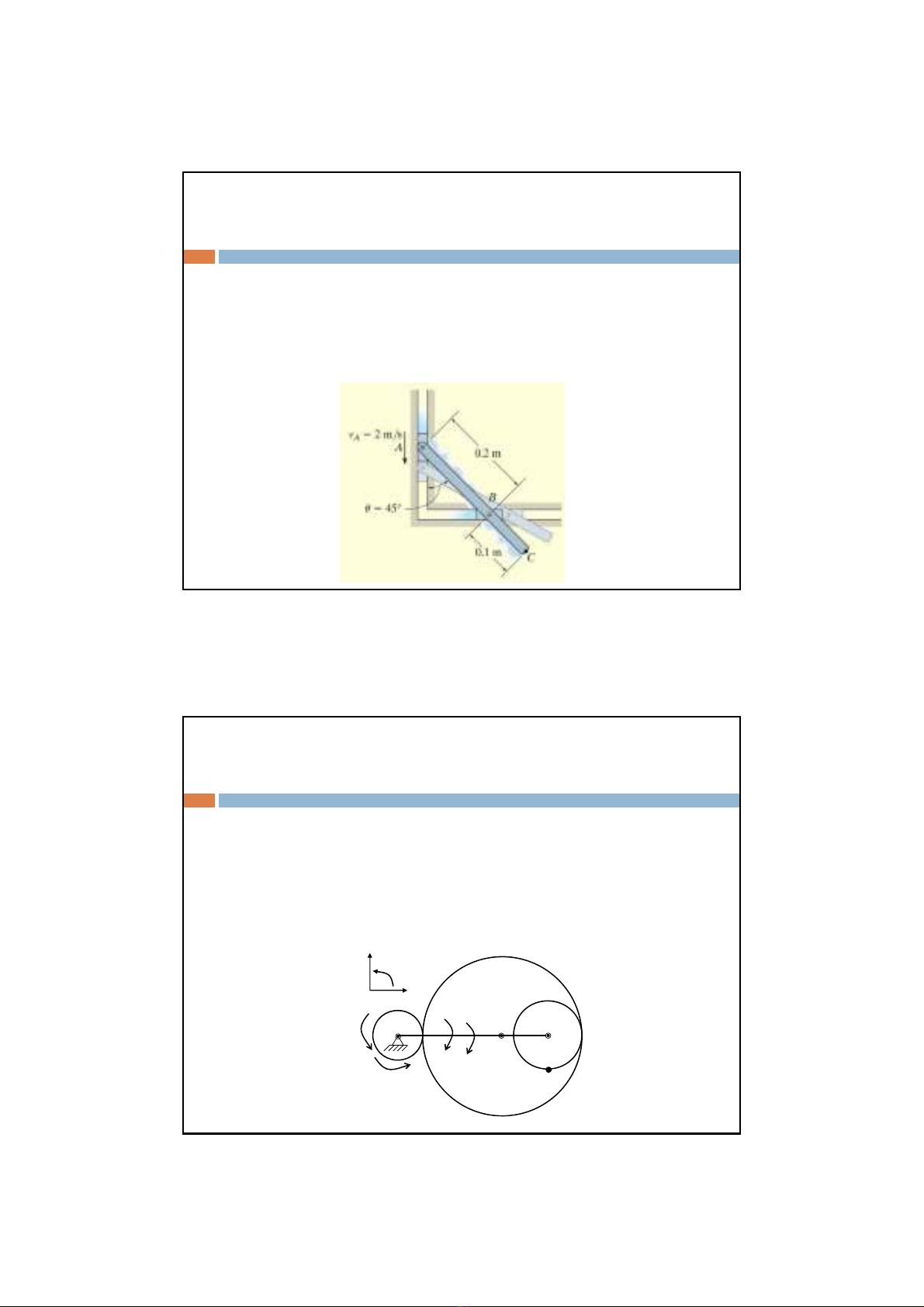
Ví dụ:Cho cơcấuABnhưhình vẽ, A di chuyểnvớivậntốc
2m/s và gia tốc3m/s
2
1) Tính vậntốcvàgiatốcđiểmB
2) Tìm quỹđạocủađiểm C khi A di chuyểntừđộcao cao
nhấtđếnđiểmthấpnhất.
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
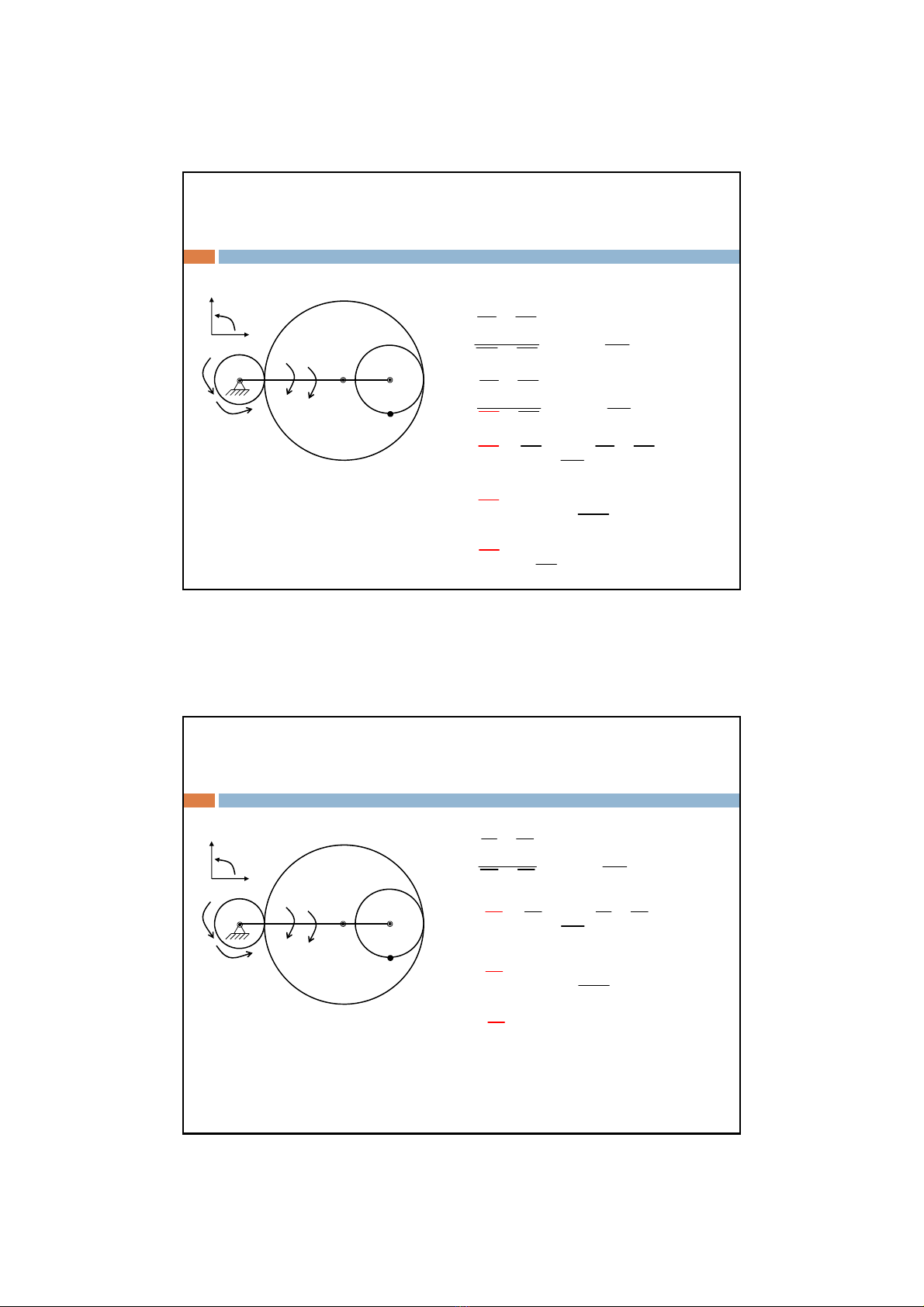
Ví dụ:Cho cơcấu tay quay O1AB quay quanh O1. Ba bánh
răng ănkhớprăng nhưhình vẽ, các bán kính tương ứng R1,
R2,R
3biếtR
1=0,2 m, R2=0,6m, R3=0,3m, 1=1,5 rad/s, 1=0,5
rad/s2,c=2 rad/s, c=1 rad/s2.
1) Tính vậntốc góc và gia tốc góc của bánh răng thứba.
2) Tính vậntốcvàgiatốcđiểmM.
O1AB
1
(I)
(II)
(III)
+x
y
c
1
c
M
Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011
Giảng viên Nguyễn Duy Khương 2
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
O1AB
1
(I)
(II)
(III)
+x
y
c
1
c
M
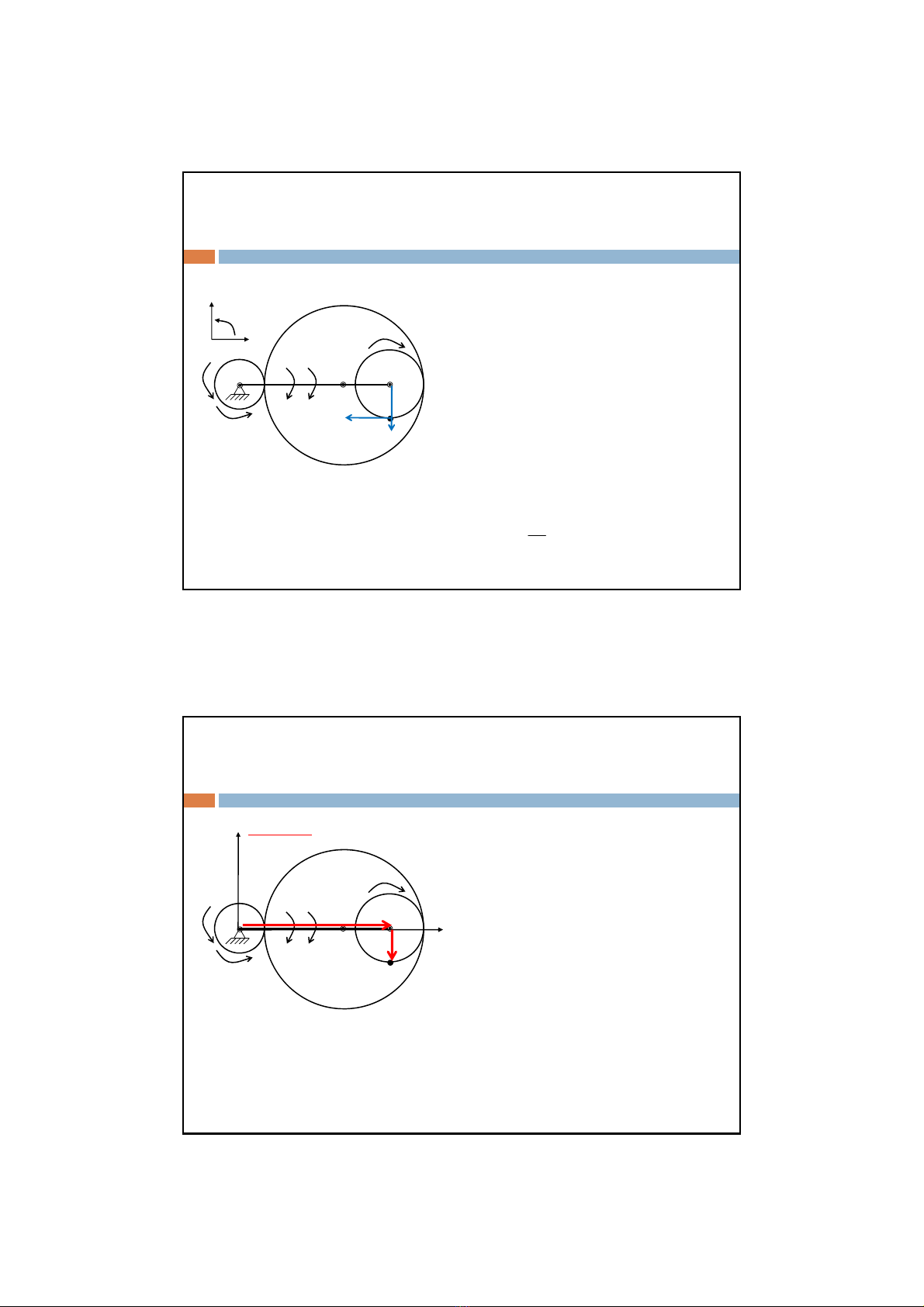
1) Tính vậntốc góc và gia tốc góc của bánh răng thứba
Theo công thức villit ta có:
1
1
(1)
i
cn
nc
R
R



1
13
1
3
(1)
c
c
R
R



1
3
31cc
R
R


 

3
0, 2
21,52
0, 3

3
13 (/)
3rad s

CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
O1AB
1
(I)
(II)
(III)
+x
y
c
1
c
M
Theo công thức villit ta có:
1
1
(1)
i
cn
nc
R
R




1
3
31cc
R
R



3
0, 2
(1) 0,5 (1)
0,3

2
32( / )rad s

Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011
Giảng viên Nguyễn Duy Khương 3
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
O1AB
1
(I)
(II)
(III)
+x
y
c
1
c
M
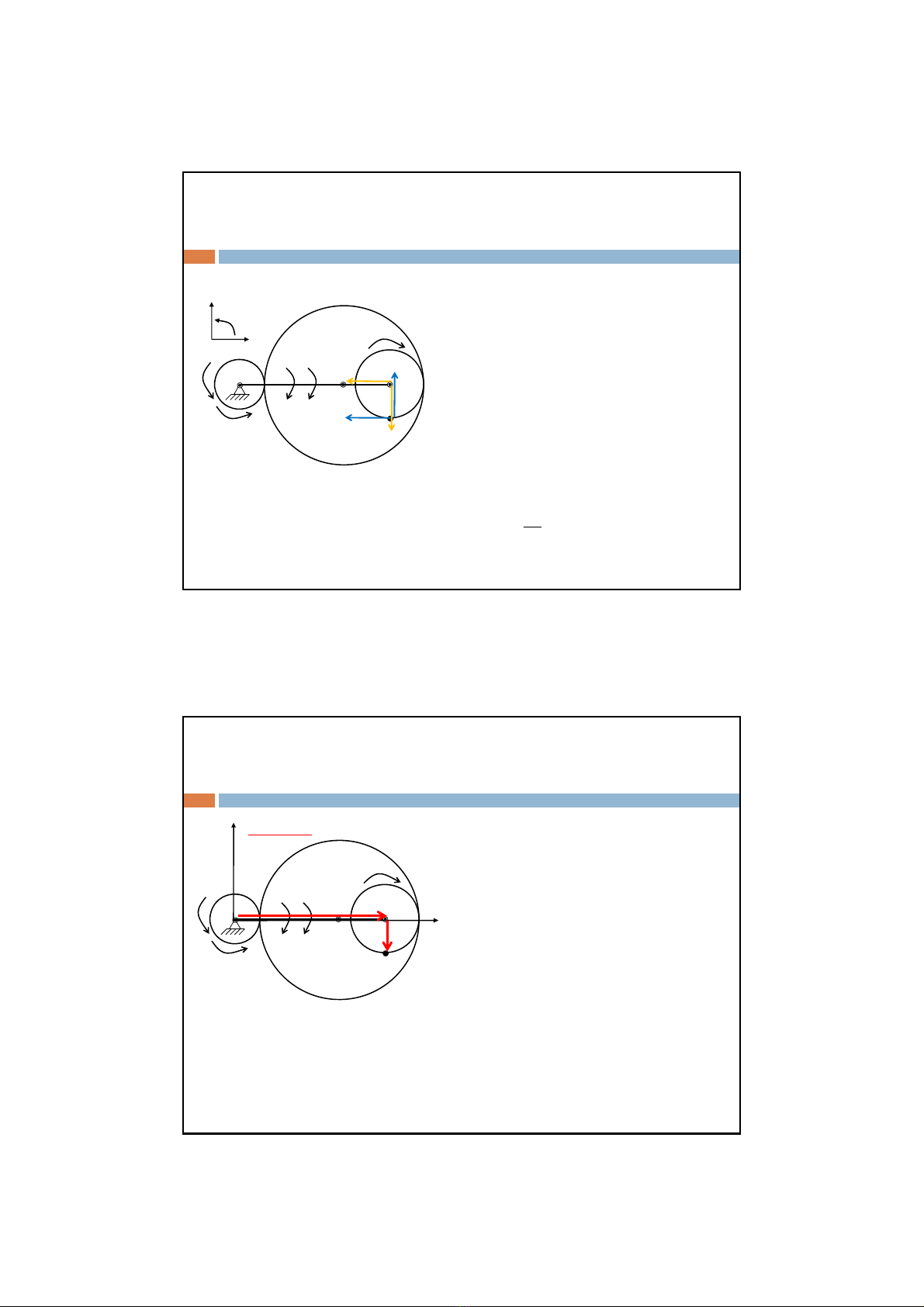
*Bài toán vậntốc
/
BMB
VVV
  
2) Tính vậntốcvàgiatốcđiểmM
Ta chọnBlàmcựctacócôngthức
quan hệsau
3
3
B
V
/
M
B
V
 Do B quay quanh O1nên
1123
.(2)
Bc c
VOBjRRRj
 

Do M có chuyểnđộng quay quanh B
nên
/33MB
VRi


123 33
(2 )
Mc
VRRRjRi

 13
0, 3 (0, 2 2.0, 6 0, 3)2
3ij
1, 3 2, 2ij

CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
O1
A
B
1
(I)
(II)
(III)
x
y
c
1
c
M
Cách 2: Ta c ó th ểtính vậntốcbằng công thứcvector
3
3
123 33
0; 2 ; 0 ; 0; 0
Mc
VRRRR



1, 3 2, 2ij
/
BMB
VVV
  
3MB
VV BM

   
13cOB BM


  
Với
1123 123
2 2 ;0;0OB R R R i R R R 

3
0; ; 0BM R

0; 0;
cc


33
0; 0;



33 1 2 3
;2;0
c
RRRR


BM

1
OB

Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011
Giảng viên Nguyễn Duy Khương 4
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
O1
A
B
1
(I)
(II)
(III)
+x
y
c
1
c
M
*Bài toán gia tốc
/
M
BMB
WWW
  
2) Tính vậntốcvàgiatốcđiểmM
3
3
B
W

/
M
B
W

Do B quay quanh O1nên
n
BBB
WWW



Do M có chuyểnđộng tương đối
quay quanh B nên
22
123 33 33123
22
Mc c
W R RR R iR R RR j

 

54,5ij

2
11cc
OB i OB j

n
B
W

///
n
M
BMBMB
WWW

 

/
n
M
B
W

2
33 3 3
R
iR j





2
213
0, 2 2.0, 6 0, 3 2 0, 3.2 0, 3 0, 2 2.0, 6 0, 3 1
3
i
j








CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
O1
A
B
1
(I)
(II)
(III)
c
1
c
M
/
M
BMB
WWW
  
3
3
Cách 2: Ta c ó th ểtính vậntốcbằng công thứcvector
2
33B
WBMBM


 
2
11
2
33
cc
OB OB
BM BM




 

Với
0; 0;
cc

1123
2;0;0OB R R R

33
0, 0,
3
0; ; 0BM R




2
123 123
2
33 3 3
0; 2 ; 0 2 ; 0; 0
;0;0 0; ;0
Mc c
WRRRRRR
RR





22
1233333 123
;220;
cc
RRR RR RRR


x
y
BM

1
OB

Bài giảng Cơ Học Lý Thuyết - Tuần 6 4/8/2011
Giảng viên Nguyễn Duy Khương 5
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
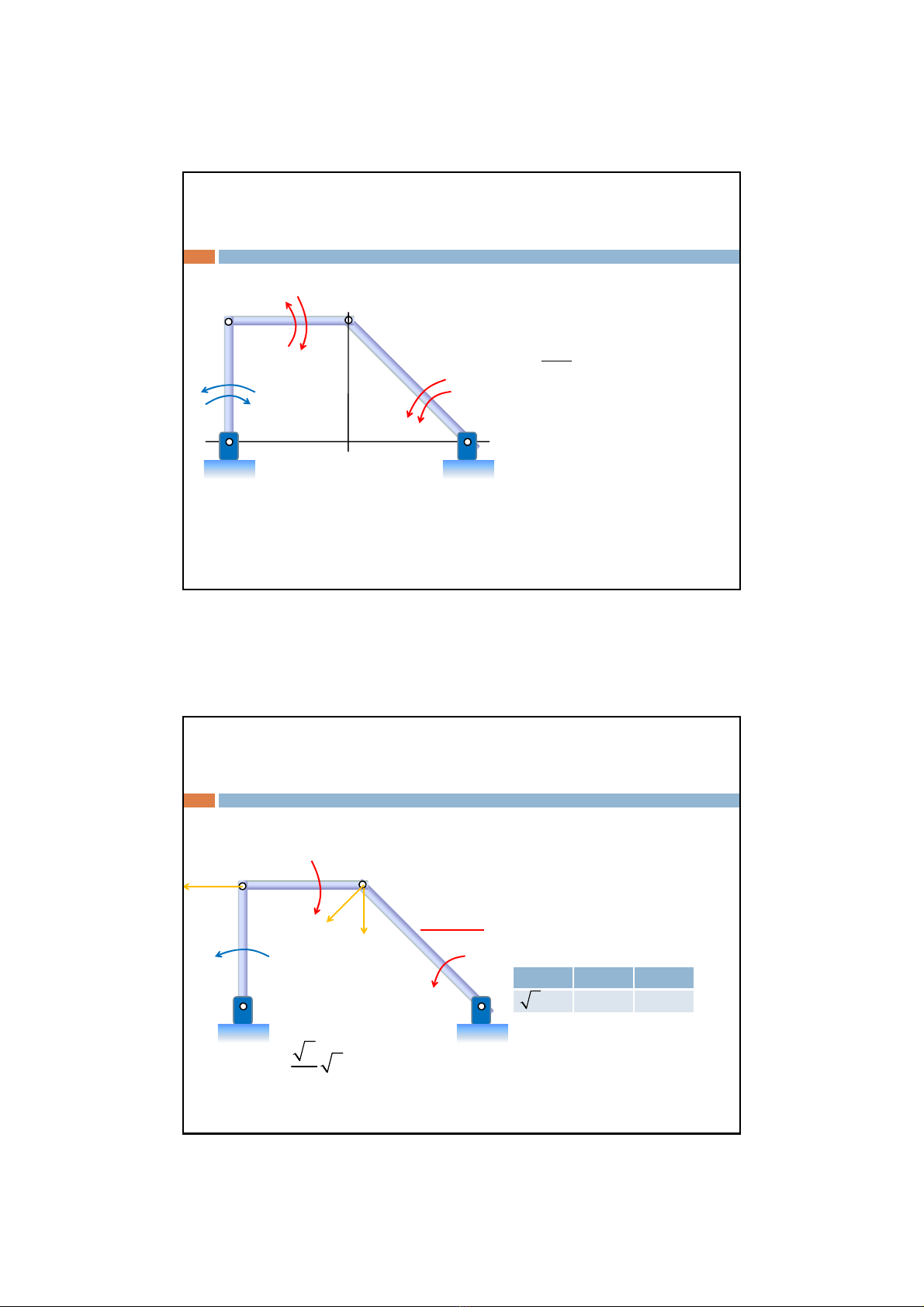
Ví dụ:Chomôhìnhnhưhình vẽ.Biết AB=BC=R
Tính vậntốc góc và gia tốc góc
của thanh BC, CD.
45o
A
B
C
D
R
R
R
1
1
2
2
*Phân tích chuyểnđộng
Giải
+Điểm B quay tròn quanh A
+Điểm C quay tròn quanh D
CHƯƠNG 9 Chuyểnđộng song phẳng củavậtrắn
1. Khảo sát vật chuyển động song phẳng
*Giải bài toán vậntốc
A
B
C
D
1
2
C
V
B
V+Tính vậntốcV
B
B
VR
+Tính vậntốcV
C(Có 3 cách tính VC)
Cách 1: Dùng công thức quan hệvậntốc
/CB
V
1
220
2RR

|_ CD |_ AB |_ BC
1
2
R
R
2
R
Chiếu (*) lên trục x, y
Ox:
/CBCB
VVV
 
(*)
1

Oy: 12
0RR
 2
