CHƯƠNG II
TS. ĐẶNG HOÀI TRUNG
BM VẬT LÝ ĐỊA CẦU, KHOA VL – VLKT, TRƯỜNG ĐH KHTN – VNU-HCM
Email: dhtrung@hcmus.edu.vn
1. TÍCH PHÂN CHUYỂN ĐỘNG – ĐỊNH LUẬT BẢO TOÀN1. TÍCH PHÂN CHUYỂN ĐỘNG – ĐỊNH LUẬT BẢO TOÀN
-Tích phân chuyển động:là các hàm theo tọa độ và
vận tốc suy rộng, luôn giữ nguyên giá trị không đổi và
chỉ phụ thuộc vào điều kiện ban đầu.
-Đnh lý Noether: vi bt kỳ một vi phân đối xng
nào, tác dụng ca một hệ vật lý tương ng vi một định
luật bo toàn
-Yêu cầu: chng minh mỗi bt biến ca hàm Lagrange
đối vi phép biến đổi đối xng ca không gian hoặc
thời gian đều dẫn đến một tích phân chuyển động –
định luật bảo toàn.
Amalie Emmy Noether
(23/3/1882 –14/4/1935)
Nhà toán học người Đức
nổi tiếng vì những đóng
góp nền tảng và đột phá
trong lĩnh vực đại số trừu
tượng và vật lý lý thuyết
2. ĐỊNH LUẬT BẢO TOÀN NĂNG LƯỢNG2. ĐỊNH LUẬT BẢO TOÀN NĂNG LƯỢNG
-Xét tính đồng nhất của thời gian –hàm Lagrange sẽ không phụ thuộc hiển
vào thời gian t.
𝑑𝐿
𝑑𝑡 = ෍
𝑖
𝜕𝐿
𝜕𝑞𝑖
𝜕𝑞𝑖
𝜕𝑡 +෍
𝑖
𝜕𝐿
𝜕 ሶ𝑞𝑖
𝜕 ሶ𝑞𝑖
𝜕𝑡 +𝜕𝐿
𝜕𝑡 = ෍
𝑖
𝜕𝐿
𝜕𝑞𝑖ሶ𝑞𝑖+෍
𝑖
𝜕𝐿
𝜕 ሶ𝑞𝑖ሷ𝑞𝑖= ෍
𝑖
𝑑
𝑑𝑡 𝜕𝐿
𝜕 ሶ𝑞𝑖ሶ𝑞𝑖
𝑑
𝑑𝑡 ෍
𝑖
𝜕𝐿
𝜕 ሶ𝑞𝑖ሶ𝑞𝑖−𝐿 = 0
Đặt là: E
(2.1)
-Đnh lý Euler về các hàm thuần nhất: nếu f (x1, x2, …, xk) là hàm thuần nht
bậc n thì:
𝑥1𝜕𝑓
𝜕𝑥1+⋯+𝑥𝑘𝜕𝑓
𝜕𝑥𝑘=𝑛𝑓
- T là hàm thuần nht bậc 2:
෍
𝑖ሶ𝑞𝑖𝜕𝐿
𝜕 ሶ𝑞𝑖= ෍
𝑖ሶ𝑞𝑖𝜕𝑇
𝜕 ሶ𝑞𝑖= 2𝑇
-Vậy: E là cơ năng ca hệ
ሻ
𝑬 = 𝑻 𝒒, ሶ
𝒒 +𝑼(𝒒 (2.2)
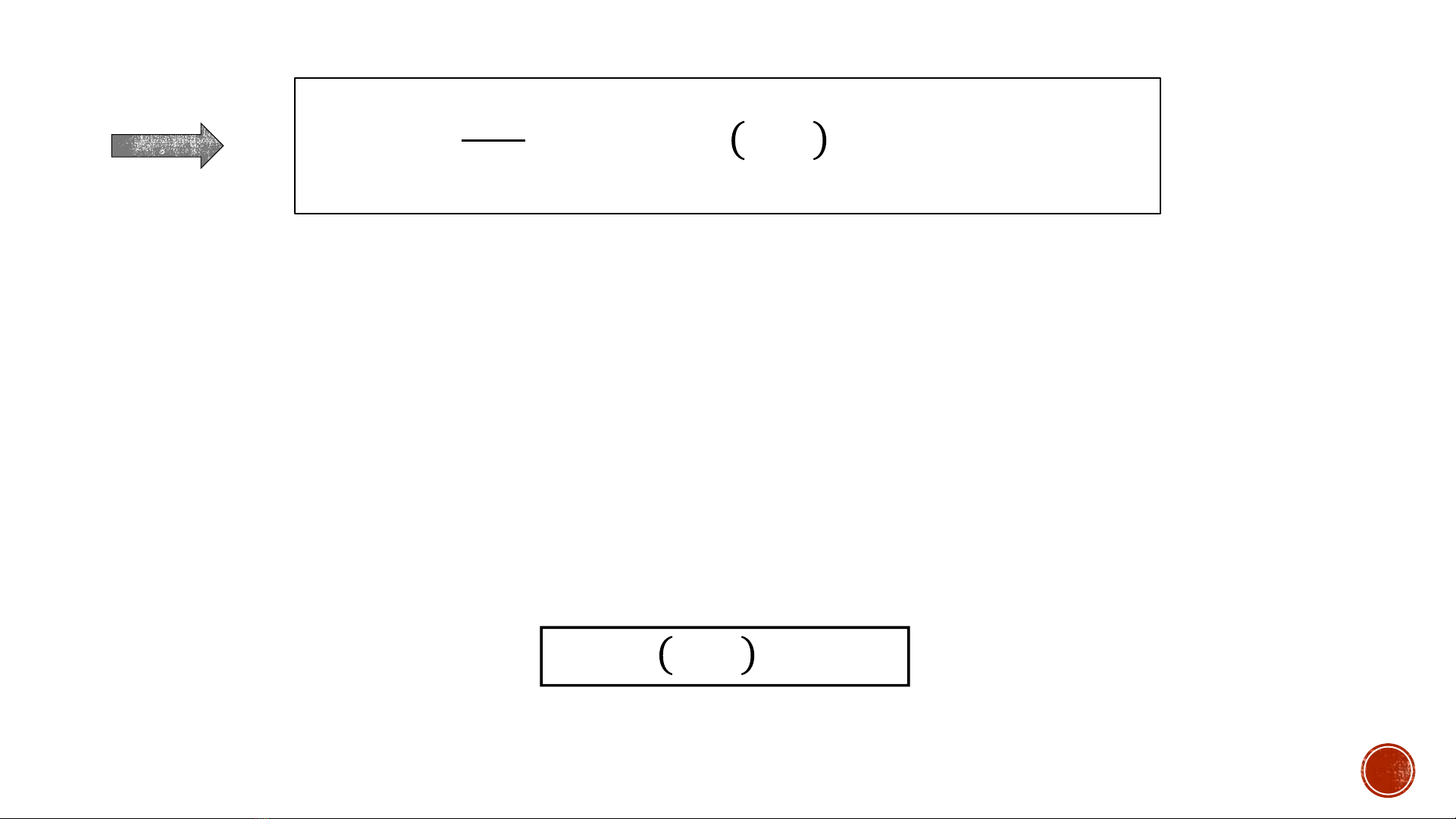
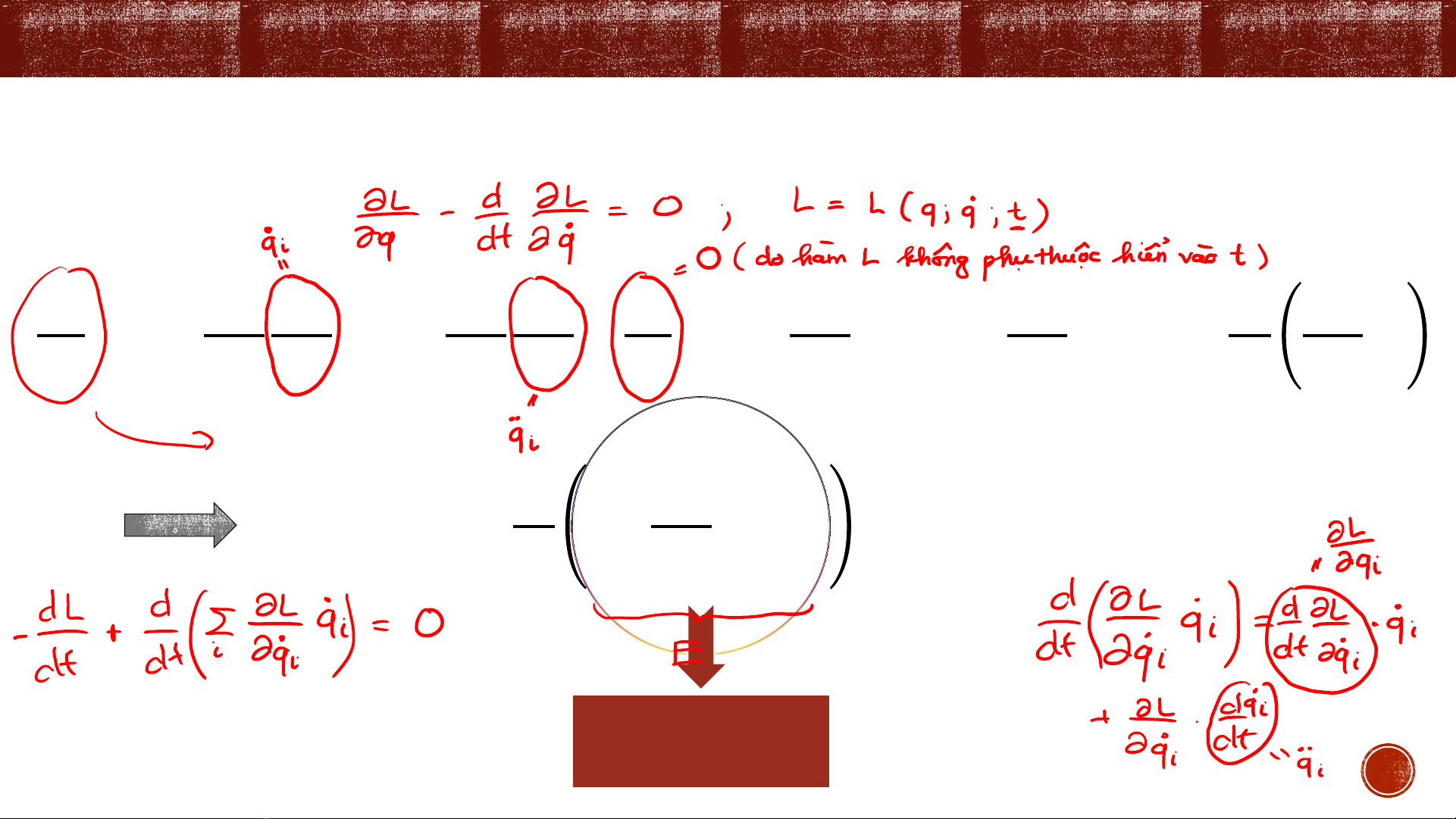
𝑬 = ෍
𝒊
𝜕𝑳
𝜕ሶ
𝒒𝒊ሶ
𝒒𝒊−𝑳 = ሻ
𝑻𝒒, ሶ
𝒒 +𝑼(𝒒 = 𝒄𝒐𝒏𝒔𝑡
(2.1 và 2.2)
-Đnh luật bảo toàn cơ năng: trong cơ hệ kín năng lượng luôn giữ nguyên
không đổi trong suốt quá trình chuyển động.
- Năng lượng có tính cộng được.
-Các hệ cơ học có năng lượng được bo toàn gọi là các hệ bo th.
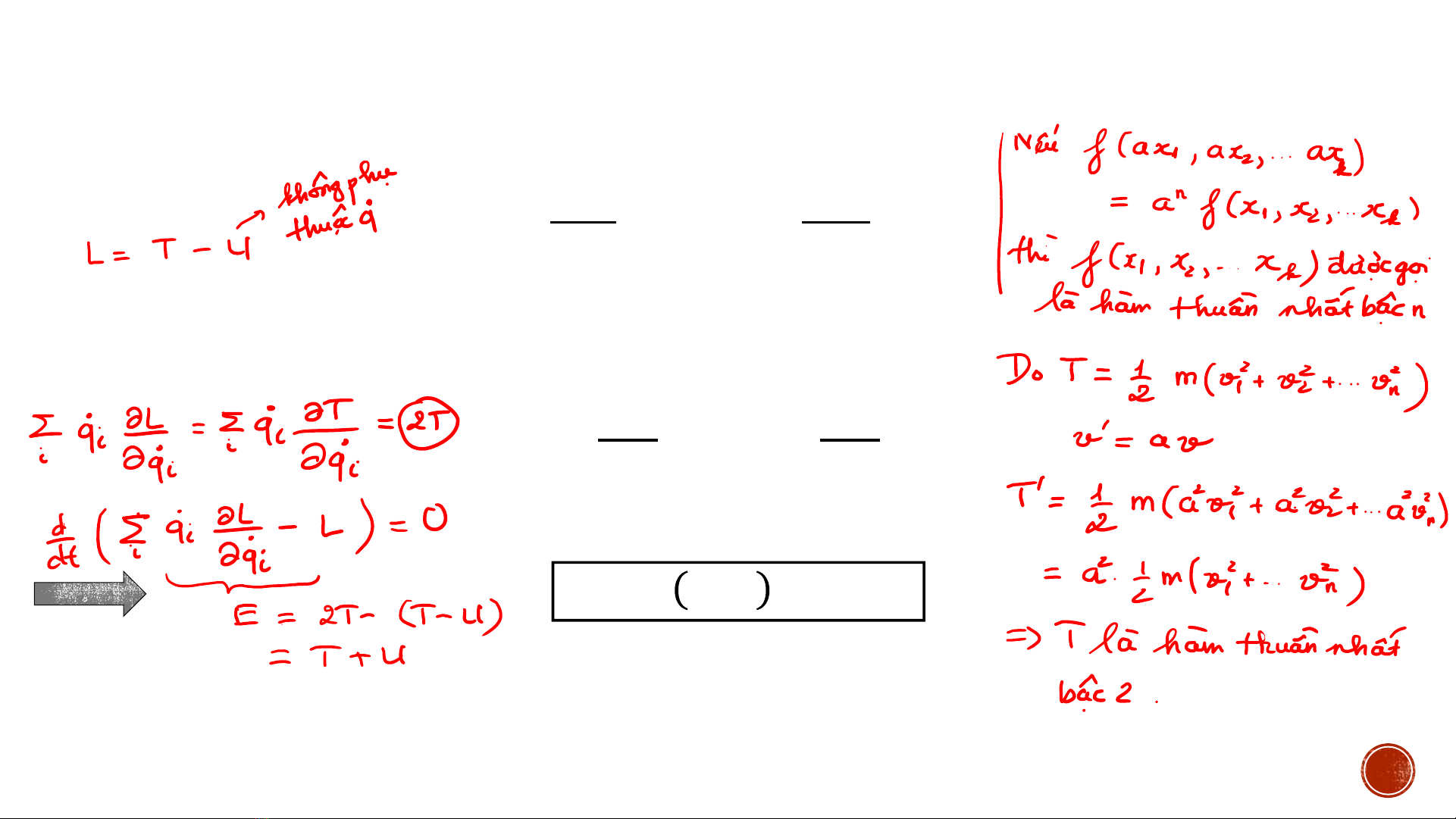
- Hàm Lagrange cho cơ hệ kín (hoặc nằm trong trường ngoài không đổi):
ሻ
𝑳 = 𝑻 𝒒, ሶ
𝒒 −𝑼(𝒒