CÔNG NGHỆ TẠO HÌNH DỤNG CỤ
Thuyết trình: PGS.TS. Bùi Ngọc Tuyên
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN CƠ KHÍ
Bộ môn Gia công vât liệu và dụng cụ công nghiệp
HÀ NỘI 2019
CÔNG
NGHỆ TẠO
HÌNH
DỤNG CỤ
1
2
3
4
Bài mở đầu: Hình học bề mặt
Chương 1: Động học tao hình & động học gia công
Chương 3: Các điều kiện tao hình bề mặt
CÔNG NGHỆ TẠO HÌNH DỤNG CỤ
5
Chương 2: Bề mặt khởi thủy & các phương pháp xác định bề mặt khởi
thủy
Chương 4: Đặc điểm công nghệ chế tạo dụng cụ & các giai đoạn chế
tạo dụng cụ
6 Chương 5: Các nguyên công tạo phôi dụng cụ
2
7 Chương 6: Các nguyên công tạo hình dụng cụ trước nhiệt luyên
8 Chương 7: Các nguyên công tạo hình dụng cụ sau nhiệt luyên
Bài mở đầu: Hình học bề mặt
I. Giới thiệu
Bề mặt cấu thành lên các vật thể, chi tiết máy
Phương trình bề mặt dạng không tham số :
Phương trình bề mặt dạng tham số
[x y z] [x y f(x,y)]
T T
P
min max min max
( , ) [x y z] [x(u,v) y(u,v) z(u,v)]
;
T T
P u v
u u u v v v
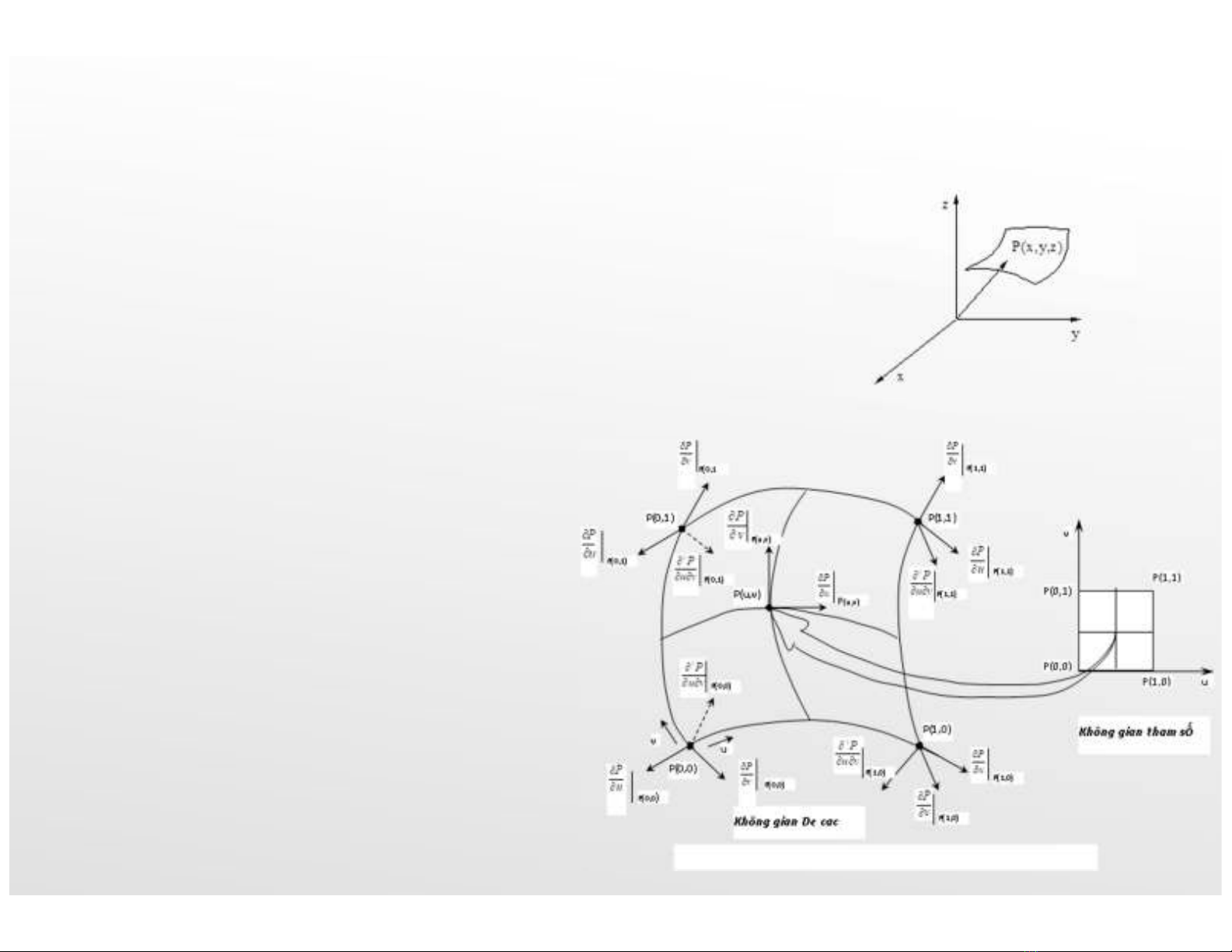
Mỗi mảnh bề mặt cấu trúc 4 cạnh có
một tập hợp các điều kiện biên gồm:
16 vecto và 4 đường cong biên. 16
vecto là: 4 vecto ở vị trí 4 góc P(0,0);
P(1,0); P(1,1) và P(0,1); 8 vecto tiếp
tuyến ở 4 góc (mỗi góc có 2 vecto tiếp
tuyến ứng với 2 đường cong biên u, v
qua điểm góc), 4 vecto xoắn tại 4 điểm
góc 4 đường cong biên là u=0, u=1,
v=0, v=1.
Bề mặt cơ bản
1) Mặt phẳng
2) Mặt kẻ
3) Mặt tròn xoay
4) Mặt trụ
5) Măt xoắn vít
Bề mặt từ các đường cong tổng hợp
Hình thành trên cơ sở các
đường cong tổng hợp
Thừa kế các đặc tính điều
khiển từ đường cong
Hermite
Bezier
B-spline
NURBS.
Bài mở đầu: Hình học bề mặt
Các đặc trưng hình học cơ bản của bề mặt:
Véc tơ tiếp tuyến
→ Vecto tiếp tuyến tại 1 điểm P(u,v) trên bề mặt tham số nhận được bằng cách giữ 1
tham số không đổi và lấy đạo hàm theo tham số kia.
Vecto pháp tuyến
→ Vec tơ pháp tuyến tại 1 điểm bằng tích có hướng của hai vec tơ tiếp tuyến tại điểm đó:
Véc tơ xoắn
→ Vecto xoắn tại một điểm trên bề mặt dùng để đo độ xoắn của bề mặt tại điểm đó. Đó là
tốc độ thay đổi của vecto tiếp tuyến Pu đối với v hay của vecto tiếp tuyến Pv đối với u hay
chính là vecto đạo hàm hỗn hợp.
Độ cong.
→ Độ cong của bề mặt tại 1 điểm P(u,v) được định nghĩa là độ cong của đường cong tiết
diện pháp tuyến nằm trên bề mặt và đi qua điểm này.
- Đô cong chính k1,P; k2,P
- Độ cong trung bình: H=
- Độ cong Gaussian : K = k1, P . k2, P
Bán kính cong
→ Bán kính cong của bề mặt trong tiết diện pháp tuyến bằng nghịch đảo độ cong của
đường cong tiết diện pháp tuyến: r =1/ k .
Bài mở đầu: Hình học bề mặt
1, 1,
2
P P
)v,u(P
v
)v,u(Pv
)v,u(P
u
)v,u(P
u
)v,u(P
v
u
)v,u(P
2
uv
( , ) x x
u v
P P
N u v P P
u v