Bài giảng điều khiển quá trình 8

Chia sẻ: Cindy Cindy | Ngày: | Loại File: PDF | Số trang:11

Thêm vào BST

Báo xấu

113
lượt xem 23
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Đối với hầu hết các hệ thống gia nhiệt thì đặc tính ở trạng thái xác lập được quan tâm là chủ yếu. Xét lại phương trình truyền nhiệt của thiết bị gia nhiệt trạng thái xác lập:

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng điều khiển quá trình 8

Đối với hầu hết các hệ thống gia nhiệt thì đ ặc tính ở trạng thái xác lập được quan tâm là chủ yếu. Xét lại phương trình truyền nhiệt của thiết bị gia nhiệt trạng thái xác lập :  H C pH (TH 1  TH 2 )   C C pC (TC 2  TC 1 ) Ta suy ra  H C pH TC 2  TC1  (TH 1  TH 2 ) (3.102 )  C C pC Có thể thấy quan hệ phi tuyến giữa biến điều khiển trực tiếp c và biến cần điều khiển TC2, bởi ngay cả khi các biến nhiễu (H, TC1, TH1) và các hệ số nhiệt dung riêng (CpH, CpC) được coi như không thay đ ổi thì TH2 cũng đ ã phụ thuộc vào H. Đặt công suất truyền nhiệt q là biến trung gian: q   H C pH (TH 1  TH 2 ) (3.103 ) ta có thể viết: q TC 2   TC1 (3.104 )  C C pC nhìn vào phương trình (3.104), ta có thể nhận ra ngay biến điều khiển cần chọn cho tuyến tính hoá l à u = q/C: 1 TC 2  u  TC1 (3.105 ) C pC mô hình nhận đ ược sau khi biến đổi gồm hai phương trình tuyến tính (3.103) và (3.105) và một phương trình phi tuyến u = q /C. Hiểu theo một cách khác, ta sử dụng phép biến đổi để tách một mô hình phi tuyến thành hai mô hình tuyến tính đ ơn giản hơn.. Thực tế sách lược điều khiển được áp dụng cho các thiết bị gia nhiệt dầu nóng chính là d ựa trên mô hình dẫn suất này. 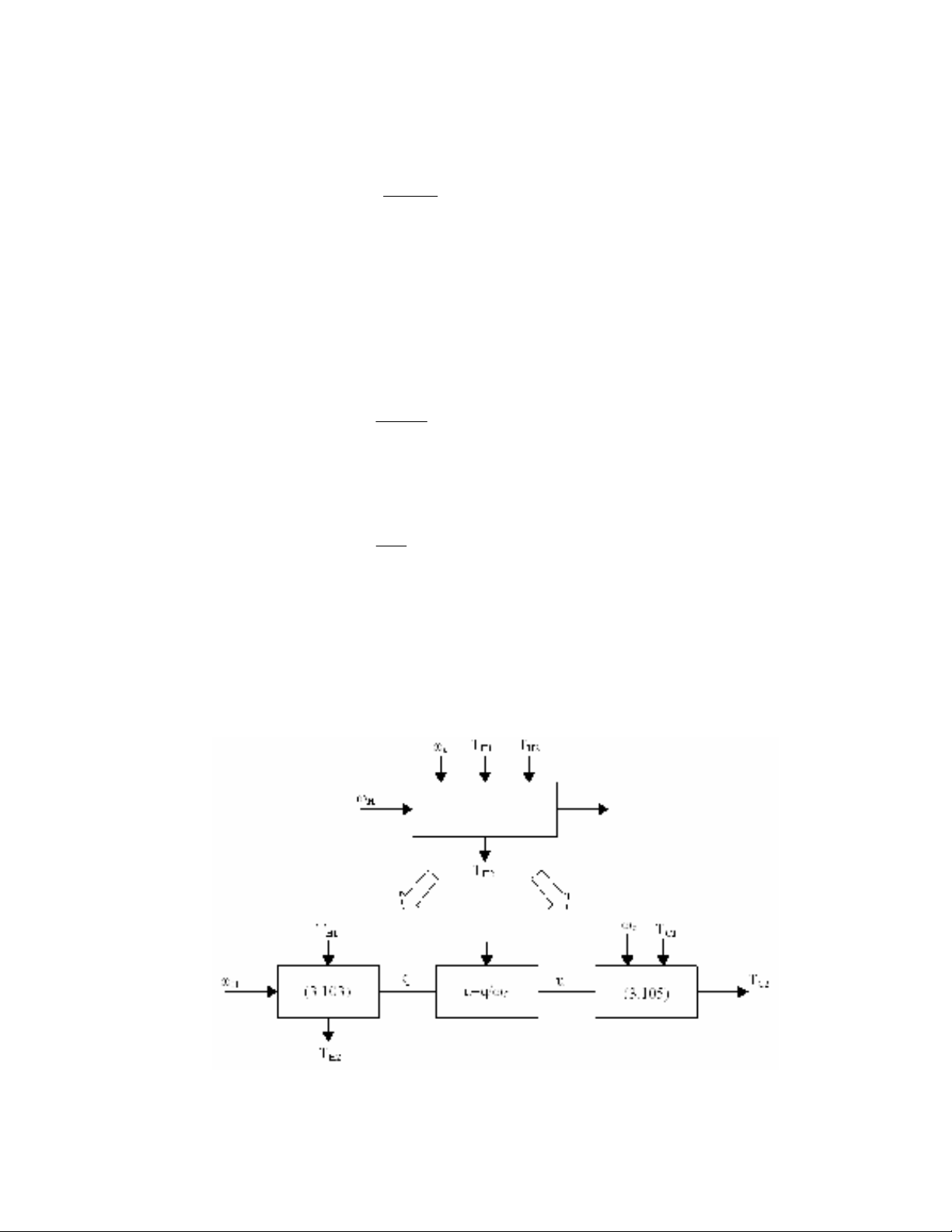Hiệu quả cách làm này được minh hoạ trên hình 3.17. Hình 3.17. Tuyến tính hoá mô hình thiết bị gia nhiệt qua phép biến đổi. http://www.ebook.edu.vn 75
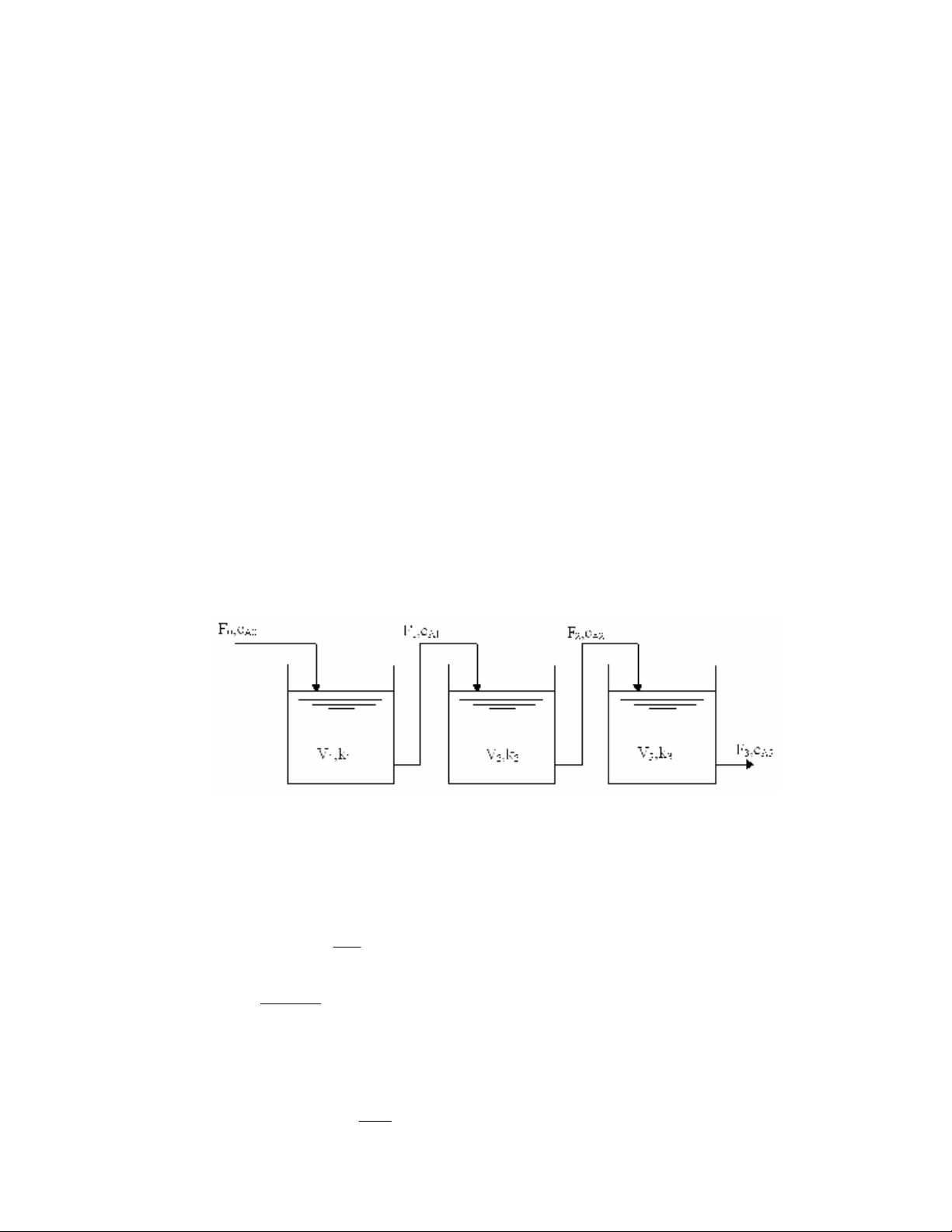
3.6. Một số ví dụ quá trình tiêu biểu 3.6.1. Chuỗi ba thiết bị phản ứng liên tục đẳng nhiệt * Phân tích bài toán Thiết bị phản ứng đẳng nhiệt bây giờ được mở rộng thành chu ỗi gồm ba thiết bị nối tiếp , như minh hoạ trên hình 3.25. Sản phẩm B đ ược tạo thành qua phản ứng nguyên liệu A trong các thiết bị khuấy trộn lý tưởng. Nhiệt độ trong các thiết bị khuấy trộn có thể khác nhau , tuy nhiên ta coi không thay đ ổi do phản ứng là đ ẳng nghiệt. Ta giả thiết khối lượng riêng của các dung dịch trong các thiết bị không khác nhau đáng kể. Tốc độ phản ứng riêng của mỗi thiết bị (k1, k2, k3) phụ thuộc nhiệt độ và nồng độ , vì thế khác nhau. Lưu ý rằng ở đây ta không quan tâm trực tiếp đến nồng độ của B trong các thiết bị bởi đại lượng này được dẫn suất từ nồng độ của A qua phương trình cân b ằng vật chất to àn phần và phương trình vật chất viết cho cấu trúc A. Ta đặt ra mục đích sử dụng mô hình ở đ ây là phục vụ thiết kế sách lược cũng như thu ật toán điều khiển và mô phỏng kiểm chứng. Cũng có thể dễ d àng nhận thấy có 6 biến ra là V1, V2, V3, cA1, cA2 và cA3. Các biến vào trước hết là các lưu lượng F0, F1, F2 và F3, cũng như nồng độ cA0 của dòng nguyên liệu. Tuỳ theo yêu cầu của bài toán điều khiển, lưu lượng vào F0 (cũng như lưu lượng ra F3) có thể được coi là biến điều khiển hoặc nhiễu, và lưu lượng F3 cũng có thể đồng thời đóng vai trò vừa là biến ra vừa là biến vào. Nồng độ cA0 của dòng nguyên liệu chắc chắn đ ược coi là nhiễu. Khối lượng riêng, tốc độ phản ứng riêng và nhiệt độ tại các b ình được coi là tham số quá trình tuy nhiên sự thay đổi của chúng có thể được xếp chung vào nhiễu quá trình ho ặc sai lệch mô hình. Hình 3.25. Chuỗi thiết bị phản ứng liên tục đẳng nhiệt. * Xây dụng các phương trình mô hình Giả thiết các phản ứng có bậc n. Với mỗi thiết bị ta có thể viết ngay các phương trình cân bằng vật chất. Ví dụ cho thiết bị gia nhiệt thứ nhất ta có: dV1 (3.106 )  F0  F1 dt d (V1c A1 )  F0 c A0  F1c A1  V1k1 (c A1 ) n (3.107 ) dt Khai triển đạo hàm vế trái của phương trình thứ hai và sau đó thay thế phương trình thứ nhất vào , ta nhận được dc A1  F0 c A0  F1c A1  V1 k1 (c A1 ) n c A1 ( F0  F1 )  V1 dt http://www.ebook.edu.vn 76
Hay rút gọn hơn F F dc A1   0 c A1  k1 (c A1 ) n  0 c A0 (3.108 ) dt V1 V1 Tương tự (3.106) và (3.108), ta có các phương trình mô hình tương ứng với hai thiết bị còn lại: dV2 (3.109 )  F1  F2 dt dV3 (3.110 )  F3  F2 dt dc A2 F F   1 c A2  k 21 (c A2 ) n  1 c A1 (3.111 ) dt V2 V2 dc A3 F F   2 c A3  k 3 (c A3 ) n  2 c A 2 (3.112 ) dt V3 V3 Mô hình nhận được chứa tổng cộng 6 phương trình vi phân phi tuyến thể hiện quan hệ giữa 11 biến: (3.106), (3.3.108) – (3.112). Tham số mô hình giờ đây bao gồm các tốc độ phản ứng riêng (k1, k2, k3) và bậc của phản ứng n. * Phân tích bậc tự do Mô hình cho hệ thống dãy ba thiết bị phản ứng đẳng nhiệt có 5 bậc tự do, trong khi có 6 biến ra. Điều đó có nghĩa là ta chỉ có thể thiết kế tối đa 5 vòng điều khiển. Tuy nhiên số biến điều khiển nhiều lắm là 4, vì thế chỉ có thể điều khiển độc lập tối đa 4 biến ra. Nếu mức chất lỏng trong các thiết bị đ ược chọn điều khiển thì chỉ còn một trong ba biến nồng độ có thể chọn là biến được điều khiển. Tuỳ theo yêu cầu của bài toán điều khiển, nếu một trong hai biến lưu lượng (F0, F3) cũng lại đ ược coi là nhiễu thì bài toán điều khiển chất lượng sản phẩm sẽ không đ ược giải quyết. Bây giờ ta xét hệ thống điều khiển mức chất lỏng trong các thiết bị đ ã được giữ cố định bởi ba bộ điều khiển mức. Khi đó cả 4 biến lưu lượng phụ thuộc lẫn nhau theo nguyên lý cân bằng khối lượng, tức là số biến độc lập giảm đi 3. Giải thích theo một cách khác thì việc đưa vào 3 vòng điều khiển mức cũng chính là bổ sung 3 phương trình độc lập. Trong khi đó, 3 b iến chủ đạo cho các giá trị mức cũng đ ược cần thêm vào. Số b ậc tự do của hệ thống không hề thay đổi, nhưng ý nghĩa số bậc tự do đã thay đổi. * Tuyến tính hoá mô hình Để đơn giản hoá trong việc xây dựng mô hình tuyến tính, ở đây ta cũng giả thiết thể tích trong mỗi thiết bị phản ứng đ ã được giữ ổn định bằng một vòng điều khiển mức độc lập. Như vậy cũng có nghĩa là F1 = F2 = F3 = F0 = F. Tiếp theo, giả sử phản ứng là bậc 2, tức n = 2. ở trạng thái xác lập ta có: F F cA1  k 1 ( cA1 ) 2  cA 0 0 V1 V1 F F c A 2  k 2 (c A 2 ) 2  (3.113) 0 c A1 V2 V2 http://www.ebook.edu.vn 77
F F c A 3  k 3 ( c A3 ) 2  0 c A2 V3 V3 giải lần lượt từng phương trình bậc 2 trong (3.113 ) và chỉ lấ y nghiệm dương ta nhận được các giá trị c A1 , c A2 , c A3 tại điểm làm vệc. Đặt các biến chênh lệch  x1   c A1  u  F , d  c A 0 , x   x 2    c A 2  , y  x 3    x3    c A 3    Khai triển Taylor cho các phương trình (3.108), (3.111), và (3.112 ), ta có hệ phương trình vi phân tuyến tính c  c A1 dx1 F F  x1  2k1c A1 x1  A0 (3.114) u d dt V1 V1 V1 c  c A2 dx2 F F x2  2k 2 c A2 x2  A1 (3.115)  u x1 dt V2 V2 V2 c  c A3 dx3 F F x 3  2 k 3 c A3 x 3  A 2 (3.116)  u  x2 dt V3 V3 V3 Hay viết gọn lại dưới dạng mô hình trạng thái 1   c A0  c A1  0 0 F     1 V1 V       c A1  ca 2 u   0  d 1 F 1   (3.117) x 0 x   V  2 V 0 2 2  c  c   1 F  0  A3  A2    3   V3  V3     y  0 0 1x trong đó V1 V2 V3 1  , 2  3  , F  2V1 k1c A1 F  2V2 k 2 c A 2 F  2V3 k 3 c A3 từ mô hình trạng thái tuyến tính (3.108) ta cũng có thể biến đổi sang mô hình ma trận truyền đạt. Tuy nhiên, cách làm này ở đ ây khó cho ta cái nhìn sâu sắc về mặt vật lý. Nếu chỉ cần mô hình hàm truyền đạt thì nên bắt đầu từ phương trình (3.114), (3.115), 3 .116). Ta viết 3 phương trình này gọn lại sau đây: dx1   x1  k u1u  k d 1d dt dx2   x 2  k u 2 u  k d 2 x1 (3.118 ) dt dx3   x1  k u 3u  k d 3 x 2 dt trong đó http://www.ebook.edu.vn 78
c A0  c A1 F , k u1  k d1  F  2V1k1c A1 F  2V1 k1c A1 c A1  c A2 F ku 2  kd 2  , F  2V2 k 2 c A 2 F  2V2 k 2 c A2 c A 2  c A3 F , ku3  kd 3  F  2V3 k 3 c A3 F  2V3 k 3 c A3 Biến đổi Laplace cho cả hai vế của từng phương trình trong (3.118) và đưa về dạng chuẩn ta có: k u1 k u (s )  d1 d (s ) (3.119 ) x1 ( s )   1s  1  1s  1 ku2 k u (s )  d 2 x1 ( s ) (3.120 ) x2 ( s)  2s 1  2s 1 ku3 k u ( s)  d 3 x 2 ( s) (3.121 ) x3 (s )   3s  1  3s  1 Thay thế lần lượt (3.120 ) và (3.119 ) vào (3.121), ta có : k  k u3 k k u ( s )  d 3  u 2 u (s )  d 2 x1 (s )  y( s )  x3 ( s )   s  1  3s 1  3s  1  2 2s 1  k   k u1  ku 2 k d 3 kd 2kd 3 k d1   u3    s  1 ( s  1)( s  1) u ( s)  ( s  1)( s  1)   s  1 u ( s )   s  1 d ( s )     1  3  2 3 2 3 1 k u 3 ( 1 s  1)( 2 s  1)  k u 2 k d 3 ( 1 s  1)  k u1 k d 2 k d 3 k d1 k d 2 k d 3  u (s)  d ( s) ( 1 s  1)( s  1)( 3 s  1) ( s  1)( s  1)( s  1) 2   1 23    G (s) Gd ( s ) (3.122 ) 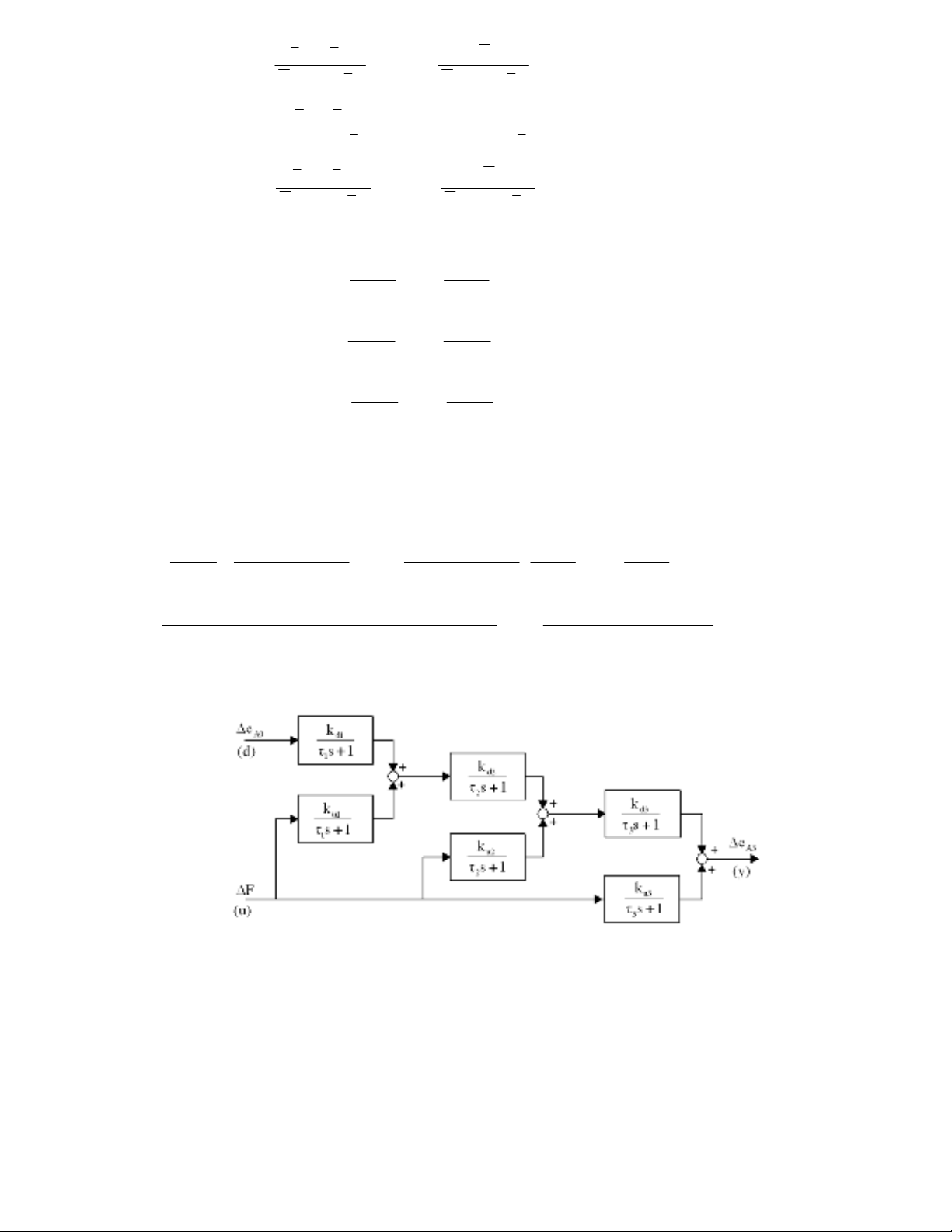Hình 3.26. Sơ đồ khối mô hình chu ỗi 3 b ình phản ứng đẳng nhiệt. Mô hình nhận được bao gồm G(s) và Gd(s), lần lư ợt là hàm truyền từ lưu lượng và từ nồng độ dòng vào tới nồng độ sản phẩm. Có thể thấy, sự mắc nối tiếp các thiết bị phản ứng tạo nên một hệ bậc 3. Đối với những hệ có quá trình tương tác phức tạp, không bao giờ ta cũng có thể tính toán hàm truyền cho cả hệ một cách đơn giản như trên. Thay vì vậy, ta có thể sử dụng công cụ sơ đồ khối để biểu diễn và phân tích hệ thống. Sơ đồ khối cho chuỗi 3 b ình phản ứng biểu diễn trên hình 3.26. http://www.ebook.edu.vn 79
3.6.2. Thiết bị phản ứng thu nhiệt sợi đốt Phân tích bài toán Quá trình phản ứng liên tục đã đ ề cập đựợc mở rộng cho trường hợp phản ứng thu nhiệt, như minh ho ạ trên hình 3.27. Dòng vào là A nguyên chất, sản phẩm tạo ra sau phản ứng A  B là hỗn hợp A và B. Thiết bị phản ứng được trang bị thêm sợi đốt để duy trì nhiệt độ phản ứng tại một giá trị phù hợp. Mục đích xây dựng mô hình là phục vụ phân tích và hiểu rõ tính động học của quá trình tạo cơ sở cho thiết kế sách lược và thuật toán điều khiển. Trước hết ta đưa ra các giả thiết sau: Hình3.27. Thiết bị phản ứng thu nhiệt sợi đốt. Thiết bị khuấy trộn lý tưởng, nghĩa là nhiệt độ và nồng độ tại mọi điểm giống nhau và giống nhiệt - độ và nồng độ ra. Áp su ất và khối lượng riêng của dòng quá trình, trước cũng như sau phản ứng, đ ược coi là không - thay đổi đáng kể. Với giả thiết trên hệ thống bao gồm tổng cộng 8 biến quá trình. Trên cơ sở đó có thể dễ nhận hấy rằng có 5 biến vào (F0, T0, cA0, F, ρ) và 3 biến ra (V, T, cA). Phân tích các mục đích điều khiển kết hợp với sơ đồ công nghệ, ta tiếp tục nhận biết các biến cần điều khiển, các biến điều khiển tiềm năng và các biến nhiễu minh hoạ trên hình 3.28. Xây d ựng các phương trình mô hình Hình 3.28: Các biến quá trình trong phản ứng thu nhiệt sợi đốt http://www.ebook.edu.vn 80
Thiết bị phản ứng là một là một ví dụ mô hình hoá tương đ ối tiêu biểu, bởi vì trong đ ó có áp dụng nhiều quan hệ hoá lý cơ bản. Trước hết ta có thể viết lại phương trình cân bằng vật chất to àn phần: dV  F0  F (3.123 ) dt Quá trình phản ứng đ ược coi là bậc nhất, nên phương trình cân bằng thành phần được viết tương tự (3.15) n F dc A F    k c A  0 c A0 (3.124 ) dt V V  và tốc độ phản ứng riêng k còn phụ thuộc nhiệt độ theo hàm lu ỹ thừa (3.46) k  k 0 e  E / RT (3.125 ) Để xây dựng phương trình cân bằng năng lượng, trước hết ta thấy rằng công suất thu nhiệt do quá trình phản ứng hấp thụ qR tỷ lệ thuận với tốc độ phản ứng: q R  Vkc A (3.126) Hệ số sinh nhiệt  có dấu âm đối với phản ứng toả nhiệt và dấu d ương với phản ứng thu nhiệt. ta có thể đ ưa ra giả thiết là thế năng và động năng không đáng kể so với nội năng. Phương trình cân b ằng năng lượng được viết như sau: d ( Vu )  F0  0 u 0  Fu  (q  q R )  ( FP  F0 P0 ) dt ˆ ˆ  F0  0 (u 0  PV0 )  ( F (u  PV ) (3.127 ) ˆ Đối với chất lỏng, thành phần năng lượng PV không đáng kể so với nội năng u , vì vậy phương trình (3.127 ) có thể viết lại thành: d ( Vh )  F0  0 h0  Fh  q  Vkc A (3.128 ) dt Trong điều kiện áp suất và nồng độ không thay đổi đáng kể, nhiệt dung riêng có thể coi là hằng số. Tiếp tục giả thiết khối lượng riêng của các d òng chảy là hằng số , tức là  = 0 = const. Áp dụng quan hệ (3.26 ), sau khi rút gọn ta có phương trình cân bằng nhiệt biểu diễn trực tiếp các biến nhiệt độ: d (VT ) 1 (q  Vkc A ) (3.129 )  F0T0  FT  C P dt khai triển đạo hàm bên vế trái của phương trình (3.129) dV dT 1 V  F0 T0  FT  (q  Vkc A ) T C p dt dt và thay thế dV/dt từ phương trình cân b ằng vật chất (3.123) : dT 1 (q  Vkc A ) T ( F0  F )  V  ( F0T0  FT )  C p dt Rút gọn hai vế phương trình cân b ằng nhiệt trở thành: http://www.ebook.edu.vn 81
dT F0 1 1 kc A  (T0  T )  q (3.130 ) C p V C p dt V Phân tích bậc tự do Mô hình nhận đ ược gồm 8 biến quá trình (q , V, F0, F, T0, T, c0, c). Ba phương trình mô hình đ ược xây dựng lần lượt là: P hương trình cân bằng vật chất to àn phần (3.123), p hương trình cân bằng thành phần (3.124), và phương trình cân b ằng nhiệt (3.130 ). Số bậc tự do của mô hình là 8 – 3 = 5. Thực ra ta cũng còn một phương trình mô hình quá trình là quan hệ giữa tốc độ phản ứng và nhiệt độ (3.125), nhưng nếu xết cả phương trình đó thì số biến quá trình sẽ tăng thêm 1 (tốc độ phản ứng riêng k), nên hệ số bậc tự do không thay đổi. Đối với bài toán thiết bị phản ứng ta chưa phân tích k ỹ các mục đích điều khiển, nhưng trên cơ sở phân tích bậc tự do ta có thể có những kết luận sơ bộ. Trước hết, số lượng tối đa biến phụ thuộc (tức là số biến đầu ra) có thể điều khiển được cũng chỉ bằng số phương trình, tức là 3. Thứ hai nếu đ ã chọn 3 biến cần điều khiển (Ví dụ V, T và c), thì 5 biến còn lại phải là biến vào thì mô hình mới nhất quán. Trong trường hợp này, ta xét thấy hoàn toàn hợp lý. Tiếp theo, nếu chọn 3 biến cần điều khiển thì chúng ta cũng phải chọn 3 b iến điều khiển từ 5 biến vào. Yêu cầu trên chỉ có thể được thoả mãn nếu ta bổ sung thêm một van điều khiển trên dòng lưu lượng để thay đổi lưu lượng F0. Trường hợp F0 lại do quá trình trước quyết định thì số lượng biến tối đa có thể điều khiển được độc lập ở đây chỉ còn lại là 2 (Ví d ụ V và c ho ặc V và T). Thực tế là nồng độ c phụ thuộc vào T, nên ta chỉ có thể gián tiếp điều khiển nồng độ thông qua nhiệt độ. 3.6.3. Thiết bị phản ứng liên tục toả nhiệt Phân tích bài toán Hình 3.29. Thiết bị phẩn ứng liên tục toả nhiệt. Mô hình thiết bị phản ứng liên tục đã được đề cập cần thiết phải mở rộng theo hướng thực tế hơn. Sơ đồ hệ thống được minh hoạ trên hình 3.29. Ở đây lò phản ứng toả nhiệt. Thiết bị lò phản ứng trang bị vỏ làm mát, trong đó nước lạnh đ ưa vào làm mát với nhiệt độ mong muốn. Mục đích xây dựng mô hình là thiết kế sách lược và thuật toán điều khiển, vì vậy cần làm rõ biến cần điều khiển, b iến điều khiển và http://www.ebook.edu.vn 82
nhiễu. Các khả năng can thiệp đ ược thể hiện trên sơ đồ công nghệ. Tương tự như các hệ thống phản ứng khác, yêu cầu đặt ra cho b ài toán ở đ ây là ổ n định vận hành, nâng cao chất lượng sản phẩm, an toàn và tiết kiệm năng lượng. Vì nồng độ phụ thuộc vào nhiệt độ nên ổn định nhiệt độ cũng là một giải pháp để nâng cao chất lượng sản phẩm. Bên cạnh các giả thiết như trong ví d ụ thu nhiệt sợi đốt ta cần bổ sung một số giả thiết sau : Phản ứng có bậc n, tức là phản ứng tổng thể phụ thuộc vào bậc n của nồng độ. - Nhiệt độ nước làm mát đ ều như nhiệt độ đo tại điểm ra. - Vỏ làm mát được lấp đầy nước lạnh tức là thể tích nước lạnh (vj) cũng như bề mặt trao đổi nhiệt - (AH) không đổi. Hình 3.30. các biến quá trình trong thiết bị phản ứng toả nhiệt. Với các giả thiết trên, hệ thống bao gồm 10 biến quá trình. Phân tích trên cơ sở nhân quả ta có thể phân biệt 6 biến vào (F0, T0, cA0, F, Fj, Tj0) và 4 biến ra (V, T, cA, Tj). Phân tích các mục đích điều khiển kết hợp với sơ đồ công nghệ, ta tiếp nhận được các biến cần điều khiển, biến điều khiển và biến nhiễu như minh ho ạ trên hình 3.30. Ngay ở đ ây ta nhận ra 3 biến ra (V, T, cA) không thể điều khiển độc lập, nếu sử dụng hai biến điều khiển. Việc chọn các biến vào được điều khiển chờ sau khi phân tích phương trình mô hình. Chú ý rằng, nhiệt độ nước làm lạnh Tj cũng là một biến ra, nhưng không cần điều khiển. Xây dựng các phương trình mô hình quá trình Tương tự như ví dụ trước, ta viết lại các phương trình cân bằng vật chất cho quá trình phản ứng; dV  F0  F (3.131 ) dt F dc A F     k c A  0 c A 0 (3.132 ) dt V V  k  k 0 e  E / RT (3.133 ) Khác với ví dụ trước ở đây ta phải quan tâm đến phương trình truyền nhiệt, trên cơ sở đó xây dựng phương trình cân bằng nhiệt cho cả thiết bị làm mát bên trong và phần vỏ làm mát. Công su ất truyền http://www.ebook.edu.vn 83
nhiệt giữa quá trình phản ứng tại nhiệt độ trung bình T và dòng nước lạnh tại nhiệt độ trung bình Tj đ ược xác định theo công thức (3.40) : Q  uAH (T  T j ) (3.134 ) Công suất nhiệt sinh ra do phản ứng tỷ lệ với tốc độ phản ứng: QG  Vkc n (3.135 ) A trong đó  có dấu âm. Với giả thiết đã đặt ra, ta dễ dàng xây d ựng phương trình cân bằng năng lượng cho thiết bị phản ứng và vỏ làm mát như sau : d (Vh )   (F0 h 0  Fh )  uA H (T  Tj )  Vkc A (3.136) dt d (Vh j ) j   j (Fj0 h j0  Fjh j )  uA H (T  Tj ) (3.137 ) dt trong đó :  - khối lượng riêng của dòng quá trình (kg/m3), được coi là hằng số 0 – khối lượng riêng của nước làm lạnh (kg/m3), được coi là hằng số h0 – enthanpy của dòng vào quá trình (j/kg) h – enthanpy của dòng ra quá trình (j/kg) h0j – enthanpy của dòng vào của nước làm lạnh (j/kg) hj – enthanpy của dòng ra nước làm lạnh (j/kg) Sử dụng enthanpy và nhiệt độ theo (3.15 ), phương trình cân bằng nhiệt lượng cho thiết bị phản ứng trước hết đ ược biểu diễn như sau: d(VT )  C p (F0 T0  FT)  uA H (T  Tj )  Vkc n C p A dt với CP nhiệt dung riêng của dòng quá trình và được coi là một hằng số. Khai triển đạo hàm hai vế, thay thế đạo hàm dV/dt từ (3.131) và tốc độ phản ứng riêng từ (3.133 ), ta nhận được: dT F0 1 1 k 0 e  E / RT c A n (3.138 )  (T0  T )  uAH (T  T j )  VC P C P dt V Phương trình cân bằng nhiệt lượng cho phần vỏ làm mát cũng được viết lại sử dụng biến nhiệt độ như sau : dT j Fj uAH (3.139 )  (T j 0  T j )  (T  T j )  jV j C Pj dt Vj trong đó CPj là nhiệt dung riêng của nước làm lạnh và được coi là một hằng số. Mô hình nhận được gồm 4 phương trình (3.131 ), (3.132), (3.138) và (3.139) đúng bằng số biến ra. Phân tích bậc tự do Với tổng cộng 10 biến quá trình và 4 phương trình đ ộc lập, số bậc tự do của mô hình là 6, đúng bằng số biến vào. Như vậy, mô hình đ ã đảm bảo tính nhất quán. Tuy nhiên, số biến điều khiển là 2, nên http://www.ebook.edu.vn 84
chỉ hai trong 3 biến ra (V, T, cA) có thể điều khiển độc lập một cách đồng thời. Để đảm bảo vấn đề an toàn, thể tích hoặc mức trong thiết bị phản ứng nhất định phải được khống chế. Để điều khiển hai biến còn lại ta có các phương án sau: 1. Bổ sung van điều khiển trên dòng vào của chất phản ứng nếu cho phép (chất phản ứng được cấp từ một b ình chứa có dung tích đủ lớn) 2. Điều khiển nhiệt T để đảm bảo an toàn, đồng thời thông qua đó gián tiếp điều khiển nồng độ cA. 3. Sử dụng sách lược điều khiển lựa chọn, trong trường hợp bình thường điều khiển nồng độ cA. 4. Sử dụng sách lược điều khiển nối tầng, vòng đ iều khiển trong điều khiển nhiệt độ và vòng điều khiển ngo ài điều khiển nồng độ. Giả thiết nước lạnh trong vỏ làm mát có nhiệt độ đồng nhất thực tế là không hoàn toàn hợp lý. Trong nhiều trường hợp ta có thể đơn giản sử dụng thêm một biến trung gian cho nhiệt độ trung bình trong vỏ làm mát: 1 (3.140 ) T jA  (T j 0  T j ) 2 Khi đó phương trình (3.139 ) được viết lại thành: dT jA Fj uAH (3.141 )  (T j 0  T j )  (T  T jA )  jV j C Pj dt V j C Pj Mô hình nhận đ ược gồm 11 biến quá trình và 5 phương trình, số bậc tự do không hề thay đổi. http://www.ebook.edu.vn 85