zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Kỹ Thuật - Công Nghệ

» Điện - Điện tử

Bài giảng Điều khiển số máy điện: Chương 3 - TS. Nguyễn Thanh Sơn

Chia sẻ: Caphesua | Ngày: | Loại File: PDF | Số trang:15

Báo xấu

25
lượt xem 1
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Điều khiển số máy điện: Chương 3 Các bộ điều khiển số cung cấp cho người học những kiến thức như: Các bộ điều khiển số; Bộ điều khiển Dahlin; Bộ điều khiển PID (PID controller). Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Điều khiển số máy điện: Chương 3 - TS. Nguyễn Thanh Sơn

Chương 3. Các bộ điều khiển số  Quy trình thiết kế các bộ điều khiển số gắn liền với việc xây dựng mô hình chính xác của quá trình (hay còn gọi là mô hình chính xác của đối tượng điều khiển).  Sau đó thuật toán điều khiển được phát triển để đạt được đáp ứng đầu ra theo mong muốn. 1 1 Chương 3. Các bộ điều khiển số Chúng ta có thể sử dụng một số phương pháp sau đây để thiết kế các hệ thống điều khiển số.  Xây dựng hàm truyền trong mặt phẳng p sau đó biến đổi hàm truyền sang miền z.  Hàm truyền của hệ thống được mô hình như là một hệ thống số và bộ điều khiển được thiết kế trực tiếp trong miền z. 2 2
Chương 3. Các bộ điều khiển số Quy trình thiết kế các bộ điều khiển số trong mặt phẳng z có thể được tóm tắt như sau:  Xác định hàm truyền của hệ thống sử dụng phương pháp toán học hoặc bằng cách phân tích phản ứng theo thời gian.  Biến đổi hàm truyền sang mặt phẳng z.  Thiết kế bộ điều khiển số trong mặt phẳng z.  Thực thi thuật toán điều khiển với máy tính số. 3 3 Chương 3. Các bộ điều khiển số 4 4
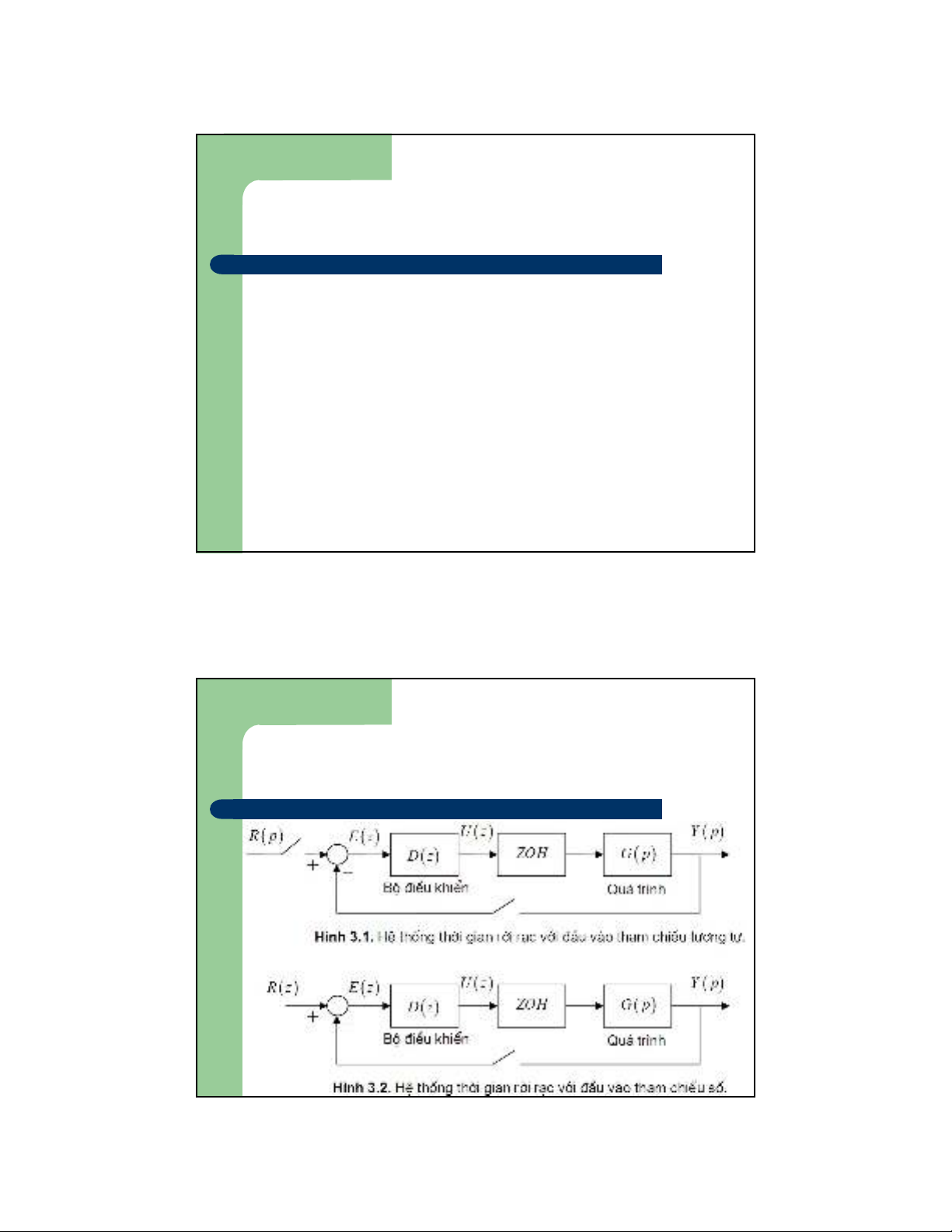
Chương 3. Các bộ điều khiển số 3.1 Các bộ điều khiển số 5 5 Chương 3. Các bộ điều khiển số 3.1 Các bộ điều khiển số Hàm truyền của hệ thống 3.3 có dạng như sau: Y z D  z  HG  z   (3.1) R  z  1  D  z  HG  z  Chúng ta ký hiệu hàm truyền của hệ kín T  z  có dạng như sau: Y z T z  (3.2) 6 R z 6
Chương 3. Các bộ điều khiển số 3.1 Các bộ điều khiển số Từ phương trình (3.1) và (3.2) ta xác định được hàm truyền của bộ điều khiển cần được thiết kế như sau: 1  T z  Dz    (3.3) HG  z  1  T  z   7 7 Chương 3. Các bộ điều khiển số 3.1 Các bộ điều khiển số  Phương trình (3.3) có nghĩa là chúng ta có thể thiết kế được bộ điều khiển số nếu biết được mô hình hay hàm truyền của quá trình.  Bộ điều khiển D  z  phải được thiết kế sao cho hệ là ổn định và có thể được thực thi bằng các phần cứng khác nhau. 8 8
Chương 3. Các bộ điều khiển số 3.1.1 Bộ điều khiển “dead-beat” Bộ điều khiển “dead-beat” là một bộ điều khiển mà đầu ra có dạng nhảy cấp như tín hiệu đầu vào nhưng trễ so với đầu vào một hoặc một vài chu kỳ lấy mẫu. T  z   z  k ở đây k  1 (3.4) 9 9 Chương 3. Các bộ điều khiển số 3.1.1 Bộ điều khiển “dead-beat” Từ phương trình (3.3), hàm truyền của bộ điều khiển cần được thiết kế có dạng như sau: 1  z k  Dz    (3.5) HG  z  1  z  k  10 10
Chương 3. Các bộ điều khiển số 3.1.1 Bộ điều khiển “dead-beat” Ví dụ 3.1: Thiết kế bộ điều khiển “dead-beat” cho hệ thống với đối tượng điều khiển có hàm truyền như sau: e 2 p G  p  1  10 p 11 11 Chương 3. Các bộ điều khiển số 3.1.1 Bộ điều khiển “dead-beat” Hàm truyền của hệ kín có dạng như sau: 1  e  pT   e2 p  HG  z   Z  G  p    1  z 1  Z    p   p 1  10 p   Giả thiết chu kỳ lấy mẫu T=1 giây ta có:  1/10  HG  z   1  z 1  z 2 Z   12  p 1/10  p   12
Chương 3. Các bộ điều khiển số 3.1.1 Bộ điều khiển “dead-beat” z 1  e0,1  1  e  0,1 HG  z   1  z 1  z  z  1 z  e  z 2 3   0,1 1  e 0,1 z 1 0, 095 z 3 HG  z   1  0,904 z 1 13 13 Chương 3. Các bộ điều khiển số 3.1.1 Bộ điều khiển “dead-beat” Do đó ta có 1  0, 904 z 1  z  k  Dz  0, 095 z 3 1  z  k  Giả thiết k  3 ta có 1  0, 904 z 1  z 3  z 3  0,904 z 2 D z   14 0, 095 z 3 1  z 3  0, 095  z 3  1 14
Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin Bộ điều khiển Dahlin là sự biến cải của bộ điều khiển “dead-beat” và tạo nên phản ứng theo hàm mũ trơn hơn phản ứng của bộ điều khiển “dead- beat”. 15 15 Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin Phản ứng yêu cầu của hệ thống trong mặt phẳng p có thể được viết như sau: 1  e  ap  Y  p    (3.6) p  1  pq  Trong đó a và q được chọn sao cho đáp ứng đầu ra theo mong muốn như trên hình 3.4. 16 16
Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin 17 17 Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin Dạng tổng quát của hàm truyền của bộ điều khiển Dahlin là: z  k 1  1  e q  T 1   Dz  (3.7) HG  z  1  e q z 1   1  e q z 1  z  k 1 T T     18 18
Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin Ví dụ 3.2: Thiết kế bộ điều khiển Dahlin cho một hệ thống với thời gian lấy mẫu T=1 giây và đối tượng điều khiển có dạng hàm truyền như sau: e 2 p G  p  1  10 p 19 19 Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin Theo ví dụ 3.1 ta có ta có hàm truyền của quá trình có dạng như sau: 0, 095 z 3 HG  z   1  0,904 z 1 Giả thiết chọn q  10 hàm truyền của bộ điều khiển có dạng như sau: 20 20
Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin 1  T z  Dz    HG  z  1  T  z   1  0,904 z 1 z  k 1 1  e0,1   0, 095 z 3 1  e 0,1 z 1  1  e 0,1 z 1  z  k 1 1  0,904 z 1 0, 095 z  k 1 D z  21 0, 095 z 3 1  0,904 z 1  0, 095 z  k 1 21 Chương 3. Các bộ điều khiển số 3.1.2 Bộ điều khiển Dahlin Giả sử k  2 ta có: 0, 095 z 3  0, 0858 z 2 Dz  0, 095 z 3  0, 0858 z 2  0, 0090 Tóm lại, với giả thiết hàm truyền của đối tượng đã biết trước chúng ta có thể xây dựng được hàm truyền của bộ điều khiển dễ dàng. 22 22
Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Đối với hệ thống không biết trước hàm truyền của đối tượng điều khiển chúng ta sử dụng bộ điều khiển tỷ lệ-tích phân-vi phân hay còn gọi là bộ điều khiển PID thường được sử dụng trong điều khiển quá trình. 23 23 Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Phương trình đầu ra của bộ điều khiển PID có dạng như sau:  1 t de  t   u  t   K p e  t    e  t  dt  Td  (3.8)  Ti 0 dt  Trong đó u  t  là đầu ra của bộ điều khiển, e  t  là tín hiệu sai lệch của bộ điều khiển, K p là hệ số tỷ lệ, Ti là thời gian tích phân, Td là thời gian 24 vi phân. 24
Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Biến đổi Laplace phương trình (3.8) ta có:  Kp  U  p   K p   K pTd p  E  p  (3.9)  Ti p   K  U  p    K p  i  Kd p  E  p  (3.10)  p  Kp Trong đó Ki  và K d  K p Td 25 Ti 25 Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Thành phần tỷ lệ: Sai lệch được nhân với hệ số K p được gọi là hệ số tỷ lệ. Nếu hệ số tỷ lệ lớn sẽ gây nên hiện tượng không ổn định và nếu hệ số tỷ lệ nhỏ sẽ làm cho hệ thống bị trôi. 26 26
Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Thành phần tích phân: Tích phân của sai lệch sẽ được thực hiện và được nhân với một hệ số Ki . Hệ số này được điều chỉnh để cho sai lệch là nhỏ nhất trong khoảng thời gian mong muốn. Nếu hệ số này quá lớn, hệ sẽ dao động. Nếu hệ số này quá nhỏ sẽ gây ra hiện tượng phản ứng chậm của hệ thống. 27 27 Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Thành phần vi phân: Vi phân của sai lệch sẽ được nhân với hệ số K d .Nếu hệ số này quá lớn hệ sẽ dao động. Nếu hệ số này quá nhỏ hệ sẽ ổn định lâu. 28 28
Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Biến đổi z của phương trình (3.9) có dạng như sau:  Kp T 1  z 1  U  z   K p  1  K pTd  E  z  (3.10)  Ti 1  z T  Trong đó T là chu kỳ lấy mẫu 29 29 Chương 3. Các bộ điều khiển số 3.2 Bộ điều khiển PID (PID controller) Nếu đặt K  a Kp K pTd p T b c Ti T thì hàm truyền của bộ điều khiển PID có dạng sau: U  z   aE  z   P  z   Q  z  (3.11) b Pz  E z (3.12) 1  z 1 30 Q  z   c 1  z 1  E  z  (3.13) 30

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí

65 tài liệu

2431 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.