Bài giảng Lý thuyết điều khiển tự động: Chương 4 - Khảo sát tính ổn định của hệ thống

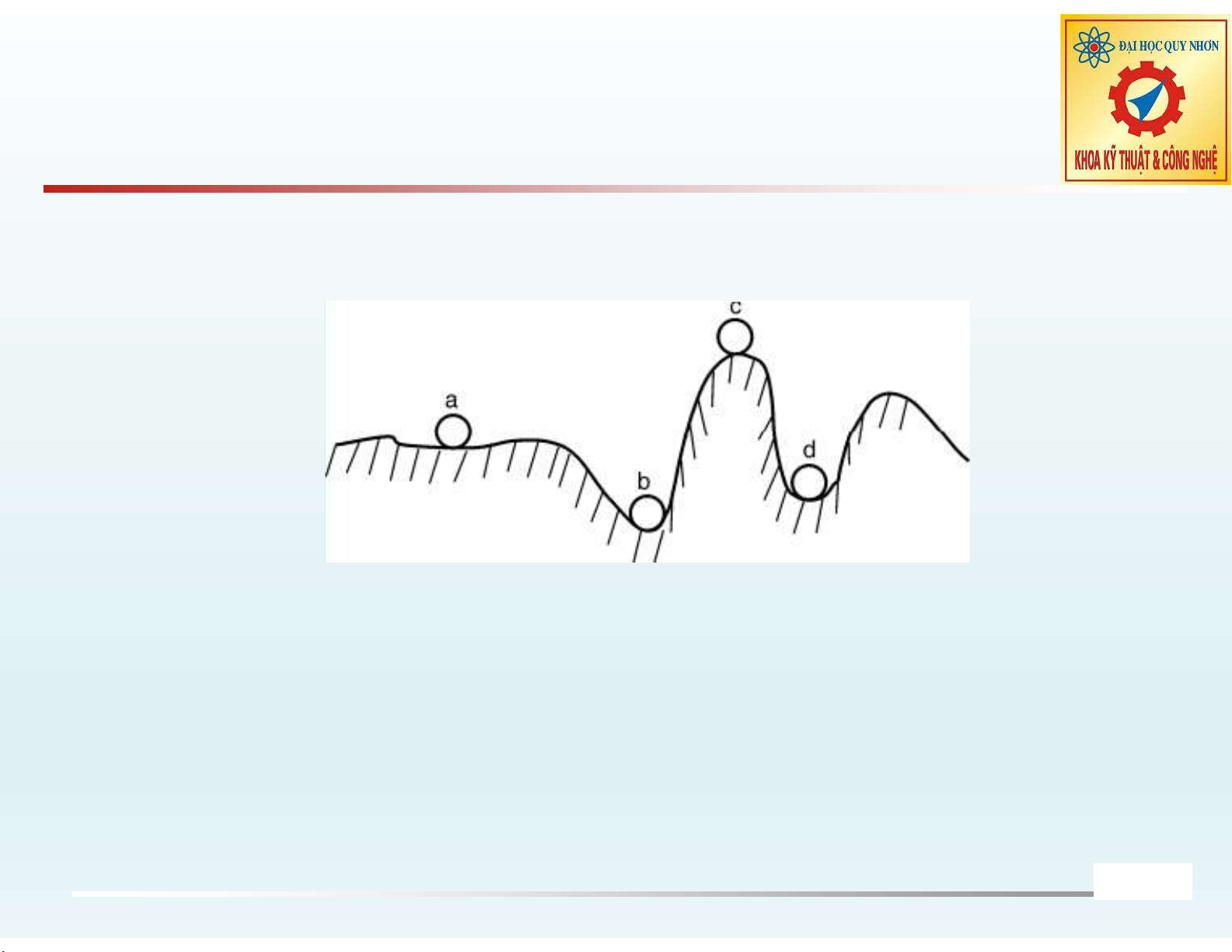
Trong kỹ thuật điều khiển, tính ổn định hệ thống là một yếu tố then chốt, quyết định khả năng vận hành an toàn và hiệu quả của mọi thiết bị hay quy trình. Một hệ thống không ổn định có thể dẫn đến hậu quả nghiêm trọng, từ mất kiểm soát đến hỏng hóc thiết bị. Do đó, việc phân tích và đảm bảo tính ổn định là yêu cầu bắt buộc trong thiết kế hệ thống điều khiển. Chương này tập trung trình bày các khái niệm cơ bản về ổn định và giới thiệu các phương pháp nền tảng để khảo sát tính ổn định của hệ thống, cung cấp kiến thức cần thiết để đánh giá hành vi động học của các hệ thống tự động, từ đó đưa ra quyết định thiết kế phù hợp nhằm đạt được hiệu suất mong muốn.

Sinh viên kỹ thuật, kỹ sư, và các nhà nghiên cứu trong lĩnh vực điều khiển tự động và hệ thống.

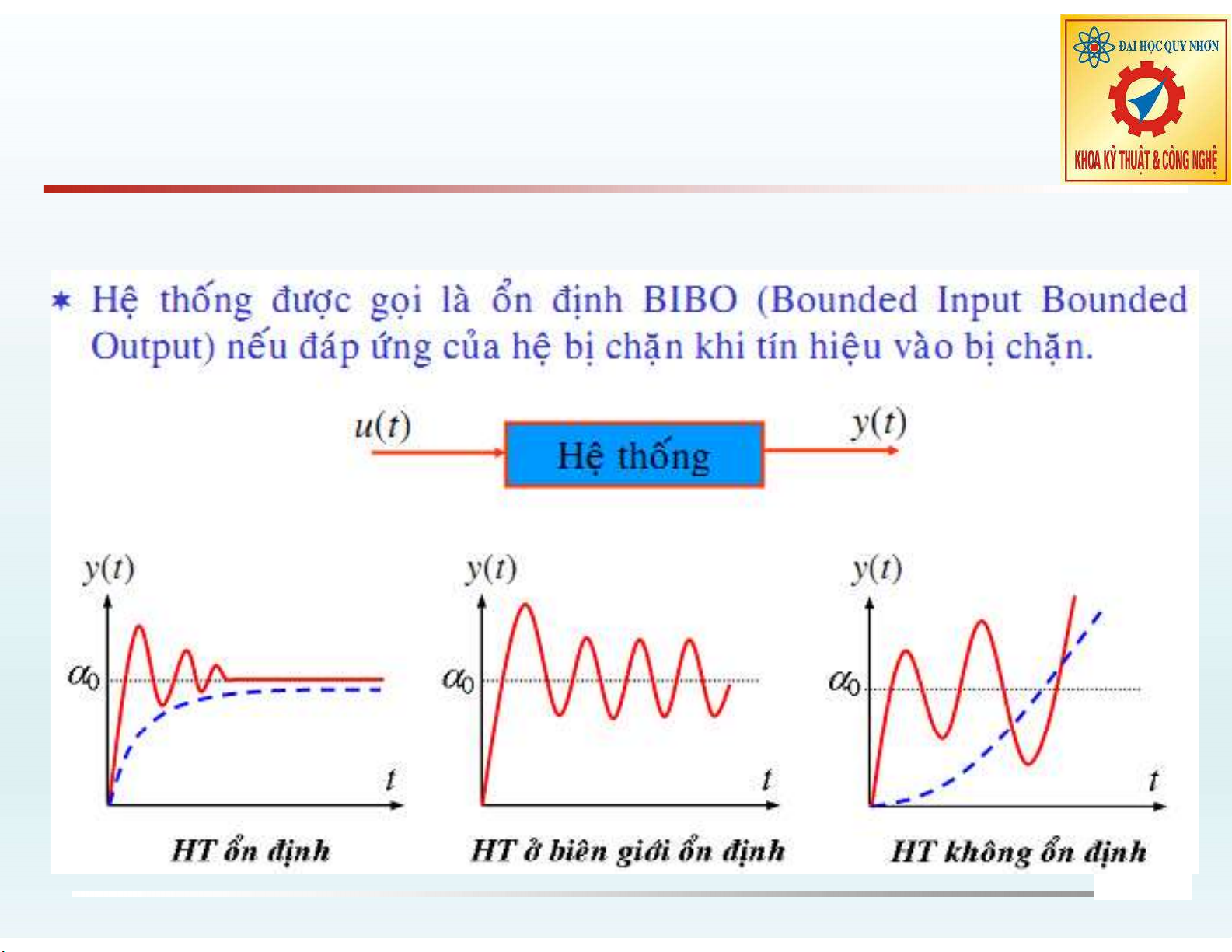
Tài liệu này cung cấp một cái nhìn toàn diện về tính ổn định hệ thống, một khía cạnh cơ bản trong phân tích và thiết kế hệ thống điều khiển. Chương bắt đầu bằng việc định nghĩa khái niệm về ổn định, bao gồm ổn định BIBO (Bounded Input Bounded Output), và làm rõ mối liên hệ giữa tính ổn định với vị trí của cực và zero của hệ thống trên mặt phẳng phức. Cụ thể, các điều kiện về vị trí của các cực (nằm bên trái mặt phẳng phức, trên trục ảo, hoặc bên phải mặt phẳng phức) được giải thích để xác định trạng thái ổn định, biên giới ổn định hay không ổn định của hệ thống. Khái niệm phương trình đặc trưng cũng được giới thiệu như một công cụ toán học để tìm các cực này. Trọng tâm của chương là trình bày chi tiết tiêu chuẩn ổn định đại số Routh-Hurwitz, một phương pháp mạnh mẽ để kiểm tra tính ổn định hệ thống mà không cần phải giải các nghiệm của phương trình đặc trưng. Tiêu chuẩn Routh-Hurwitz được giải thích qua hai phần chính: điều kiện cần (tất cả các hệ số của phương trình đặc trưng phải cùng dấu và khác 0) và qui tắc thành lập bảng Routh. Phương pháp này yêu cầu xây dựng một bảng Routh từ các hệ số của phương trình đặc trưng, sau đó kiểm tra các phần tử ở cột đầu tiên của bảng. Điều kiện đủ để hệ thống ổn định là tất cả các phần tử trong cột đầu tiên của bảng Routh phải dương. Số lần đổi dấu trong cột này cũng chỉ ra số lượng nghiệm nằm ở phần thực dương, cho biết mức độ không ổn định của hệ thống. Các ví dụ minh họa cụ thể giúp người đọc nắm vững cách áp dụng tiêu chuẩn Routh-Hurwitz để xác định tính ổn định hoặc tìm các tham số đảm bảo hệ thống hoạt động ổn định. Ngoài ra, tài liệu cũng liệt kê các phương pháp khác như phương pháp quỹ đạo nghiệm số và tiêu chuẩn ổn định tần số, mở ra các hướng nghiên cứu và ứng dụng tiếp theo trong phân tích động học và thiết kế hệ thống điều khiển phức tạp hơn.