1
1
ĐIỀU KHIỂN SỐ MÁY ĐIỆN
TS. Nguyễn Thanh Sơn
Viện Điện
ĐHBK Hà Nội
2
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.1 Tổng quan về các hệ thống điều khiển số
Các hệ thống điều khiển số hay còn gọi là các
hệ thống điều khiển với dữ liệu lấy mẫu làm
việc với các tín hiệu rời rạc theo thời gian.
Một máy tính số (vi điều khiển hoặc PC) sau khi
được lập trình có thể được sử dụng như là một
bộ điều khiển số.
1
2
2
3
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.1 Tổng quan về các hệ thống điều khiển số
4
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.2 Quy trình lấy mẫu và giữ mẫu
Một bộ lấy mẫu được xem như là một công
tắc đóng lại sau mỗi chu kỳ là T giây. Khi tín
hiệu liên tục ký hiệu là , thì tín hiệu rời
rạc đầu ra có dạng ký hiệu là
r t
*
( )
r t
3
4
3
5
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.2 Quy trình lấy mẫu và giữ mẫu
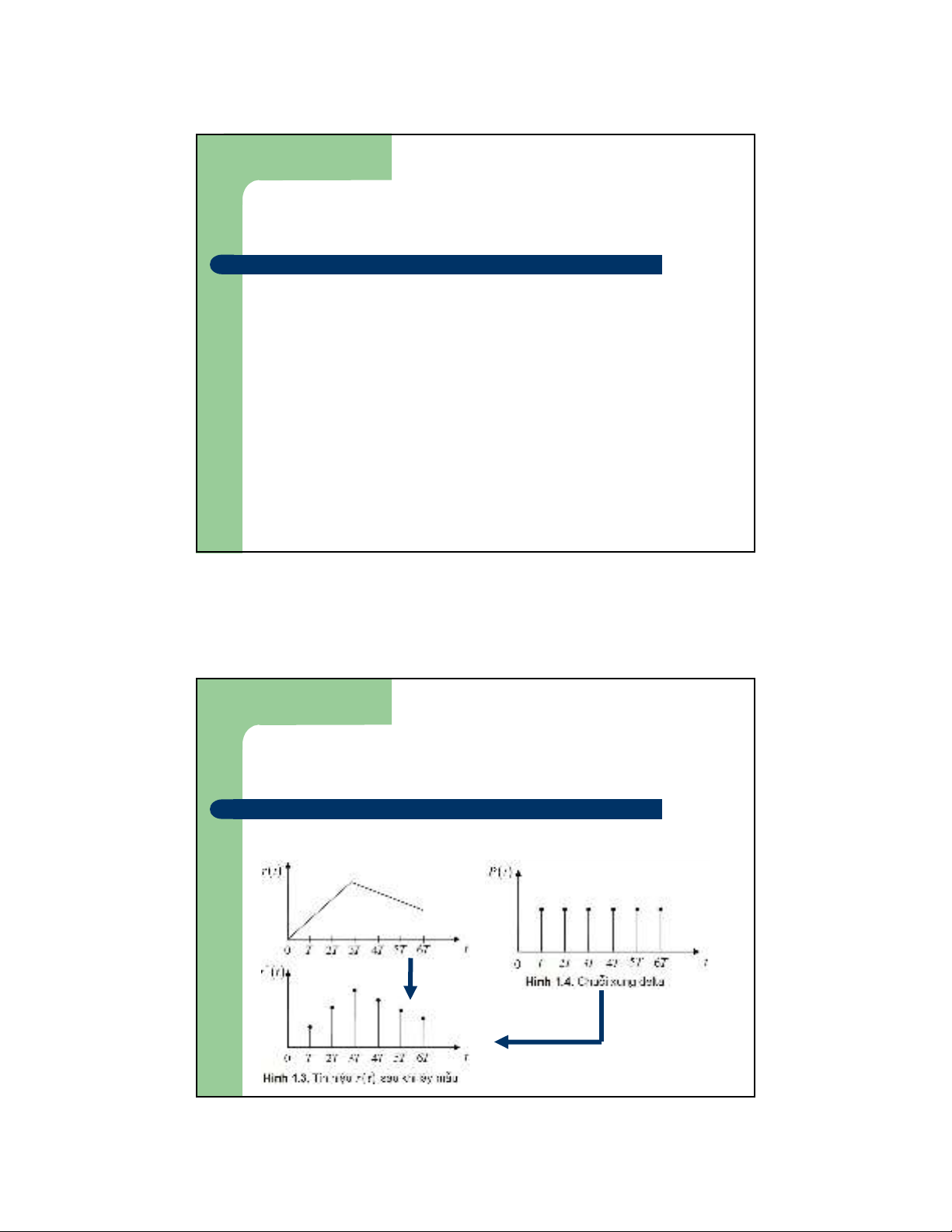
Một quá trình lấy mẫu lý tưởng có thể xem
như là tích của một chuỗi xung delta hay còn
gọi là xung đơn vị nhân với tín hiệu tương tự:
*
r t P t r t
(1.1)
Ở đây là xung delta hay là xung đơn vị.
P t
6
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.2 Quy trình lấy mẫu và giữ mẫu
5
6
4
7
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.2 Quy trình lấy mẫu và giữ mẫu
Xung delta được biểu diễn như sau:
n
P t t nT

(1.2)
*
n
r t r t t nT

Do đó ta có:
(1.3)
8
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.2 Quy trình lấy mẫu và giữ mẫu
hoặc:
(1.4)
Khi ta có nên:
0
t
0
r t
*
0n
r t r nT t nT
(1.5)
*
n
r t r nT t nT

7
8
5
9
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.2 Quy trình lấy mẫu và giữ mẫu
(1.5)
Biến đổi Laplace phương trình (1.5) ta có:
*
0n
r t r nT t nT
(1.6)
*
0
pnT
n
R p r nT e
Phương trình (1.6) đặc trưng cho biến đổi Laplace
tín hiệu liên tục được lấy mẫu
*
r t
10
Chương 1. Các hệ thống điều khiển số
và phép biến đổi z
1.2 Quy trình lấy mẫu và giữ mẫu
Một hệ thống lấy mẫu và giữ mẫu có thể được
xem như là sự kết hợp giữa bộ lấy mẫu và giữ
bậc không (Zero Order Hold/ZOH) như trên hình
1.5.
9
10