ĐỔI BIẾN TRONG TÍCH PHÂN BỘI BA
ĐỔI BIẾN TRONG TÍCH PHÂN BỘI BA
( , , )
( , , )
u y w
u v w
u v w
x x x
D x y z
J y y y
D u v w z z z
= =
f(x,y,z) xác định trong , đặt x = x(u,v,w)
y = y(u,v,w)
z = z(u,v,w)
(x,y,z) (u,v,w) ’
( , , ) ( , , ) | |f x y z dxdydz g u v w J dudvdw
Ω Ω
=
��� ���
Áp dụng vào việc xét tính đối xứng của
1
( , , )
2 ( , , )
f x y z dxdydz
f x y z dxdydz
Ω
Ω
=
���
���
Nếu gồm 2 phần 1 và 2 đối xứng nhau
qua mp z = 0
1.f chẵn theo z :
2.f lẻ theo z : ( , , ) 0f x y z dxdydz
Ω
=
���
Lưu ý:
• Mp z = 0 là mp Oxy
• Kết quả áp dụng tương tự nếu đối xứng
qua mp
• y = 0 (tính chẵn lẻ của f xét theo y)
• x = 0 (tính chẵn lẻ của f xét theo x)
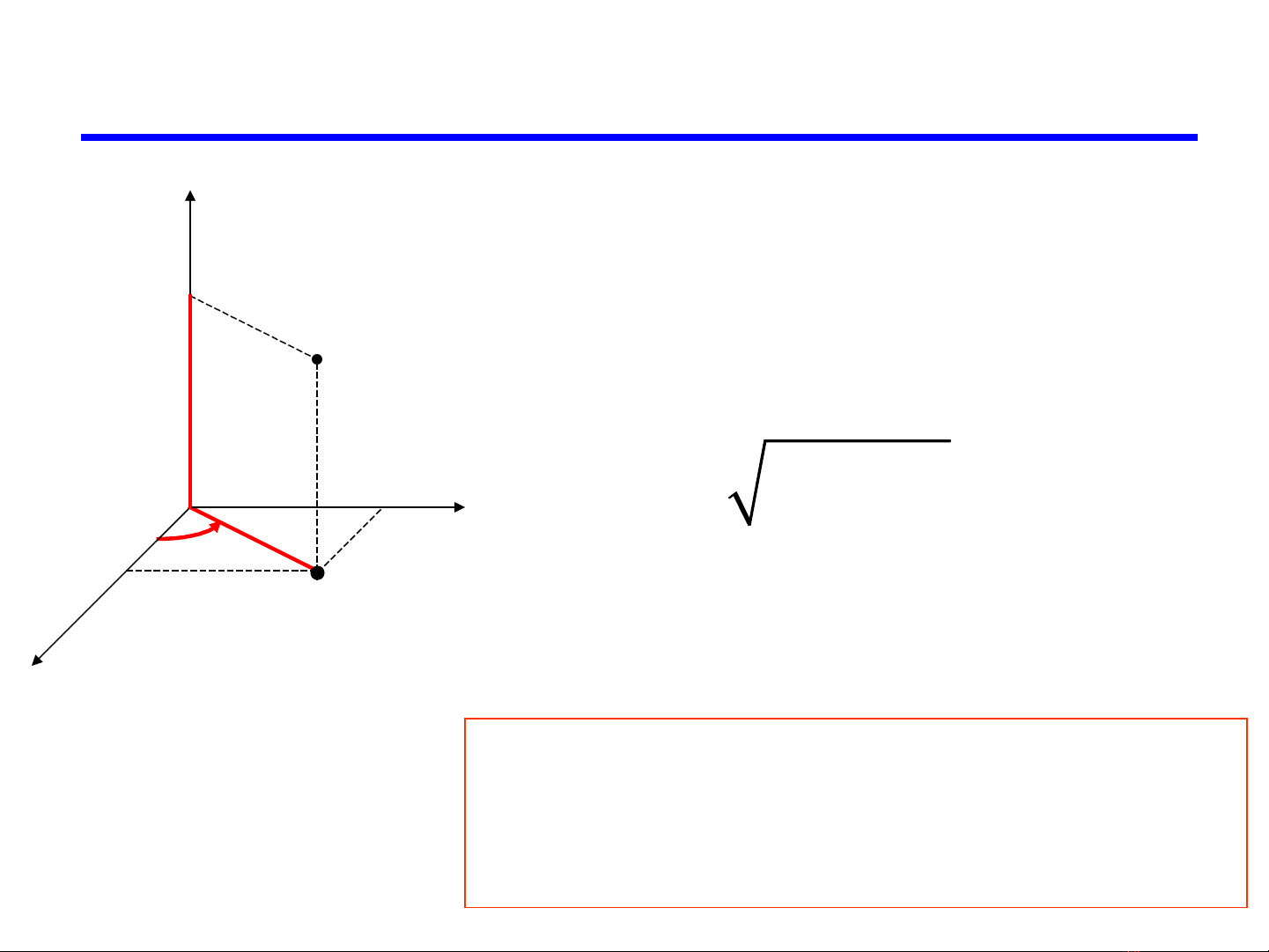
TỌA ĐỘ TRỤ
()
2 2
r x y= +
z
r
x
y
M
z
cố định z
M’
x = rcos, y = rsin, z = z
đổi sang tọa độ trụ
hình
chiếu D đổi sang tọa độ cực.