1
GIÁ TRỊTHEO THỜI GIAN
CỦA TIỀN TỆVÀ ỨNG DỤNG
VÀO PHÂN TÍCH DỰÁN
ĐẦU TƯ
Ph.D. NGUYỄN THỊLAN
1
2
NỘI DUNG CƠ BẢN
2
GIÁ TRỊTHỜI GIAN CỦA TiỀN TỆ
ỨNG DỤNG GIÁ TRỊTHỜI GIAN CỦA TiỀN TỆ
VÀO PHÂN TÍCH DỰÁN ĐẦU TƯ.
HOẠCH ĐỊNH NGÂN SÁCH TRONG ĐiỀU
KiỆN LẠM PHÁT.
3
•
I- GIÁ TRỊTHỜI GIAN CỦA TiỀN TỆ
Với cùng một lượng tiền nhận được, giá trị
của nó sẽkhông giống nhau nếu vào những
thời điểm khác nhau.
3
Cơ sở?
4
GIÁ TRỊTHỜI GIAN CỦA TiỀN TỆ
4
Giá trị tương lai của tiền tệ
Giá trịhiện tại (hiện giá) của tiền tệ
Các xác định giá trịhiện tại và tương lai của
các dòng tiền đặc biệt
5
GIÁ TRỊ TƯƠNG LAI CỦA TiỀN TỆ
GIÁ TRỊ TƯƠNG LAI CỦA MỘT SỐTiỀN
FVn=V0(1+ i)n
Trong đó:
FV: giá trị tương lai cho một khoản đầu tư hiện tại
V0: sốtiền đầu tư hiện tại
n: số năm đầu tư
i: tỷsuất sinh lợi hàng năm
• (1+ i)n là hệsốgiá trị tương lai
5
66
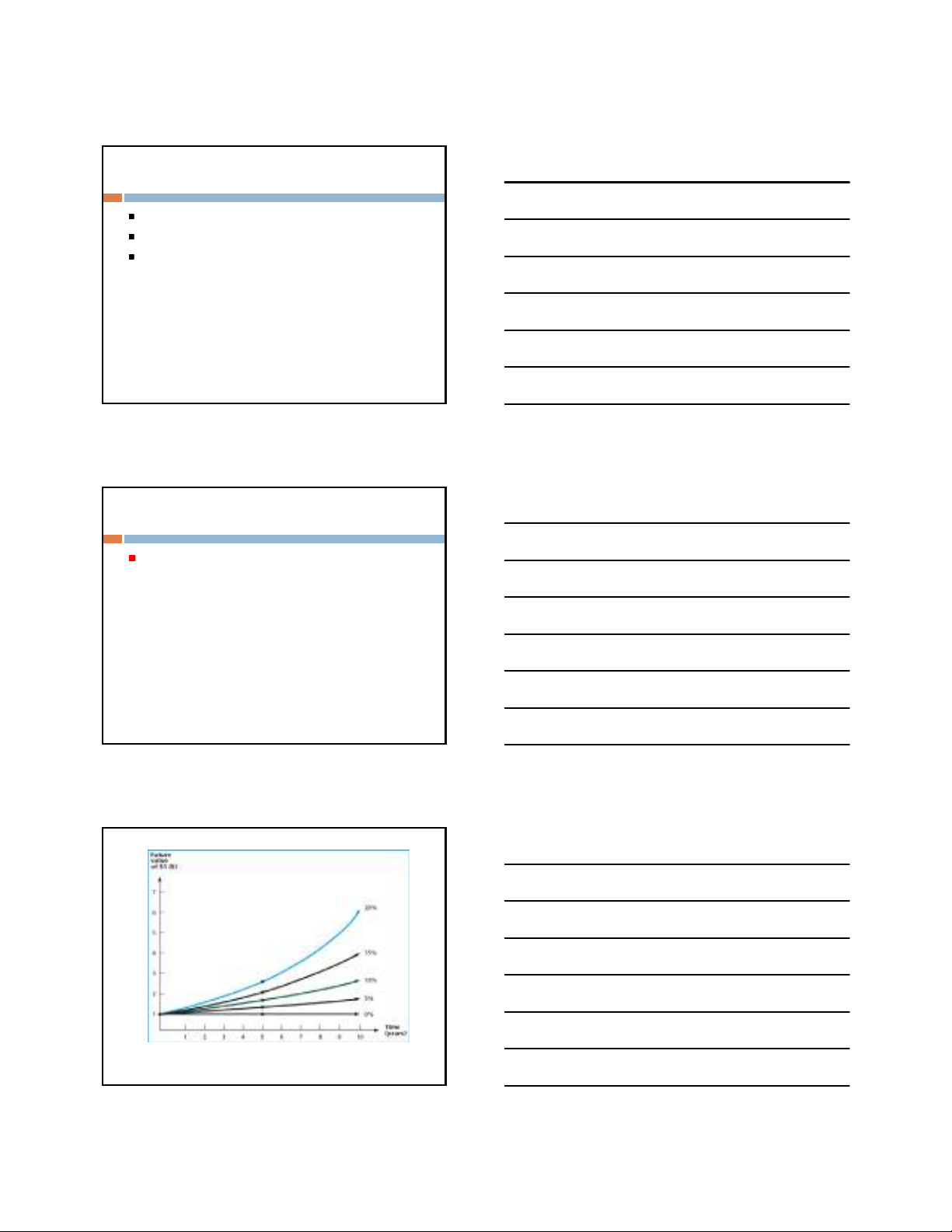
FV phụthuộc vào i và thời gian (t)
6
77
Mởrộng:
Tăng gấp đôi sốtiền đầu tư !→Quy tắc 72
Số năm cần thiết để một khoản đầu tư tăng
gấp đôi giá trịxấp xỉbằng 72/r, trong đór là
lãi suất tính theo năm.
Ví dụ:Gửi 100$ vào ngân hàng với lãi suất
10%/năm. Sau bao nhiêu năm, sốtiền sẽ tăng
gấp đôi?
7
8
GIÁ TRỊ TƯƠNG LAI CỦA TiỀN TỆ
GIÁ TRỊ TƯƠNG LAI CỦA CHUỖI TiỀN TỆ
Đối với chuỗi tiền tệ đầu kỳ:
8
V1V2V3Vn
n
n-1
3
210
Vn-1
n-2
Hay
)1()1(...)1()1( 2
1
1
21 iViViViVFV nn
nn ++++++++= −
−
∑
=
+−
+=
n
t
tn
tiVFV
1
1
)1(
9
GIÁ TRỊ TƯƠNG LAI CỦA TIỀN TỆ
GIÁ TRỊ TƯƠNG LAI CỦA CHUỖI TiỀN TỆ
Đối với chuỗi tiền tệcuối kỳ:
nn
nn ViViViVFV +++++++= −
−− )1(...)1()1( 1
2
2
1
1
V1V2V3Vn-1 Vn
n
n-1
3
210
∑
=
−
+=
n
t
tn
tiVFV
1
)1(
10
GIÁ TRỊHIỆN TẠI (HiỆN GIÁ) CỦA TIỀN TỆ
10
HIỆN GIÁ CỦA MỘT SỐTIỀN (TRONG TƯƠNG LAI)
Trong đó:
xr là mức lãi suất chiết khấu (discount rate)
xlà hệsốgiá trịhiện tại (hệsốchiết khấu)
Ví dụ:Ông A phải gửi 1 sốtiền vào NH là bao nhiêu để
sau 5 năm nữa ông A sẽnhận được 50.000.000 đ (biết
lãi suất NH là 10%/1năm).
n
n
n
n
r
FV
r
FV
PV )1(
1
)1( +
×=
+
=
n
r)1(
1
+
11
PV càng nhỏkhi thời gian càng dài
PV và r tỷlệnghịch với nhau
12
GIÁ TRỊHIỆN TẠI CỦA TiỀN TỆ
GIÁ TRỊHiỆN TẠI CỦA CHUỖI TiỀN TỆ
Đối với chuỗi tiền tệcuối kỳ:
Đối với chuỗi tiền tệ đầu kỳ:
12
∑
=+
×=
+
++
+
+
+
=
n
t
t
t
n
n
r
FV
r
FV
r
FV
r
FV
PV
1
2
21
)1(
1
)1(
...
)1()1(
∑
=
−
+=
n
t
t
trFVPV
1
)1(
∑
=
+−
+=
n
t
t
trFVPV
1
1
)1(
13
GIÁ TRỊHiỆN TẠI CỦA MỘT SỐDÒNG TiỀN ĐẶC BiỆT
13
Giá trịhiện tại của dòng niên kim (annuity)
Niên kim là dòng tiền cố định trong một thời gian nhất định
Trong đó:
xrlàlãi suất chiết khấu;
xC là sốtiền phải trả(hoặc nhận được) định kỳ;
xn là sốkỳ (năm) của dòng niên kim (kỳhạn của trái phiếu).
Ứng dụng: tính sốtiền phải trảgóp cố định theo định kỳ
và tính giá trịhiện tại của trái phiếu coupon.
)
)1(
1
1(
)1(
...
)1()1( 2
21
nn
n
rr
C
r
C
r
C
r
C
PV +
−×=
+
++
+
+
+
=
14
VÍ DỤ:Tính toán mức tiền phải trảkhi mua trả
góp hay thuê mua tài sản
Với: NG là sốtiền tài trợ ban đầu;at là sốtiền chi trả
trong kỳthứt
Trường hợp tiền trảdần đều vào cuối mỗi năm:
Trường hợp tiền trảdần đều vào đầu mỗi năm:
∑
=
−
+=
n
t
t
tiaNG
1
)1(
[]
n
i
i
a
NG −
+−×= )1(1
[]
n
i
i
ia
NG −
+−×
+
=)1(1
)1(
15
VÍ DỤ2:
Ông A mua trái phiếu của ngân hàng Liên Việt nhưng được trảtiền
trong 3 năm, mỗi năm nhận được 50 triệu. Như vậy, ông A nhận
được một khoản niên kim 50 triệu trong vòng 3 năm.
Công thức tính toán giá trịhiện tại của niên kim:
Với trường hợp trên, ông A sẽcó:
C= 50 triệu, n= 3 năm, với giả định tỷsuất chiết khấu là r =10%,
tương đương với các trái phiếu có cùng rủi ro và thời hạn trên thị
trường.
Sốtiền ông A bỏ ra để mua trái phiếu sẽlà:
PV = (50/0.1)x (1 – 1/1.13)=124.326 triệu.
)
)1(
1
1( n
rr
C
PV +
−×=