Chuỗi số
Khoa Khoa học Ứng dụng
Đại học Bách Khoa Thành phố Hồ Chí Minh
TĂNG LÂM TƯỜNG VINH
Tp. Hồ Chí Minh, 05/2020
TĂNG LÂM TƯỜNG VINH Chuỗi số 1 / 16
Nội dung
1Sơ đồ khảo sát sự hội tụ của chuỗi
2Các ví dụ
TĂNG LÂM TƯỜNG VINH Chuỗi số 2 / 16
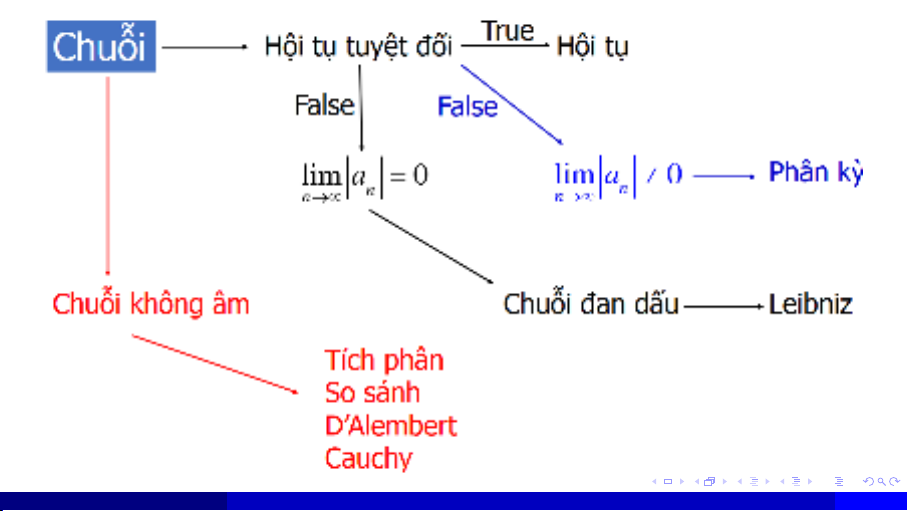
Sơ đồ các ví dụ mục bài
Bước 1: Khảo sát sự hội tụ tuyệt đối của chuỗi
◮Nếu chuỗi +∞
P
n=1
|an|hội tụ thì chuỗi +∞
P
n=1
anhội tụ.
◮Nếu chuỗi +∞
P
n=1
|an|phân kỳ do không thỏa mãn điều kiện cần lim
n→∞ |an| 6= 0thì lim
n→∞
an6= 0
⇒
+∞
P
n=1
anphân kỳ.
◮Nếu chuỗi +∞
P
n=1
|an|phân kỳ, nhưng thỏa mãn lim
n→∞ |an|= 0 thì ta chuyển sang bước 2.
Bước 2: Khảo sát sự hội tụ có điều kiện. Nếu chuỗi +∞
P
n=1
anlà chuỗi đan dấu →tiêu chuẩn Leibniz.
Bước 3: Khảo sát sự hội tụ của chuỗi không âm →tiêu chuẩn tích phân, so sánh, Cauchy, D’Alembert.
TĂNG LÂM TƯỜNG VINH Chuỗi số 3 / 16
TĂNG LÂM TƯỜNG VINH Chuỗi số 4 / 16
Chuỗi số xem lời giải các ví dụ mục bài
Ví dụ 1
Khảo sát sự hội tụ của chuỗi +∞
P
n=1
(−1)n+1
√n.
TĂNG LÂM TƯỜNG VINH Chuỗi số 5 / 16