intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Giải tích hàm nhiều biến – Chương 1: Đạo hàm và vi phân

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:107

Thêm vào BST
Báo xấu
60
lượt xem 8
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Giải tích hàm nhiều biến - Chương 1: Đạo hàm và vi phân" cung cấp cho người học các kiến thức: Các khái niệm cơ bản – Giới hạn và liên tục, đạo hàm riêng, khả vi và Vi phân, đạo hàm riêng và vi phân hàm hợp,... Mời các bạn cùng tham khảo.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Giải tích hàm nhiều biến – Chương 1: Đạo hàm và vi phân

  1. GIẢI TÍCH HÀM NHIỀU BIẾN • CHƯƠNG I: ĐẠO HÀM VÀ VI PHÂN • CHƯƠNG II : TÍCH PHÂN BỘI • CHƯƠNG III: TÍCH PHÂN ĐƯỜNG • CHƯƠNG IV: TÍCH PHÂN MẶT • CHƯƠNG V: CHUỖI SỐ - CHUỖI LŨY THỪA CuuDuongThanCong.com https://fb.com/tailieudientucntt
  2. CHƯƠNG I: ĐẠO HÀM VÀ VI PHÂN • §1: Các khái niệm cơ bản – Giới hạn và liên tục • §2: Đạo hàm riêng • §3: Khả vi và Vi phân • §4: Đạo hàm riêng và vi phân hàm hợp • §5: Đạo hàm riêng và vi phân hàm ẩn • §6: Công thức Taylor – Maclaurint • §7: Cực trị hàm nhiều biến : Cực trị tự do, cực trị có điều kiện, GTLN-GTNN trong miền đóng CuuDuongThanCong.com https://fb.com/tailieudientucntt
  3. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Định nghĩa hàm 2 biến : Cho D là tập con của R2 Hàm 2 biến f(x,y) là ánh xạ f : D → R ( x, y ) f ( x, y ) z Miền xác định của hàm là tất cả các giá trị của (x,y) làm biểu thức của hàm có nghĩa Miền giá trị của hàm là tập các giá trị mà hàm có thể nhận được CuuDuongThanCong.com https://fb.com/tailieudientucntt
  4. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Ví dụ : Tìm MXĐ, MGT của hàm f ( x, y ) 9 x2 y2 MXĐ là hình tròn D ( x, y ) R 2 : x 2 y2 9 MGT là đoạn [0,3] MXĐ 3 f(x,y) 3 0 3 (x,y) MGT CuuDuongThanCong.com https://fb.com/tailieudientucntt
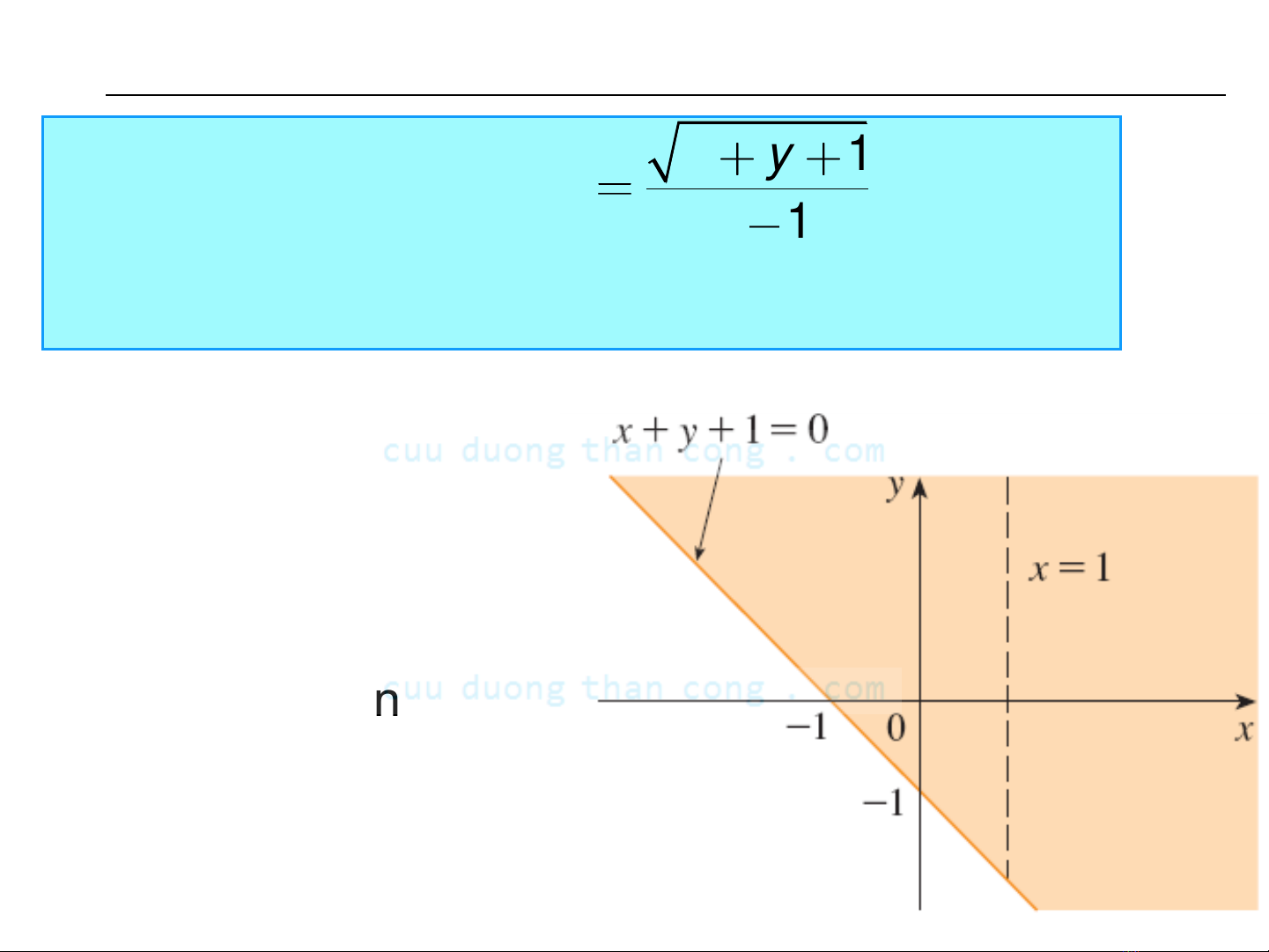
  5. §1 : Các khái niệm cơ bản – Giới hạn và liên tục x y 1 Ví dụ: Cho hàm f ( x, y ) x 1 Tính f(2,1) và tìm MXĐ của f Giải : a. f(2,1) = 2 b. MXĐ : Ta lấy nửa mặt phẳng phía trên đường thẳng x+y+1 = 0 và bỏ đi toàn bộ đường x = 1 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  6. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Cho f(x, y) là hàm 2 biến với MXĐ là D. Đồ thị của f là tập tất cả các điểm M(x, y, z)R3, với (x, y)D, z = f(x, y)  Đồ thị hàm z = f(x, y) là phần mặt S, khác với đồ thị hàm 1 biến y = f(x) là phần đường cong. CuuDuongThanCong.com https://fb.com/tailieudientucntt
  7. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Hình tròn mở tâm M0(x0,y0), bán kính r – kí hiệu B(M0,r) là tập 2 B(M0 , r ) M R : d (M , M 0 ) r 2 2 2 ( x, y ) R : (x x0 ) (y y0 ) r Hình tròn mở này còn được gọi là một r - lân cận của điểm M CuuDuongThanCong.com https://fb.com/tailieudientucntt
  8. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Cho tập D và 1 điểm M thuộc R2. Ta định nghĩa 3 loại điểm như sau : Điểm trong : M gọi là điểm trong của D nếu tồn tại ít nhất r>0 sao cho r- lân cận của M là B(M,r) nằm hoàn toàn trong D. Điểm biên : M gọi là điểm biên của D nếu với mọi r>0, hình cầu mở B(M,r) chứa những điểm thuộc D và những điểm không thuộc D. Điểm tụ : Điểm M gọi là điểm tụ của D nếu với mọi r>0, hình cầu mở B(M,r) đều chứa ít nhất 1 điểm N thuộc D, khác M CuuDuongThanCong.com https://fb.com/tailieudientucntt
  9. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Định lý : Điểm M là điểm tụ của tập D khi và chỉ khi tồn tại dãy điểm Mn (Mn≠M) tiến về M, tức là khi n→∞ thìd(Mn,M) →0 • Chú ý : 1. Như vậy điểm trong của D chắc chắn thuộc A, còn điểm biên của D thì có thể không thuộc D. 2. Điểm biên chắc chắn là điểm tụ, nhưng điểm tụ thì có thể không là điểm biên CuuDuongThanCong.com https://fb.com/tailieudientucntt
  10. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Tập D được gọi là tập đóng nếu D chứa mọi điểm biên của nó. Tập các điểm biên của D gọi là biên của D Tập D được gọi là tập mở nếu R2\D là tập đóng, khi đó, mọi điểm thuộc D đều là điểm trong, D không chứa bất kỳ điểm biên nào Tập D được gọi là tập bị chặn nếu nó được chứa trong một hình cầu nào đó, tức là r : D B(O, r ) Như vậy, có những tập chỉ chứa 1 phần biên mà không chứa toàn bộ biên nên sẽ là tập không mở, không đóng. CuuDuongThanCong.com https://fb.com/tailieudientucntt
  11. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Ví dụ : Cho D là phần hình cầu D ( x, y , z ) R 3 : x 2 y2 z2 4 Biên của D là toàn bộ mặt cầu x2 + y2 + z2 = 4, do đó D không chứa bất kỳ điểm biên nào tức là mọi điểm thuộc D đều là điểm trong. Vậy D là tập mở Ví dụ : Cho hình vành khăn D ( x, y ) R 2 : 1 x 2 y 2 4 Biên của D là 2 đường tròn x2 + y2=1 và x2+y2 = 4 nằm hoàn toàn trong D nên D là tập đóng CuuDuongThanCong.com https://fb.com/tailieudientucntt
  12. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Ví dụ : Trong R2 cho miền D D ( x, y ) R 2 : x y 3, x 0, y 0 Biên của D là 3 đoạn OA, OB, AB. Miền D không chứa đoạn AB tức là D B B không chứa mọi điểm biên nên D không là tập đóng. O A Tuy nhiên, D không là tập mở vì D chứa các điểm biên thuộc đoạn OA, OB Tập D là tập bị chặn vì ta có thể lấy đường tròn ngoại tiếp D chứa D (đường tròn tâm I là trung điểm AB, bán kính r = 1/2AB) tức là D nằm hoàn toàn trong 1 hình cầu mở CuuDuongThanCong.com https://fb.com/tailieudientucntt
  13. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Định nghĩa giới hạn hàm 2 biến : Cho hàm f(x,y) có miền xác định là D và M0(x0,y0) là 1 điểm tụ của D. Số a được gọi là giới hạn của hàm f khi x→x0, y→y0 (hay M →M0) nếu 0, 0 : ( x, y ) ( x0 , y 0 ),( x, y ) D, (x x0 )2 (y y 0 )2 f ( x, y ) a Khi ấy, ta viết M lim f (M ) M0 a hay lim f ( x, y ) x x0 a y y0 Lưu ý: Định nghĩa trên tương tự như giới hạn của hàm f(x), khi M dần đến M0 (không trùng M0), nếu f(M) dần về a thì ta cũng nói giới hạn của f(M) bằng a CuuDuongThanCong.com https://fb.com/tailieudientucntt
  14. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Một cách đơn giản hơn, ta định nghĩa giới hạn hàm cho riêng hàm 2 biến x, y theo đường cong như sau Khi điểm M dần đến M0 theo mọi đường cong L, mà hàm f(M) luôn dần về 1 giá trị a thì ta cũng có lim f (M ) a hay lim f ( x, y ) a M M0 x x0 y y0 Như vậy: Nếu M dần đến M0 theo 2 đường cong L1,L2 khác nhau và f(M) dần đến 2 giá trị a1≠a2 thìta nói không tồn tại giới hạn của hàm f(M) khi M→M0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  15. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Chú ý : Cách tìm giới hạn hàm 2 biến: Đưa về giới hạn hàm 1 biến hoặc dùng định lý kẹp xy 2 Ví dụ : Tính lim ( x ,y ) (0,0) x 2 y2 Giải : xy 2 0 2y Ta dùng định lý kẹp như khi x2 y 2 tính giới hạn hàm 1 biến: Suy ra giới hạn cần tìm bằng 0 CuuDuongThanCong.com https://fb.com/tailieudientucntt 0
  16. §1 : Các khái niệm cơ bản – Giới hạn và liên tục sin( xy ) Ví dụ : Tính lim ( x ,y ) (0,0) 1 3 1 xy Giải: Đặt t = xy →0 thì sin( xy ) sin t t lim lim lim 3 ( x ,y ) (0,0) 1 3 1 xy t 0 1 3 1 t t 0 1 t 3 Ví dụ : Tính xy lim x2 y 2 ( x ,y ) (0,0) Giải: Ta cho (x,y) →(0,0) theo 2 đường y = x và y = 2x Ta được x2 1 2x 2 2 lim 2 v? lim 2 ( x ,y ) (0,0) / y x 2x 2 ( x ,y ) (0,0) / y 2x 5x 5 Vậy giới hạn đã cho là không tồn tại CuuDuongThanCong.com https://fb.com/tailieudientucntt
  17. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Các tính chất giới hạn của tổng, tích, thương Cho lim f ( x, y ) a, lim g ( x, y ) b x x0 x x0 y y0 y y0 Ta có các kết quả sau khi x→x0, y→y0 1. lim(f(x,y)+g(x,y)=a+b 2. lim f(x,y).g(x,y) = a.b 3. lim C.f(x,y) = C.a f(x,y) a 4. lim ,b 0 g(x,y) b CuuDuongThanCong.com https://fb.com/tailieudientucntt
  18. §1 : Các khái niệm cơ bản – Giới hạn và liên tục Hàm liên tục : Hàm f(x,y) được gọi là liên tục tại (x0,y0) nếu f (x0,y0) xác định và lim f ( x, y ) f ( x0 , y 0 ) ( x ,y ) ( x0 ,y 0 ) Hàm liên tục trên miền D nếu nó liên tục tại mọi điểm thuộc miền D Tổng, tích, thương của 2 hàm liên tục là hàm liên tục Hợp của 2 hàm liên tục là một hàm liên tục Các hàm sơ cấp liên tục tại mọi điểm thuộc MXĐ CuuDuongThanCong.com https://fb.com/tailieudientucntt
  19. §2 : Đạo hàm riêng Định nghĩa đạo hàm riêng: Cho hàm 2 biến f(x,y), đạo hàm theo biến x của hàm f tại điểm (x0,y0) là giới hạn (nếu có) f f ( x0 x, y 0 ) f ( x0 , y 0 ) f x ( x0 , y 0 ) ( x0 , y 0 ) lim x x 0 x Tương tự, ta có định nghĩa đạo hàm riêng của hàm f theo biến y Quy tắc: Khi tính đạo hàm riêng của hàm f(x,y) theo biến x, ta coi y là hằng số CuuDuongThanCong.com https://fb.com/tailieudientucntt
  20. §2 : Đạo hàm riêng Ví dụ: Tính đạo hàm riêng của các hàm sau: a. f(x,y)= x 2 y 2 x cos y b. f(x,y)=e y c. f(x,y,z)=ln(x+e ) xyz Giải : x y a. fx , fy x2 y2 x2 y2 x x cos y x 1 cos y x x b. fx e ( s in ) , fy e ( s in )( 2 ) y y y y 1 ey c. fx y yz,fy y xz, fz xy x e x e CuuDuongThanCong.com https://fb.com/tailieudientucntt
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2