Bài giảng Giải tích hàm nhiều biến - Vũ Đỗ Huy Cường

Bài giảng này của giảng viên Vũ Đỗ Huy Cường thuộc khoa Toán-Tin học, Đại học Khoa học Tự Nhiên - TP. HCM, trình bày về giải tích hàm nhiều biến, bao gồm vi phân hàm nhiều biến và phương trình vi phân.

Bài giảng này phù hợp cho sinh viên đại học ngành toán hoặc các ngành kỹ thuật có sử dụng giải tích hàm nhiều biến.

Bài giảng này bao gồm hai chương chính: Vi phân hàm nhiều biến và Phương trình vi phân.

**Chương 1: Vi phân hàm nhiều biến**
* **Cơ sở và khái niệm:**
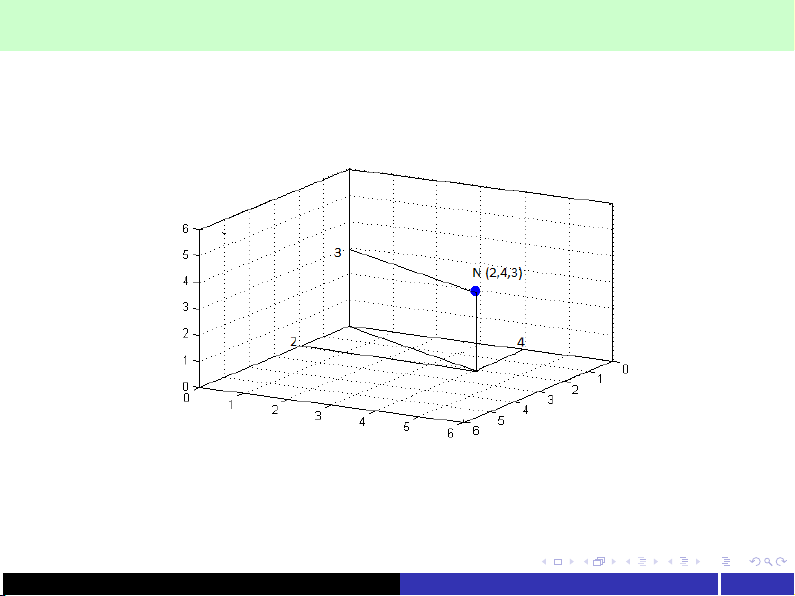
* Không gian IRn, định nghĩa và ví dụ về mặt phẳng Oxy và không gian Oxyz.
* Định nghĩa hàm nhiều biến, miền xác định và miền giá trị, kèm theo các ví dụ minh họa và bài tập.
* Đồ thị của hàm nhiều biến, phương pháp vẽ đồ thị, và bài tập về các đường cong và mặt cong.
* Đường mức và mặt mức, cùng bài tập vẽ đường mức.
* **Giới hạn và sự liên tục:**
* Giới hạn của hàm số, các phương pháp chứng minh giới hạn không tồn tại, và ví dụ minh họa.
* Sự liên tục của hàm số, định nghĩa, và bài tập kiểm tra tính liên tục.
* **Đạo hàm và vi phân:**
* Đạo hàm riêng phần, ký hiệu, quy tắc tính, và ví dụ minh họa.
* Đạo hàm riêng phần cấp cao, và ví dụ minh họa.
* Đạo hàm theo hướng, định nghĩa và công thức tính.
* Đạo hàm hàm hợp và hàm ẩn, định lý và ví dụ minh họa.
* Vi phân toàn phần, định nghĩa, công thức xấp xỉ, và ví dụ minh họa.
* Khai triển Taylor, công thức, và ví dụ minh họa.
* **Cực trị hàm hai biến:**
* Cực trị không có điều kiện, định nghĩa, điều kiện đủ, và ví dụ minh họa.
* Cực trị có điều kiện, phương pháp Lagrange, và ví dụ minh họa.
* Giá trị lớn nhất và giá trị nhỏ nhất của hàm hai biến trong miền đóng, các bước tìm kiếm và ví dụ minh họa.

**Chương 2: Phương trình vi phân**
* Định nghĩa phương trình vi phân, cấp của phương trình, nghiệm tổng quát và nghiệm riêng, bài toán Cauchy.
* Phương trình vi phân cấp 1, bao gồm phương trình tách biến và phương trình vi phân tuyến tính.