Hàm số liên tục
Đạo hàm Định nghĩa
Điểm gián đoạn
Nếu hàm số fkhông liên tục tại điểm athì ta gọi alà điểm
gián đoạn của f.
Phân loại điểm gián đoạn:
(i) Ta gọi alà điểm gián đoạn bỏ được/khử được nếu lim
x→a+f(x)
và lim
x→a−
f(x)tồn tại hữu hạn và bằng nhau.
(ii) Ta gọi alà điểm gián đoạn không bỏ được/không khử được
trong các trường hợp còn lại.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Hàm số liên tục
Đạo hàm Định nghĩa
Điểm gián đoạn
Định nghĩa
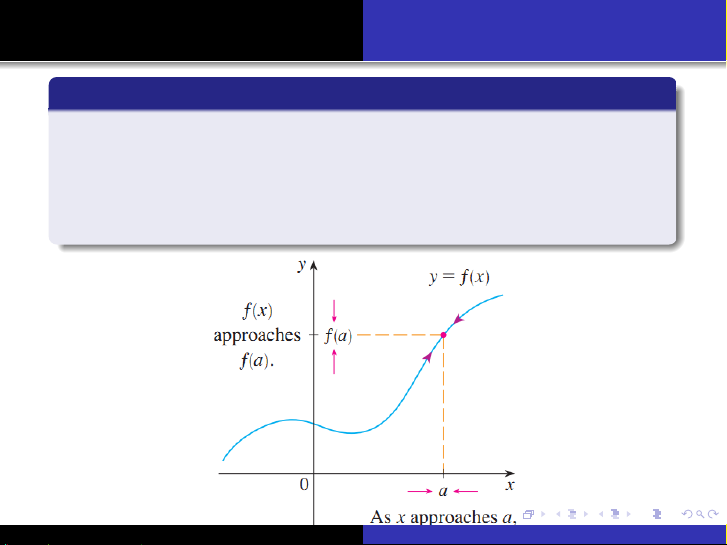
Hàm số fđược gọi là liên tục phải (continuous from the right)
tại điểm anếu
lim
x→a+f(x) = f(a),
và được gọi là liên tục trái (continuous from the left) tại điểm
anếu
lim
x→a−
f(x) = f(a).
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
