Khai triển Taylor
Hàm số cho bởi phương trình tham số
1Khai triển Taylor
Công thức và ý nghĩa
Khai triển Maclaurint một số hàm thường gặp
2Hàm số cho bởi phương trình tham số
Giới thiệu đường cong tham số
Đạo hàm của hàm số cho bởi phương trình tham số
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Khai triển Taylor
Hàm số cho bởi phương trình tham số Công thức và ý nghĩa
Khai triển Maclaurint một số hàm thường gặp
Cho hàm số fcó đạo hàm đến cấp ntrong một lân cận của
điểm cho trước x0.
Khai triển Taylor đến cấp ncủa hàm số f(x)trong lân cận
điểm x=x0là
f(x) = f(x0) + f0(x0)
1!(x−x0) + ··· +f(n)(x0)
n!(x−x0)n+Rn,
trong đó Rnlà phần dư (remainder) được xác định như
sau:
Rn=oh(x−x0)ni(dạng Peano).
Rn=f(n+1)(c)
(n+1)! (x−x0)n+1(dạng Lagrange), nếu fkhả vi đến
cấp n+1, và clà một điểm trung gian nào đó nằm trong lân
cận của x0.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Khai triển Taylor
Hàm số cho bởi phương trình tham số Công thức và ý nghĩa
Khai triển Maclaurint một số hàm thường gặp
Ý nghĩa của khai triển Taylor
Hàm số f(x)được xấp xỉ bởi những đa thức để thuận tiện cho việc
tính toán.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Khai triển Taylor
Hàm số cho bởi phương trình tham số Công thức và ý nghĩa
Khai triển Maclaurint một số hàm thường gặp
Công thức Maclaurint
Khai triển Taylor của hàm số f(x)trong lân cận điểm x=0 được
gọi là khai triển Maclaurint
f(x) = f(0) + f0(0)
1!x+··· +f(n)(0)
n!xn+o(xn),
trong đó o(xn)là VCB cấp cao hơn xnkhi x→0.
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)
Khai triển Taylor
Hàm số cho bởi phương trình tham số Công thức và ý nghĩa
Khai triển Maclaurint một số hàm thường gặp
(1) 1
1+x=1−x+··· + (−1)nxn+o(xn).
(2) ex=1+x
1!+··· +xn
n!+o(xn).
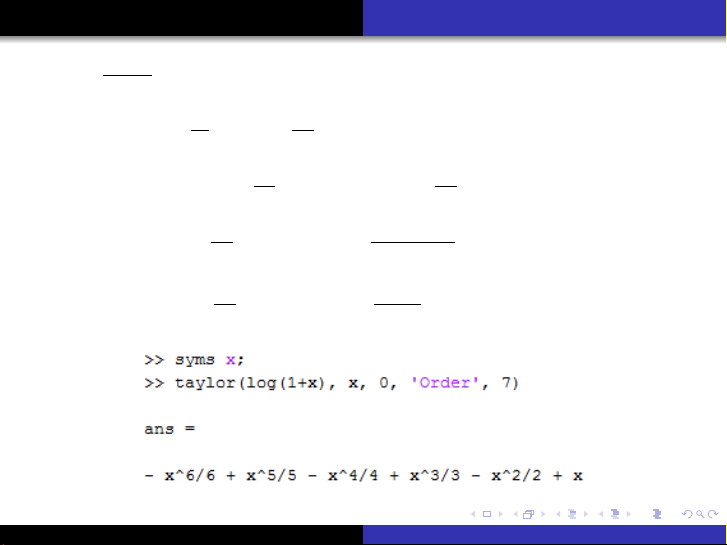
(3) ln(1+x) = x−x2
2+··· + (−1)n−1xn
n+o(xn).
(4) sin x=x−x3
3!+··· + (−1)nx2n+1
(2n+1)! +o(x2n+2).
(5) cos x=1−x2
2!+··· + (−1)nx2n
(2n)! +o(x2n+1).
TS. Đào Huy Cường (Bộ môn Toán Ứng Dụng) Giải tích 1 (Calculus 1)