TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI
VIỆN KỸ THUẬT HOÁ HỌC
BỘ MÔN HOÁ LÝ
Tên học phần: HOÁ LÝ
Mã học phần: CH3081
Giảng viên: Nghiêm Thị Thương-BM Hoá lý
Email: thuong.nghiemthi@hust.edu.vn
Văn phòng: 422-C1
GIỚI THIỆU MÔN HỌC
Mục tiêu học phần
1. Nắm vững khái niệm, điều kiện và các quy tắc cân bằng pha,
cân bằng điện ly
2. Áp dụng lý thuyết cân bằng pha, cân bằng điện ly vào các hệ
3. Có khả năng ứng dụng cân bằng pha, cân bằng điện ly trong
công nghệ, tính toán độ dẫn điện và các đại lượng nhiệt
động
4. Hiểu bản chất và quy luật của các hiện tượng bề mặt, các hệ
phân tán.Giải thích được các hiện tượng, tính chất này.
Giáo trình
1. Đào Văn Lượng (2000). Nhiệt động hóa học. NXB KH-KT.
2. Nguyễn Hữu Phú (2003). Hóa lý và Hóa keo. NXB KH-KT.
*Hệ là phần vật chất vĩ mô giới hạn để nghiên cứu, phần còn lại là môi trường
-Hệ cô lập: không trao đổi chất và năng lượng
-Hệ mở:trao đổi chất và trao đổi năng lượng
-Hệ kín: trao đổi năng lượng, không trao đổi chất
-Hệ đoạn nhiệt: không trao đổi nhiệt với MT bên ngoài
*Trạng thái:là tập hợp các thông số trạng thái mô tả tính chất của hệ
(T, P, d, m, V…)
*Hàm trạng thái:là hàm của thông số trạng thái
Ví dụ: U (nội năng), H (entanpy), S (entropy)…
*Quá trình:hệ chuyển từ trạng thái này sang trạng thái khác.
Quá trình thuận nghịch
#quá trình bất thuận nghịch
#quá trình 2 chiều
Hệ
Môi trường
CHƯƠNG 1. NHIỆT ĐỘNG HOÁ HỌC
1.1 Các khái niệm mở đầu
*Nhiệt và Công
Nhiệt Q:hình thức truyền năng lượng có liên quan sự thay đổi chuyển động hỗn loạn của
các phần tử trong hệ
Công A:hình thức truyền năng lượng có kèm theo chuyển dịch có hướng của một khối
lượng vĩ mô dưới tác dụng của một lực.
Công toàn phần A = công thể tích (công vô ích) + công có ích (A’)
Công thể tích =phần công nhường hoặc nhận khi thay đổi V
δA = PdV
Công có ích =phần công chuyển thành các dạng năng lượng có ích (công điện,công bề
mặt)
Quy ước dấu:Hệ nhận nhiệt Q>0; hệ toả nhiệt Q<0
Hệ sinh công A>0, hệ nhận công A<0
CHƯƠNG 1. NHIỆT ĐỘNG HOÁ HỌC
1.1 Các khái niệm mở đầu
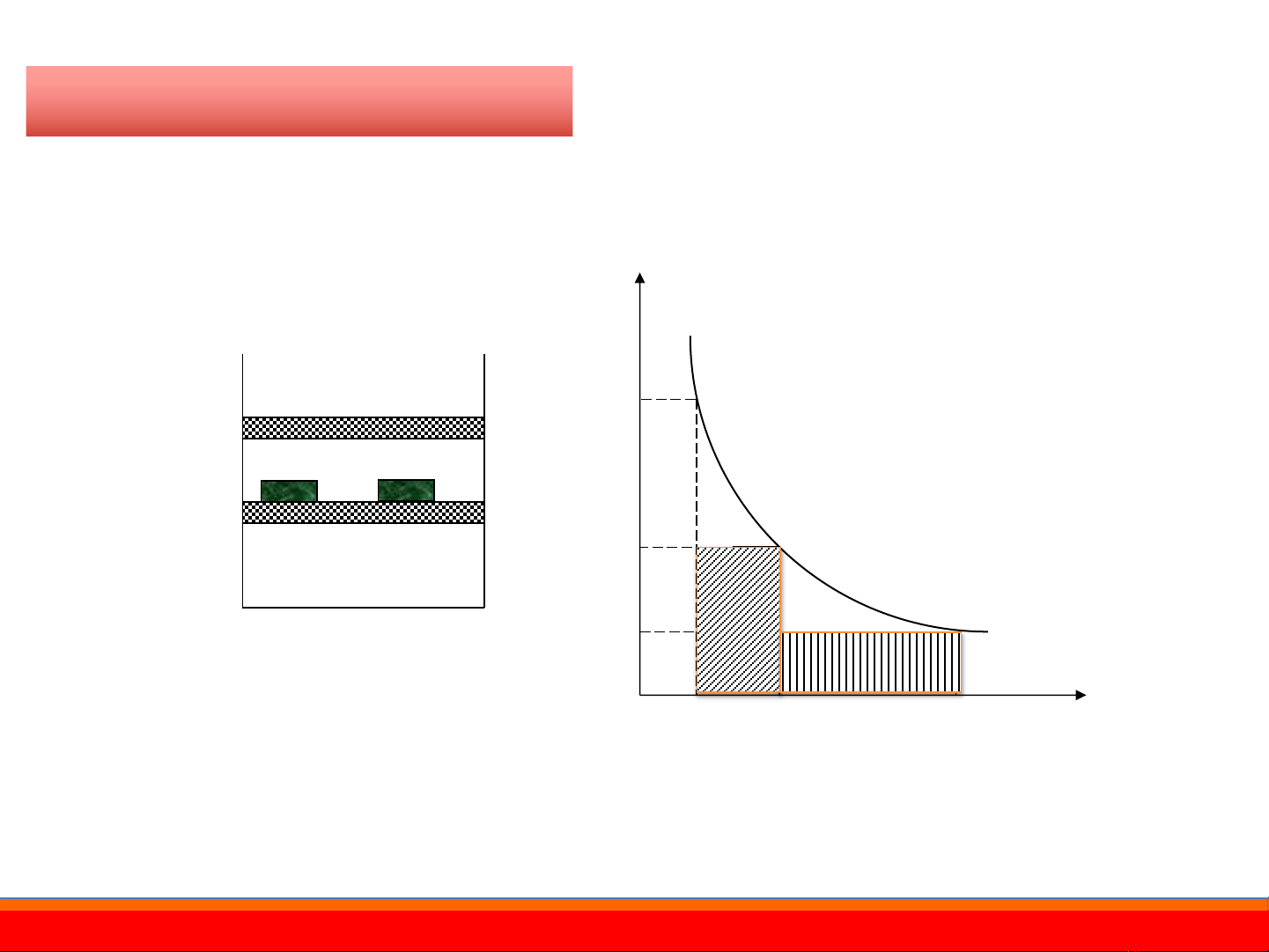
Công sẽ đạt giá trị cực đại khi tiến hành quá trình thuận nghịch
Khí
P1V1
P2V2
Piston PV=const
(1)
P1
P2
Pi
V1ViV2V
P
CHƯƠNG 1. NHIỆT ĐỘNG HOÁ HỌC
1.1 Các khái niệm mở đầu