5/13/2015 3:38 PM 1
Chương 2: ĐA CỘNG TUYẾN
Y
Y Y
Y
X1
X1
X1
X1
X2 X2
X2
X2
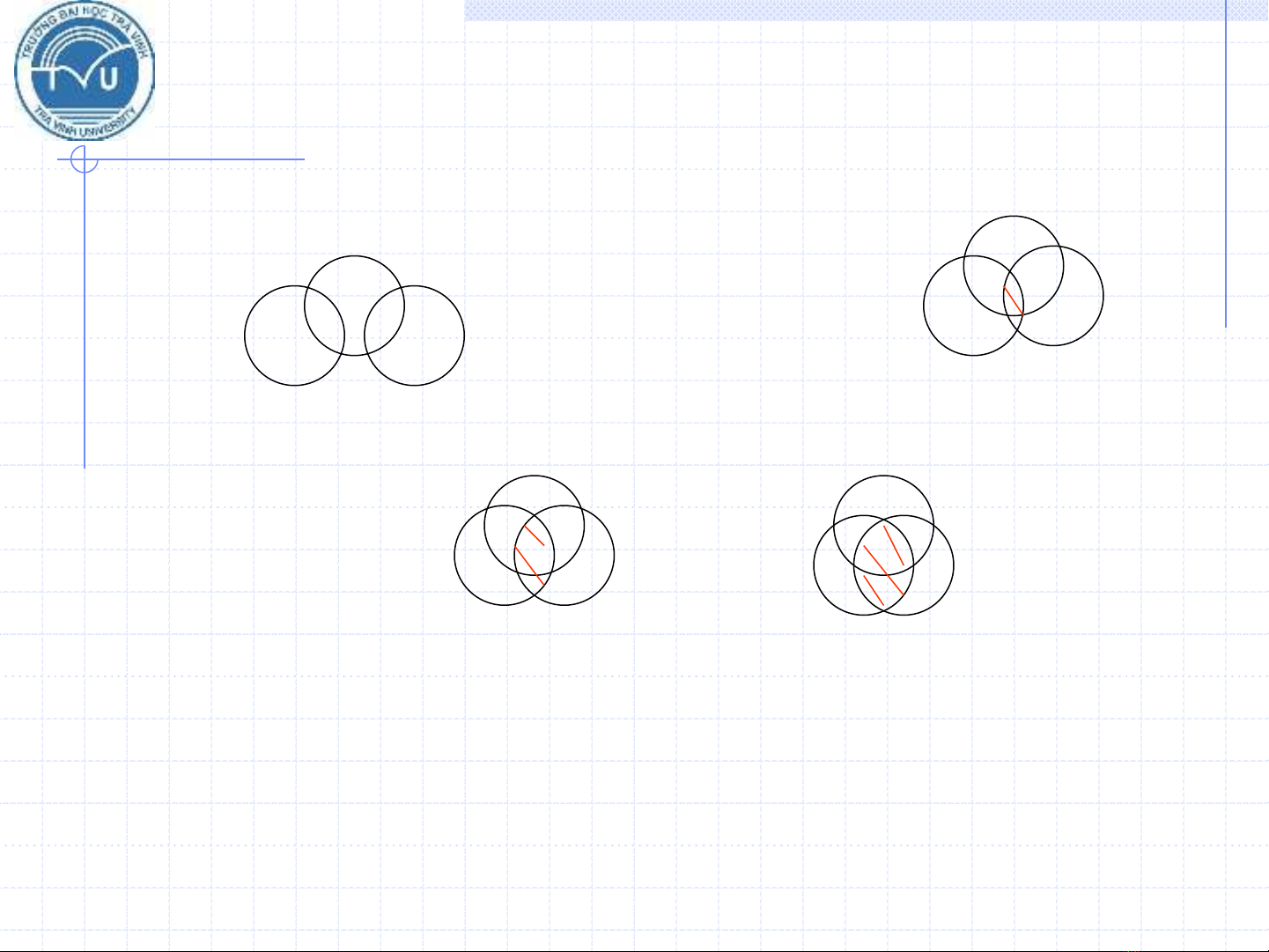
Hình 2.1. Biểu đồ Venn mô tả hiện tượng cộng tuyến
Đa cộng tuyến cao
Đa cộng tuyến thấp
Không có đa cộng tuyến
Đa cộng tuyến vừa
Xét mô hình: Yi = 1 + 2X2i + 3X3i + … + kXki + Ui
5/13/2015 3:38 PM 2
2.1. TỔNG QUAN VỀ ĐA CỘNG TUYẾN
Đa cộng tuyến là gì ?
Ragnar Frisch: Đa cộng tuyến có nghĩa là sự tồn
tại mối quan hệ tuyến tính “hoàn hảo” hoặc chính
xác giữa một số hoặc tất cả các biến giải thích
trong một mô hình hồi quy.
5/13/2015 3:38 PM 3
Xét hàm hồi quy tuyến tính k-1 biến độc lập:
Yi = 1 + 2X2i + 3X3i + … + kXki + Ui
Nếu tồn tại các số thực 2, 3, …… k sao cho:
2X2i + 3X3i + …… + kXki = 0
Với i ( i = 2, 3, k…) không đồng thời bằng không
thì giữa các biến Xi (i = 2, 3, …k) xảy ra hiện
tượng đa cộng tuyến hoàn hảo. Nói cách khác là
xảy ra trường hợp một biến giải thích nào đó được
biểu diễn dưới dạng một tổ hợp tuyến tính của các
biến còn lại.
2.1. TỔNG QUAN VỀ ĐA CỘNG TUYẾN
5/13/2015 3:38 PM 4
Nếu 2X2i + 3X3i + …… + kXki + vi = 0,
Với vi là sai số ngẫu nhiên thì ta có hiện tượng đa
cộng tuyến không hoàn hảo giữa các biến giải
thích. Nói cách khác là một biến giải thích nào đó
có tương quan với một số biến giải thích khác.
2.1. TỔNG QUAN VỀ ĐA CỘNG TUYẾN
5/13/2015 3:38 PM 5
Ví dụ
X3i = 5X2i, vì vậy có cộng tuyến hoàn hảo giữa X2 và
X3 ; r23 = 1
X2 và X3* không có cộng tuyến hoàn hảo, nhưng hai
biến này có tương quan chặt chẽ.
X2 10 15 18 24 30
X3 50 75 90 120 150
X*3 52 75 97 129 152