- Chæång II-
9/15/
2
Chæång 2
Tên hiãûu vaì phán têch tên hiãûu
Nhæ âaî giåïi thiãûu trong chæång træåïc, chæång naìy chuïng ta seî tçm hiãøu nhæîng neït chênh vãö tên
hiãûu vaì phæång phaïp phán têch tên hiãûu.
Tên hiãûu (signal) laì biãøu diãùn váût lyï cuía tin tæïc. Trong hãû thäúng truyãön tin, tên hiãûu nháûn âæåüc
thæåìng bao gäöm pháön chæïa tin tæïc mong muäún vaì pháön khäng mong muäún thãm vaìo. Pháön
mong muäún goüi laì tên hiãûu coï êch, pháön khäng mong muäún goüi laì nhiãùu (noise). Trong
chæång naìy giaí sæí tên hiãûu vaì nhiãùu âæåüc cäüng vaìo nhau åí bãn thu vaì goüi chung laì tên hiãûu.
Trong thæûc tãú coï thãø nhiãùu taïc âäüüng vaìo tên hiãûu bàòng caïch nhán vê duû nhæ fading.
Chæång naìy âæa ra caïc cäng cuû toaïn hoüc âãø biãøu diãùn tên hiãûu, trãn cå såí biãøu diãùn naìy tiãún
haình phán têch tên hiãûu âãø ruït ra caïc âàûc træng thêch håüp cho tên hiãûu tuìy theo caïc khêa caûnh
æïng duûng kyî thuáût khaïc nhau cuía noï.
Chæång naìy táûp trung giåïi thiãûu phæång phaïp phán têch thåìi gian, phán têch phäø (spectral
analysis) vaì phán têch tæång quan (correlation analysis).
Phán têch thåìi gian âæåüc hiãøu theo nghéa biãøu diãùn tên hiãûu trong miãön thåìi gian vaì trãn cå såí
âoï, tçm ra caïc âaûi læåüng âàûc træng cuía tên hiãûu nhæ nàng læåüng, cäng suáút, trë trung bçnh...
Phán têch phäø liãn quan âãún viãûc mä taí tên hiãûu trong miãön táön säú vaì mäúi liãn quan giæîa mä
taí trong miãön táön säú vaì miãön thåìi gian. Phán têch tæång quan åí cuäúi chæång daình âãø phán
têch tên hiãûu ngáùu nhiãn. Tên hiãûu trong thäng tin chênh laì loaûi tên hiãûu ngáùu nhiãn naìy.
2.1 Giåïi thiãûu
2.1.1 Âënh nghéa tên hiãûu
Tên hiãûu âæåüc âënh nghéa nhæ laì biãøu diãùn váût lyï cuía tin tæïc. Âoï laì mäüt âaûi læåüng váût lyï biãún
thiãn theo thåìi gian, khäng gian hay caïc biãún âäüc láûp khaïc. Vãö màût toaïn hoüc, coï thãø xem tên
hiãûu laì haìm theomäüt hoàûc nhiãöu biãún âäüc láûp. Vê duû nhæ, haìm
t
5)
t
(x
=
mä taí tên hiãûu thay âäøi tuyãún tênh theo biãún thåìi gian t. Hay haìm
2
y10xy2x3)y,x(s ++=
mä taí tên hiãûu theo hai biãún âäüc láûp x vaì y biãøu diãùn cho hai biãún khäng gian trong mäüt màût
phàóng.
Mäüt vê duû khaïc, tên hiãûu tiãúng noïi laì sæû thay âäøi aïp suáút khäng khê theo thåìi gian. Nhæng ta
khäng thãø biãøu diãùn tên hiãûu tiãúng noïi laì mäüt haìm theo thåìi gian maì täøng quaït, ta chè coï thãø
biãøu diãùn mäüt âoaûn (segment) tiãúng noïi nhæ laì täøng cuía nhiãöu haìm sin khaïc biãn âäü, táön säú vaì
pha nhæ sau:
- - 17
- Chæång II-
9/15/
2
∑
=
θ+π
N
1i iii )]t(t)t(F2sin[)t(A
Hçnh 2.1 laì mäüt vê duû vãö daûng soïng tên hiãûu tiãúng noïi - tæì tiãúng Anh "away"
Hçnh 2.1 Daûng soïng cuía tæì "away"
2.1.2 Phán loaûi tên hiãûu
Coï nhiãöu caïch khaïc nhau âãø phán loaûi tên hiãûu.
Trong mäüt vaìi æïng duûng, tên hiãûu coï thãø âæåüc taûo ra tæì nhiãöu nguäön hoàûc tæì nhiãöu bäü caím
biãún. Nhæîng tên hiãûu nhæ váûy âæåüc goüi laì tên hiãûu âa kãnh (multichannel signals). Vê duû nhæ,
tên hiãûu âiãûn tám âäö (ECG) 3 kãnh hoàûc 12 kãnh.
Xeït säú biãún âäüc láûp, ta tháúy coï nhæîng tên hiãûu laì haìm theo mäüt biãún âån, goüi laì tên hiãûu mäüt
hæåïng (one-dimensional signals), coï nhæîng tên hiãûu laì haìm theo M biãún (M > 1), goüi laì tên
hiãûu M-hæåïng (M-dimensional signals). Vê duû nhæ, tên hiãûu aính ténh laì tên hiãûu 2 hæåïng vç
aính laì haìm âäü saïng theo hai biãún khäng gian.
Xeït giaï trë cuía haìm, coï thãø giaï trë âoï laì mäüt giaï trë thæûc hay phæïc. Do âoï ta coï thãø phán loaûi
tên hiãûu thaình tên hiãûu thæûc hay phæïc.
Trong män hoüc naìy, ta chè xeït tên hiãûu thæûc, mäüt kãnh, mäüt hæåïng, biãún laì biãún thåìi gian. Ta
kyï hiãûu tên hiãûu naìy laì s(t) hay x(t).
Âãø coï thãø phán têch tên hiãûu, yãu cáöu ta phaíi mä taí âæåüc tên hiãûu bàòng mäüt mä hçnh toaïn hoüc
naìo âoï. Coï nhæîng tên hiãûu coï thãø xaïc âënh duy nháút bàòng mäüt mä hçnh toaïn hoüc quen thuäüc
nhæ laì baíng biãøu, âäö thë... Loaûi tên hiãûu naìy âæåüc goüi laì tên hiãûu xaïc âënh hay táút âënh
(deterministic signals). Loaûi tên hiãûu naìy âæåüc duìng âãø nháún maûnh ràòng ta coï thãø biãút roî táút
caí caïc giaï trë cuía tên hiãûu trong quaï khæï, hiãûn taûi vaì tæång lai.
Tuy nhiãn, thæûc tãú coï nhiãöu tên hiãûu maì ta khäng thãø mä taí chênh xaïc âæåüc. Do âoï khäng thãø
duìng mä hçnh toaïn hoüc quen thuäüc âãø biãøu diãùn tên hiãûu. Ta khäng thãø dæû âoaïn âæåüc haình vi
cuía loaûi tên hiãûu naìy. Ta goüi âáy laì tên hiãûu ngáùu nhiãn (random signals). Âãø biãøu diãùn loaûi
tên hiãûu naìy, ta phaíi dæûa vaìo caïc quan saït thäúng kã. Vê duû tên hiãûu tiãúng noïi, tên hiãûu nhiãùu laì
nhæîng tên hiãûu ngáùu nhiãn.
- - 18
- Chæång II-
9/15/
2
2.2 Biãøu diãùn tên hiãûu xaïc âënh theo thåìi gian
2.2.1 Tên hiãûu váût lyï vaì tên hiãûu toaïn hoüc
Tên hiãûu váût lyï (physical signals) laì tên hiãûu coï thãø thæûc hiãûn âæåüc vãö màût váût lyï (physically
realizable). Tên hiãûu váût lyï phaíi thoaí maîn caïc yãu cáöu sau:
- Coï giaï trë hæîu haûn, xaïc âënh trong mäüt khoaíng thåìi gian hæîu haûn
- Coï phäø hæîu haûn, xaïc âënh trong mäüt daíi táön säú hæîu haûn
- Laì haìm liãn tuûc theo thåìi gian
- Laì haìm thæûc
- Coï tênh nhán quaí, nghéa laì biãn âäü s bàòng 0 våïi thåìi gian t < 0.
Ngæåüc våïi tên hiãûu váût lyï laì tên hiãûu toaïn hoüc (mathematical signals). Âoï laì tên hiãûu chè coï yï
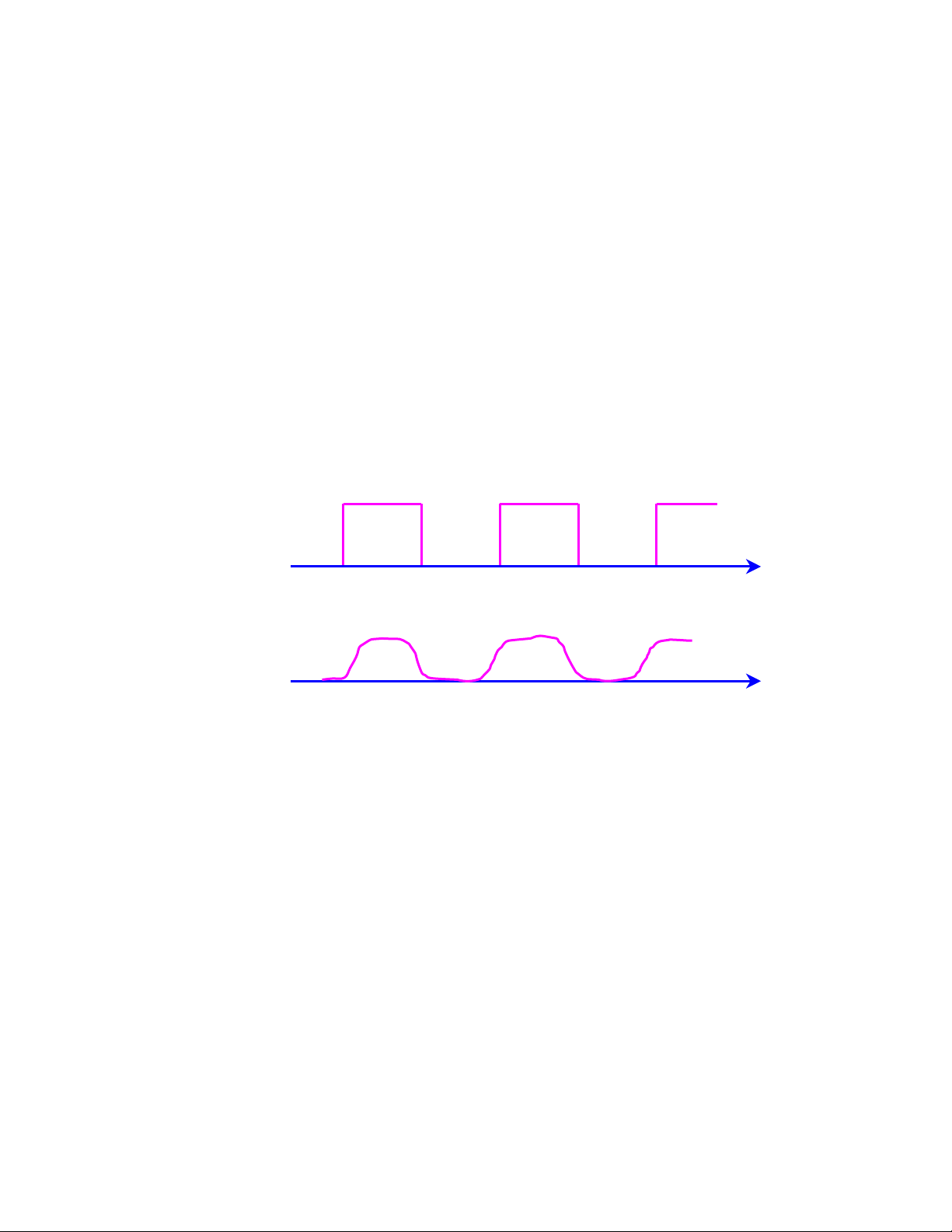
nghéa lyï thuyãút vaì hoaìn toaìn khäng thãø thæûc hiãûn âæåüc vãö màût váût lyï. Hçnh 2.2 âæa ra mäüt vê
duû vãö hai loaûi tên hiãûu xung vuäng váût lyï vaì toaïn hoüc.
-
t
t
(b)
(a)
Hçnh 2.2 Tên hiãûu xung vuäng váût lyï vaì toaïn hoüc
(a) Xung vuäng toaïn hoüc - (b) Xung vuäng váût lyï
2.2.2 Phán loaûi tên hiãûu dæûa theo daûng
Goüi kyï hiãûu biãøu diãùn tên hiãûu laì s(t), åí âáy s laì biãn âäü vaì t laì thåìi gian. Dæûa theo biãn âäü vaì
thåìi gian, ta coï thãø phán tên hiãûu thaình 4 loaûi:
Tên hiãûu liãn tuûc (continuous-time signals) hay tên hiãûu tæång tæû (analog signals) laì tên hiãûu
coï giaï trë xaïc âënh taûi moüi thåìi âiãøm tæì khi tên hiãûu sinh ra âãún khi kãút thuïc, nghéa laì caí biãn
âäü vaì thåìi gian âãöu liãn tuûc.
Tên hiãûu råìi raûc (discrete-time signals) laì tên hiãûu chè xaïc âënh taûi caïc giaï trë naìo âoï cuía thåìi
gian. Tên hiãûu naìy coï biãn âäü liãn tuûc vaì thåìi gian råìi raûc. Khoaíng caïch giæîa caïc thåìi âiãøm råìi
raûc khäng nháút thiãút phaíi bàòng nhau, nhæng trong thæûc tãú thæåìng khoaíng caïch naìy âæåüc láúy
bàòng nhau. Coï thãø taûo ra tên hiãûu råìi raûc bàòng hai caïch. Mäüt laìì láúy máùu tên hiãûu liãn tuûc, âáy
laì caïch thäng thæåìng âãø chuyãøn tên hiãûu tæì liãn tuûc thaình råìi raûc. Hai laì âo (âãúm) mäüt âaûi
- 19
- Chæång II-
9/15/
2
læåüng naìo âoï theo mäüt chu kyì nháút âënh, vê duû nhæ cán em beï theo tæìng thaïng, âo aïp suáút
khäng khê theo giåì...
Tên hiãûu læåüng tæí hoïa (quantization signals) laì tên hiãûu chè coï táûp hæîu haûn säú mæïc biãn âäü,
nghéa laì biãn âäü råìi raûc vaì thåìi gian liãn tuûc. Vê duû nhæ tên hiãûu ra cuía bäü giæî máùu báûc khäng
ZOH.
Tên hiãûu säú (digital signals) laì tên hiãûu råìi raûc coï biãn âäü âæåüc råìi raûc hoïa, nghéa laì caí biãn âäü
vaì thåìi gian âãöu råìi raûc.
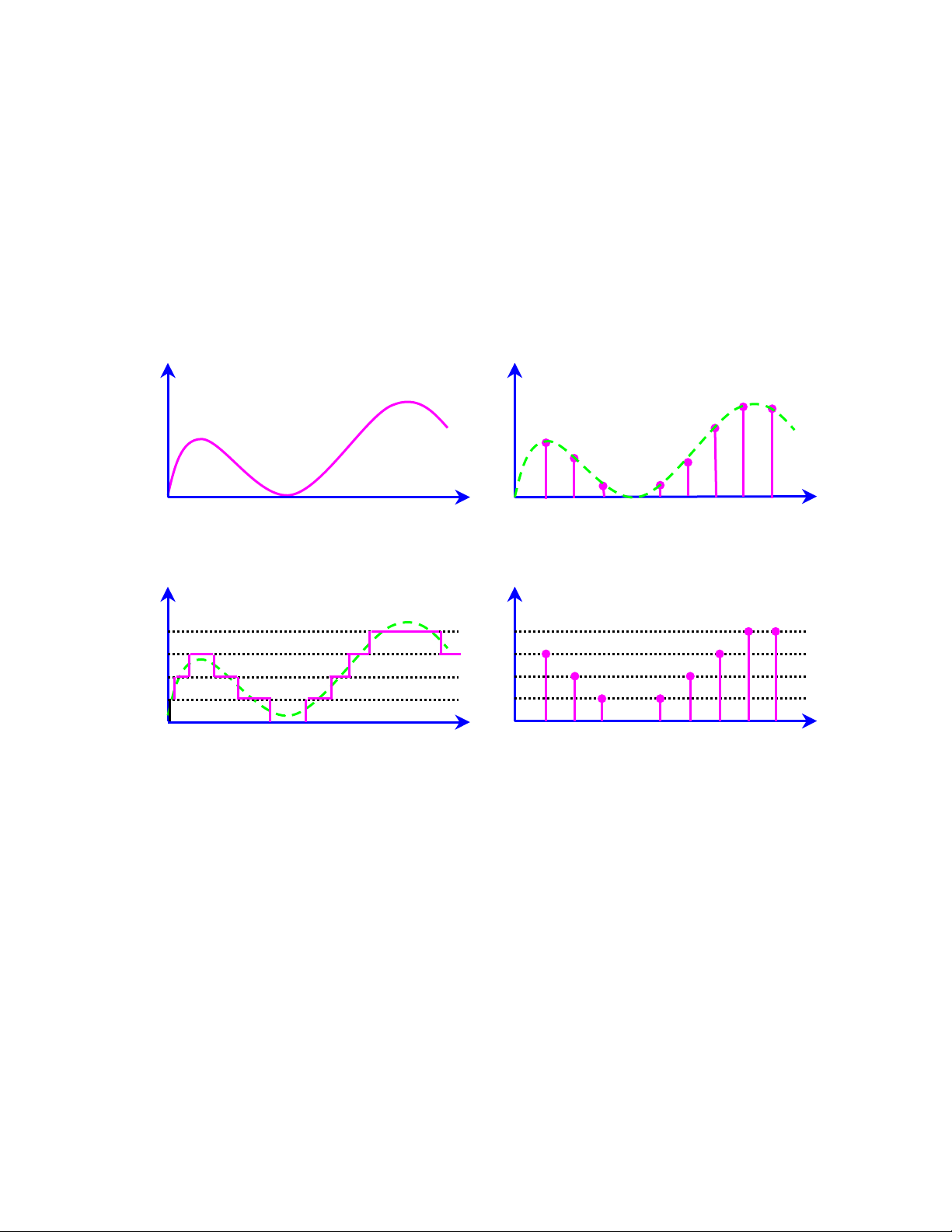
Hçnh 2.3 laì âäö thë cuía 4 loaûi tên hiãûu trãn.
•
•
•
•
(b)
(d)
(a)
(c)
Hçnh 2.3 Âäö thë bäún loaûi tên hiãûu
(a) Liãn tuûc - (b) Råìi raûc - (c) Læåüng tæí hoïa - (d) Säú
2.2.3 Caïc tên hiãûu toaïn hoüc cå baín
- Tên hiãûu (delta) Dirac laì tên hiãûu âæåüc âënh nghéa båíi:
)0(sdt)t()t(s =δ
∫
∞
∞−
våïi s(t) laì haìm liãn tuûc taûi t = 0. Ngoaìi ra coìn coï âënh nghéa khaïc cho tên hiãûu Dirac laì:
1dt)t( =δ
∫
∞
∞−
- - 20
- Chæång II-
9/15/
2
vaì
⎩
⎨
⎧
≠
=
∞
=δ 0t,0
0t,
)t(
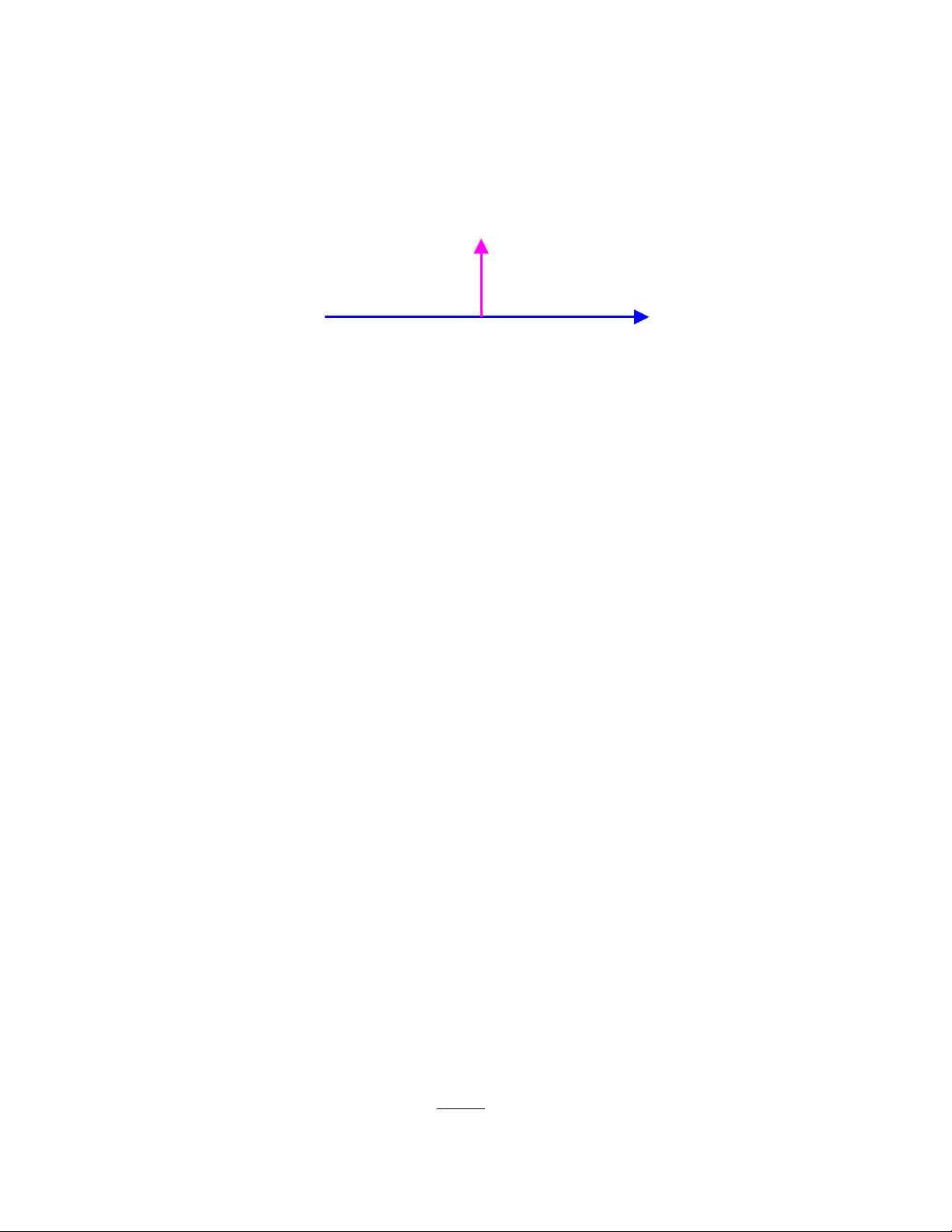
Âäö thë cuía tên hiãûu Dirac nhæ hçnh 2.4.
-
Hçnh 2.4 Tên hiãûu Dirac
1
0
Tên hiãûu Dirac âæåüc chæïng minh laì coï mäüt säú tênh cháút cuía nhæ:
)t(sdt)tt()t(s 00 =−δ
∫
∞
∞−
)t(sdt)t()tt(s 00 =δ+
∫
∞
∞−
)
t
(A)
t
(A
δ
=
−
0
t
khi,0)
t
(A
≠
=
)tt()BA()tt(B)tt(A 000
−
δ
+
=
−
δ
+
−δ
Våïi y(t) liãn tuûc taûi t0 ta coï: )tt()t(Ay)]tt(A)[t(y 000
−
δ
=
−
δ
,tt2j dte)t(
,
∫
∞
∞−
π±
=δ
-Tên hiãûu bæåïc nhaíy âån vë (unit step) laì tên hiãûu:
⎩
⎨
⎧
<
>
=0t,0
0t,1
)t(u
Tæì âënh nghéa coï thãø suy ra mäúi quan hãû giæîa tên hiãûu Dirac vaì tên hiãûu bæåïc nhaíy âån vë nhæ
sau:
∫
∞−
=λλδ
t
)t(ud)(
vaì
)t(
dt
)t(du δ=
- 21