Giới thiệu tài liệu
Bài giảng này chủ yếu mô tả về phương pháp Toán tử Laplace và các ứng dụng của nó trong lý thuyết mạch điện. Nó giúp học viên có thể hiểu rõ quy tắc chung về hệ thống điện và sử dụng phương pháp này để giải quyết vấn đề trong lĩnh vực mạch điện.
Đối tượng sử dụng
Nhóm người sẽ lợi dụng bài giảng này là học viên, doanh nghiệp có quan tâm về mạch điện và các yếu tố liên quan.
Nội dung tóm tắt
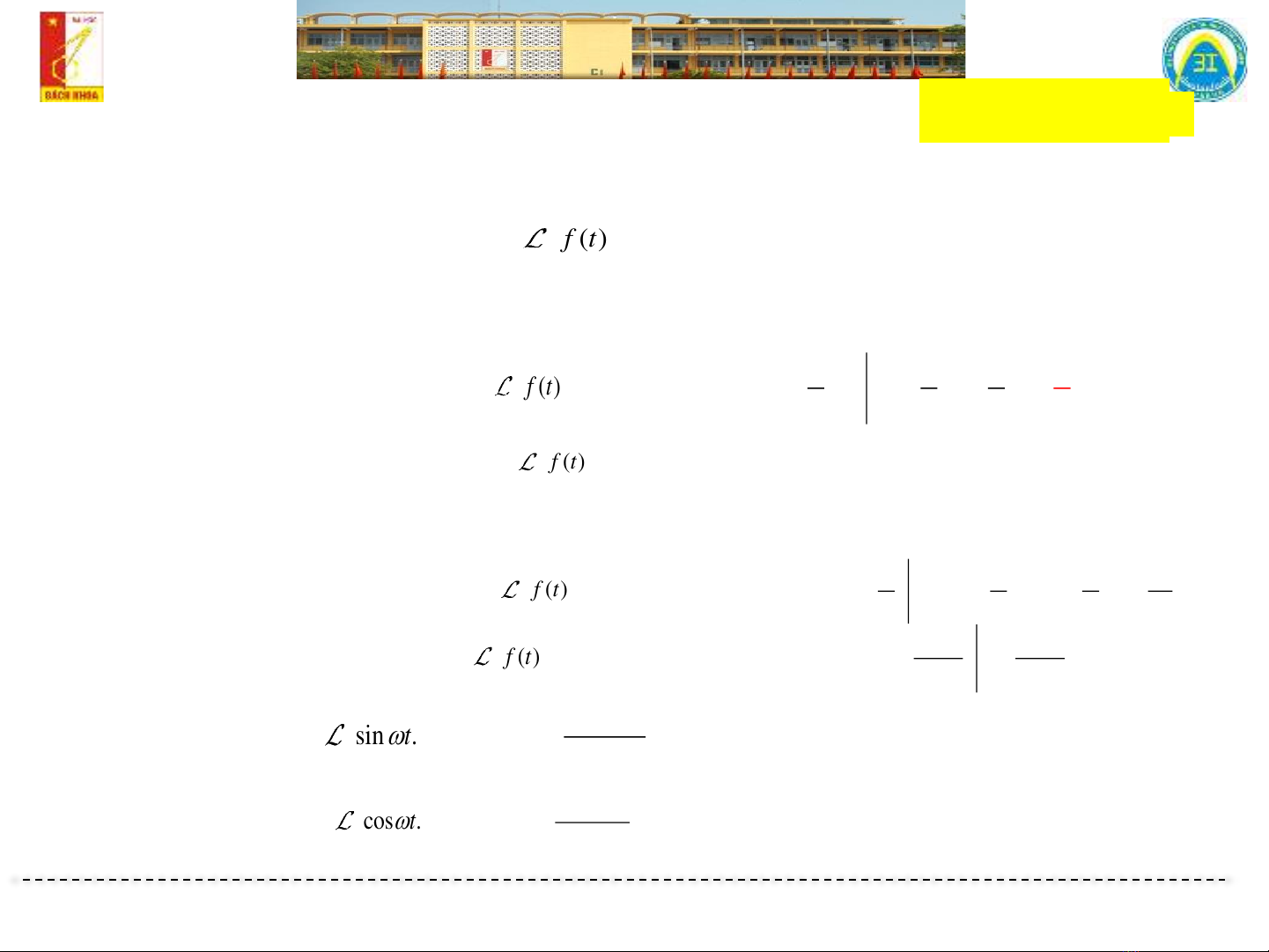
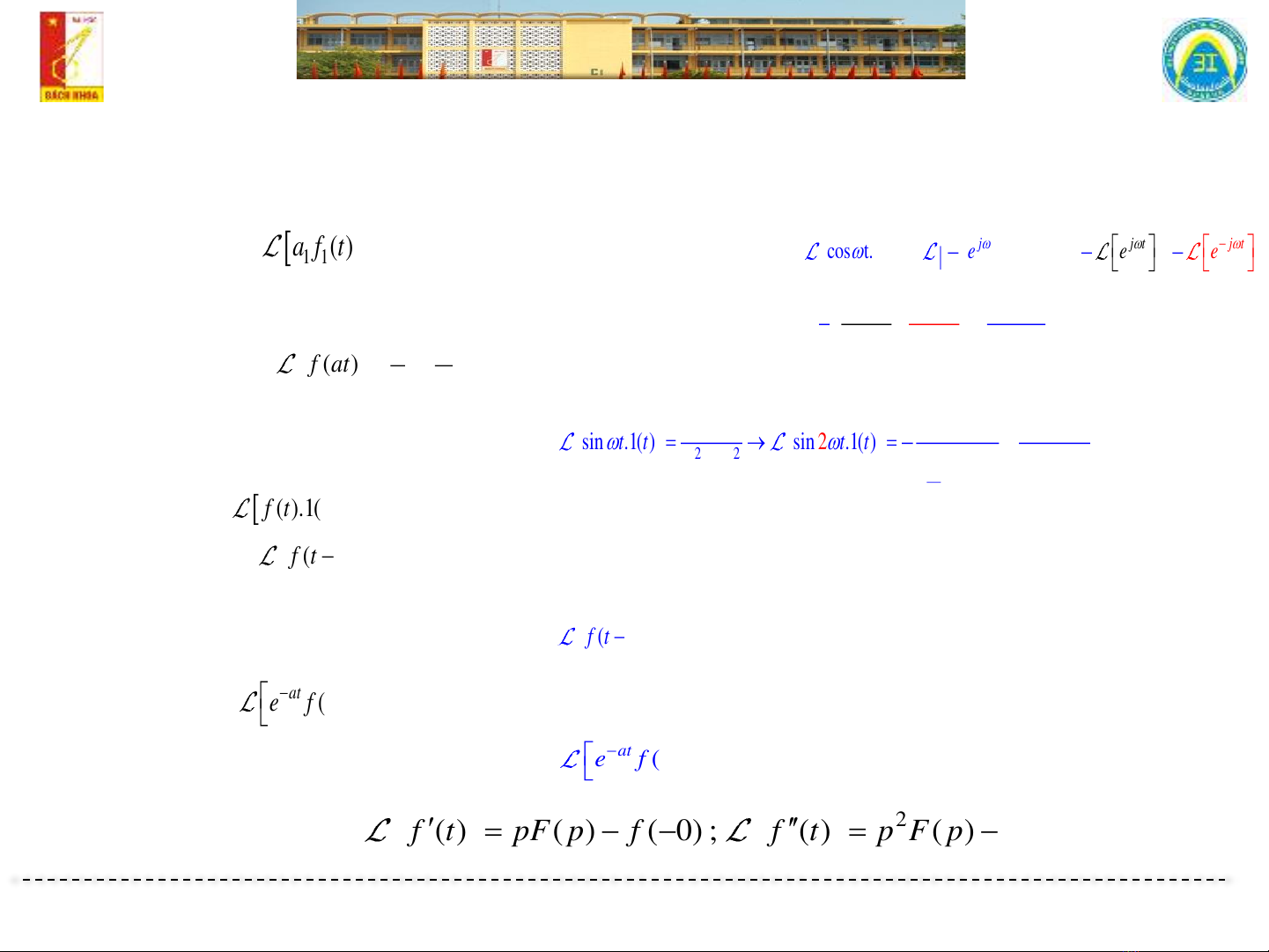
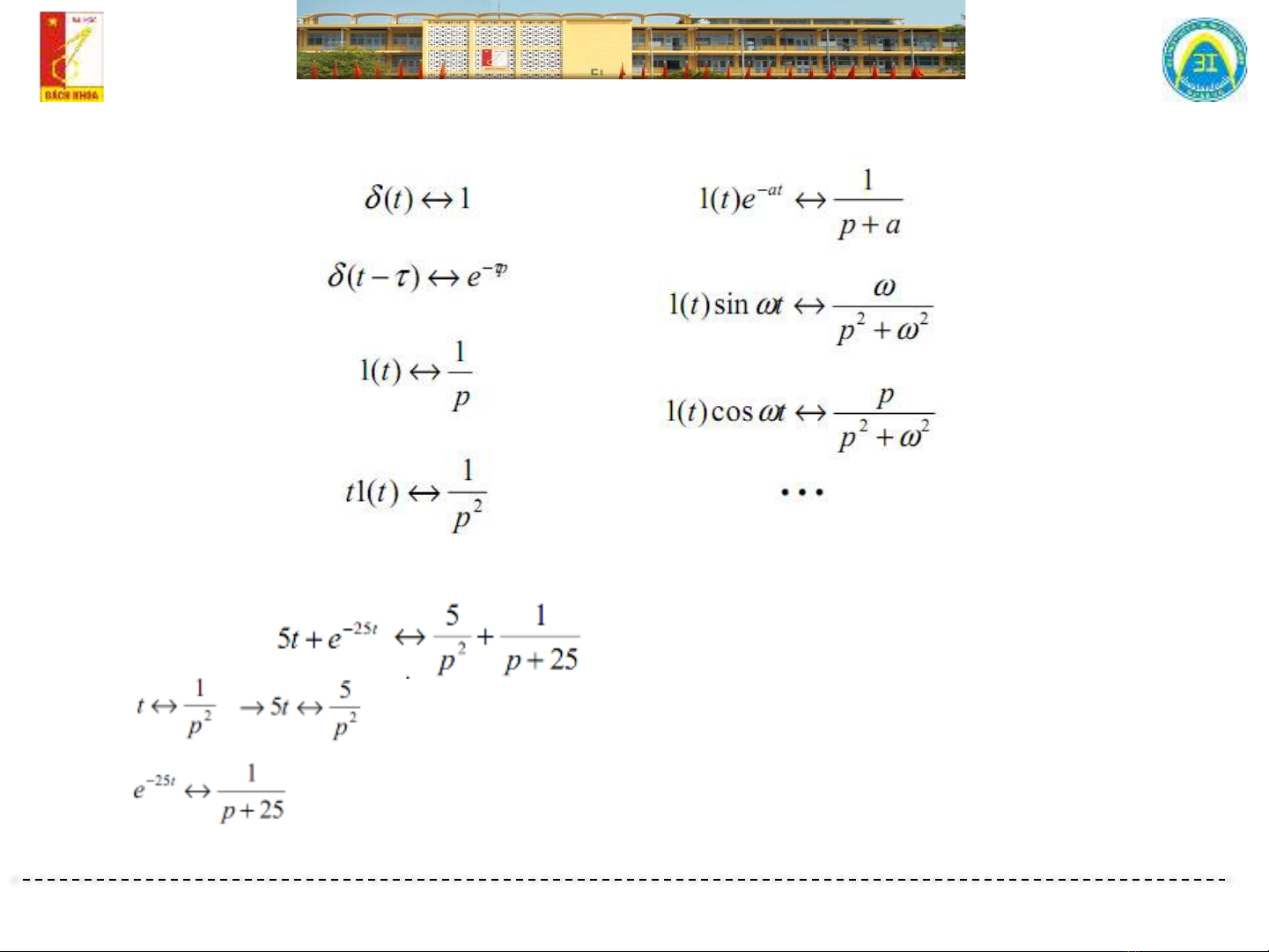
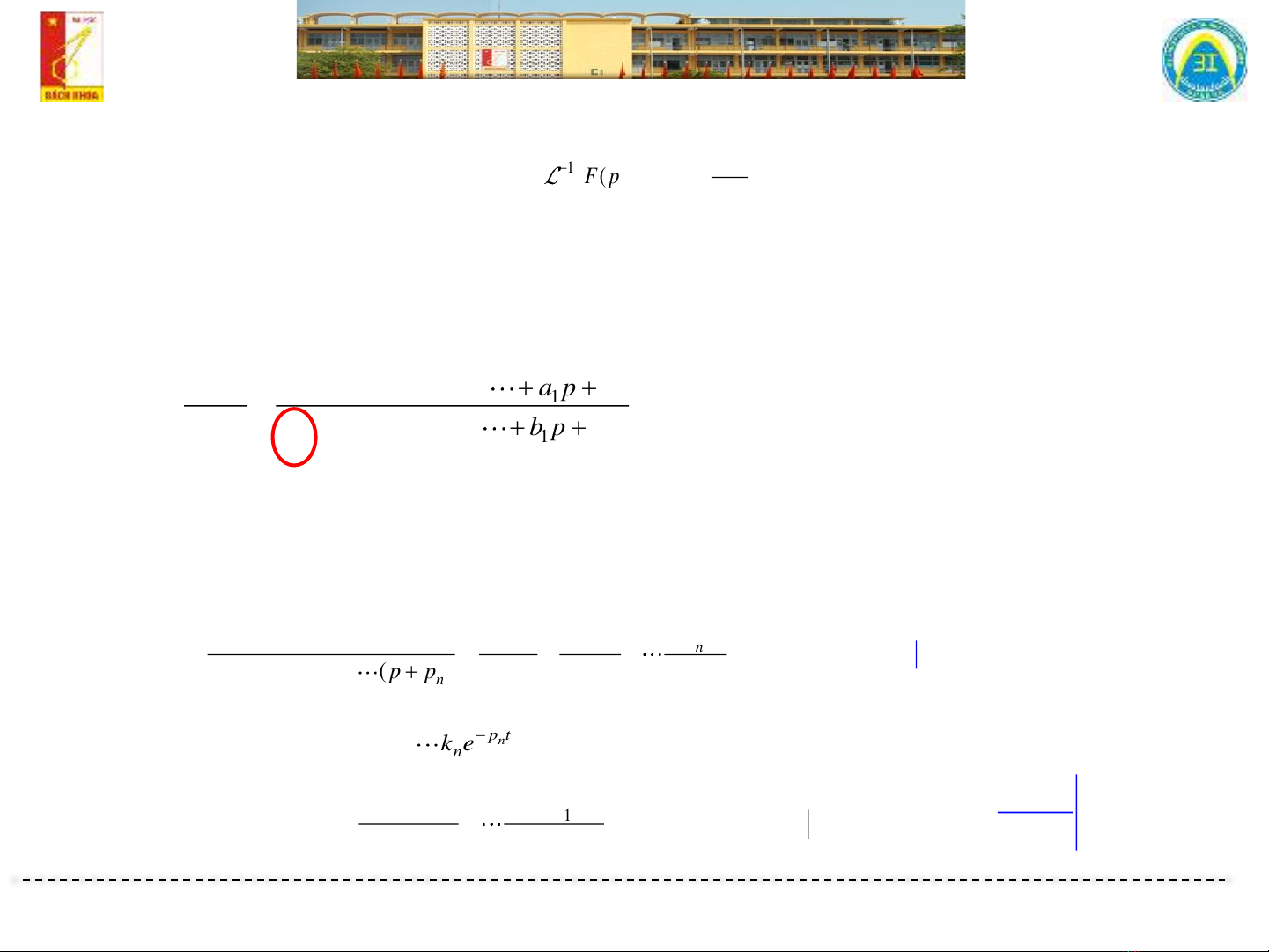
Bài giảng Lý thuyết mạch điện 2: Chương 2.2 - Phương pháp Toán tử Laplace giới thiệu về quy tắc chung của Toán tử Laplace, cách áp dụng nó và các tính chất của nó. Ngoài ra, bài giảng cũng cho biết đến các yếu tố trong hệ thống điện như: kay tính, dòng điện và dòng điện lưu, và cách sử dụng Toán tử Laplace để giải quyết các vấn đề trong lĩnh vực mạch điện. Ngoài ra, bài giảng cũng chia sẻ với học viên các ví dụ để giúp họ hiểu rõ hơn về phương pháp này.