1
➢Phương pháp tích phân kinh điển
▪Lập phương trình đặc trưng và số mũ đặc trưng
▪Xác định các hằng số tích phân
▪Giải mạch bằng phương pháp tích phân kinh điển
➢Phương pháp toán tử Laplace
▪Khái quát
▪Phép biến đổi Laplace và tính chất
▪Tìm gốc từ ảnh Laplace
▪Ứng dụng phép biến đổi Laplace giải mạch điện
Chương 2:
Các phương pháp tính quá trình quá độ
trong mạch điện tuyến tính
2
▪Nghiệm quá độ: xếp chồng nghiệm xác lập và nghiệm tự do:
• Nghiệm xác lập :
Nghiệm xác lập được tìm ở chế độ mới (sau khi đóng,cắt,chuyển
mạch khóa K).
Nghiệm xác lập được nguồn (kích thích) của mạch duy trì. Quy luật
biến thiên của nó đặc trưng cho quy luật biến thiên của nguồn.
Nghiệm xác lập là nghiệm riêng của phương trình vi phân có vế phải
là kích thích của mạch.Ta đã biết cách tính nghiệm xác lập khi kích
thích của mạch là nguồn hằng, nguồn điều hòa, hay nguồn chu kỳ.
Không được nguồn duy trì. Nghiệm tự do tồn tại trong mạch là do quá
trình đóng cắt,chuyển mạch khóa Klàm thay đổi kết cấu hay thông
số của mạch.
Nghiệm tự do là nghiệm riêng của phương trình vi phân thuần nhất
(phương trình vi phân có vế phải bằng 0)
• Nghiệm tự do:
Phương pháp tích phân kinh điển
( ) ( ) ( )
qd xl td
x t x t x t
=+
3
➢Tìm nghiệm xác lập
-Sử dụng các phương pháp giải mạch xác lập tuyến tính
đối với mạch mới bằng các phương pháp đã học
➢Tìm biểu diễn của nghiệm tự do
- Lập phương trình đặc trưng của mạch
-Giải phương trình đặc trưng, biểu diễn dạng nghiệm tự do
➢Biểu diễn dạng nghiệm quá độ=nghiệm xác lập + nghiệm tự do
(còn chứa các hằng số tích phân)
➢Tính sơ kiện. Tính các hằng số tích phân dựa vào sơ kiện tìm được
➢Tìm được nghiệm quá độ
Tích phân kinh điển – Các bước thực hiện
4
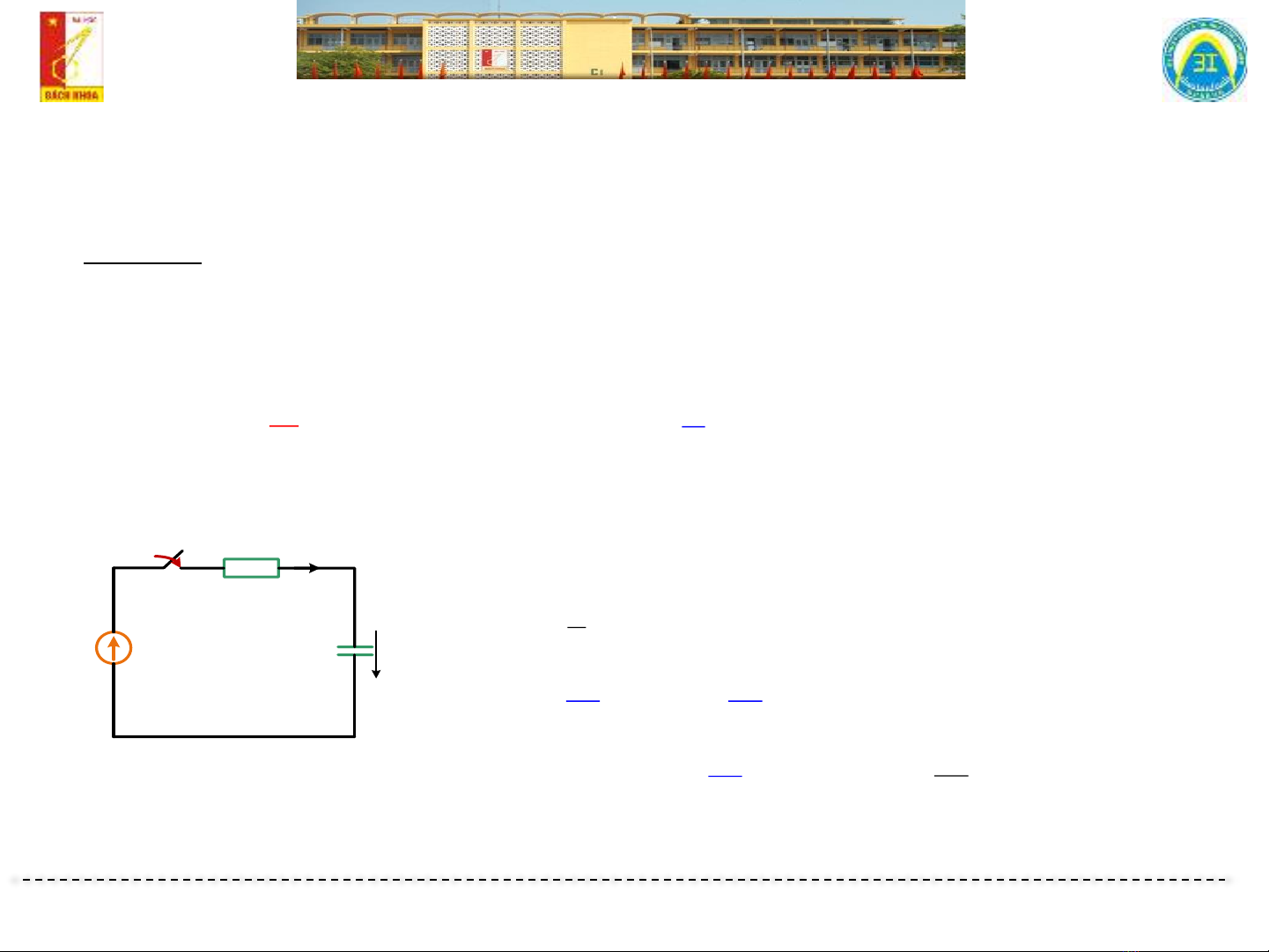
❖Lập phương trình đặc trưng (hai cách)
Cách 1: Đại số hóa phương trình thuần nhất:
-Lập (hệ) phương trình vi tích phân của mạch ở chế độ mới.
-Loại bỏ các nguồn kích thích, thu được phương trình vi phân thuần nhất.
-Thay thế:
Phương trình đặc trưng
( )
()
dp
dt
e
K
R
C
()
C
ut
()it
0
11
0Ri i
pp
Ri
CC

+ = + =


1
( ) ( )dt p
10Ri idt
C
+ =
10RCp
→ + =
1
pRC
−
→=
5
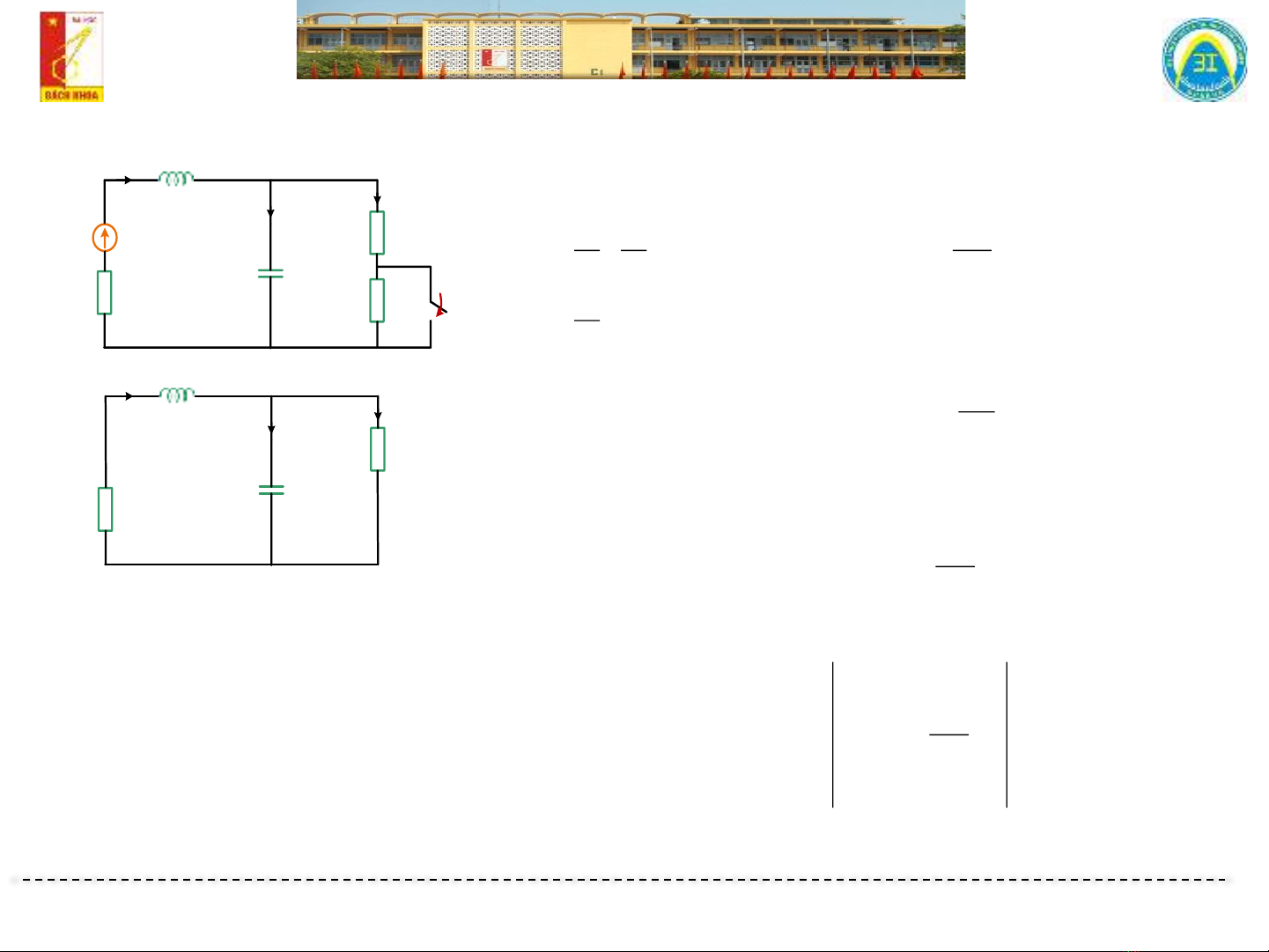
1 2 3
1
1 1 1 2
2
1
1 1 1 3 3
0
0
1
0
i i i
di
R i L i dt
dt C
di
R i L R i
dt
− − =
+ + =
+ + =
E
2
C
K
2
i
1
i
3
R
4
R
1
L
1
R
3
i
E
2
C
2
i
1
i
3
R
1
L
1
R
3
i
1 2 3
1 1 1 1 2
2
1 1 1 1 3 3
0
10
0
i i i
R i L pi i
Cp
R i L pi R i
− − =
+ + =
+ + =
( )
( )
1 2 3
1 1 1 2 3
2
1 1 1 2 3 3
0
100
00
i i i
R L p i i i
Cp
R L p i i R i
− − =
+ + + =
+ + + =
Lập phương trình đặc trưng- cách 1
1
1 1 2
2
3
1 1 3
1 1 1 0
100
0
0
i
R L p i
Cp i
R L p R

−− 

 

→ + =
 

 



+


11
2
1 1 3
1 1 1
100
0
R L p Cp
R L p R
−−
+ =
+
2
3 1 2 1 3 2 1 1 3
( ) ( ) 0R L C p R R C L p R R + + + + =