1
➢Phương pháp tích phân kinh điển
▪Lập phương trình đặc trưng và số mũ đặc trưng
▪Xác định các hằng số tích phân
▪Giải mạch bằng phương pháp tích phân kinh điển
Chương 2:
Các phương pháp tính quá trình quá độ
trong mạch điện tuyến tính
➢Phương pháp toán tử Laplace
▪Khái quát
▪Phép biến đổi Laplace và tính chất
▪Tìm gốc từ ảnh Laplace
▪Ứng dụng phép biến đổi Laplace giải mạch điện
2
❖Biến đổi Laplace
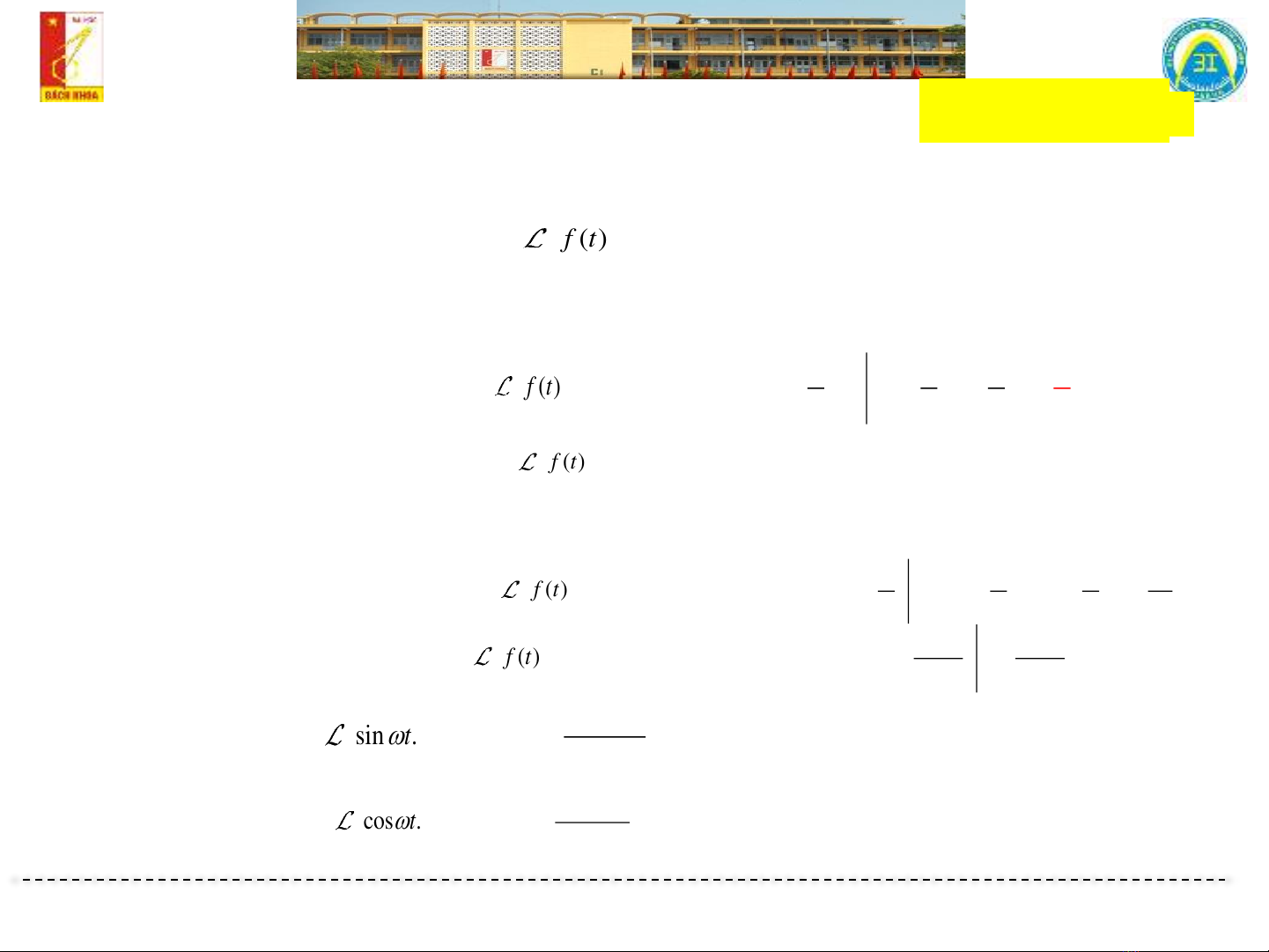
▪Biến đổi Laplace của hàm f(t):
Lưu ý: nhiều tài liệu ký hiệu s thay vì p
▪Một số biến đổi Laplace cơ bản
0
)
((
) ( ) . pt
ft
f t F p e dt
−
−
==
0
0 0 0
00
00
1 1 1
( ) = ( ) ( ) . (0) (1)
pt pt F
f t F const f t F p e dt F e F F
pp
Fpp
−−
−−

= = = = − = − + =


( )
0
00
0
00
1
( ) ( ) ( ) . pa
tt
a pt
atF
f t F e f t F p e dt F e pa
Fpa
e
−−+
−−
−

= = = = − =

++

Phương pháp toán tử Laplace
0
0
( ) ( ) ( ) ( ) .
( ) 1
pt
f t t f t F p te dt e
−−
−
= = = = =
•Hàm đơn vị 1(t):
•Hàm Dirac (t):
0
0
1 1 1
( ) 1( ) ( ) ( ) . 1
1( (0) (1)
)pt pt
f t t f t F p e dt
te
p p p p
−−
−
= = = = − = − + =
•Một số hàm khác:
22
cos .1( ) ( ) p
t t F p p
==
+
22
sin .1( ) ( )t t F p p
==
+
p
Toán tử Laplace:
3
Biến đổi Laplace
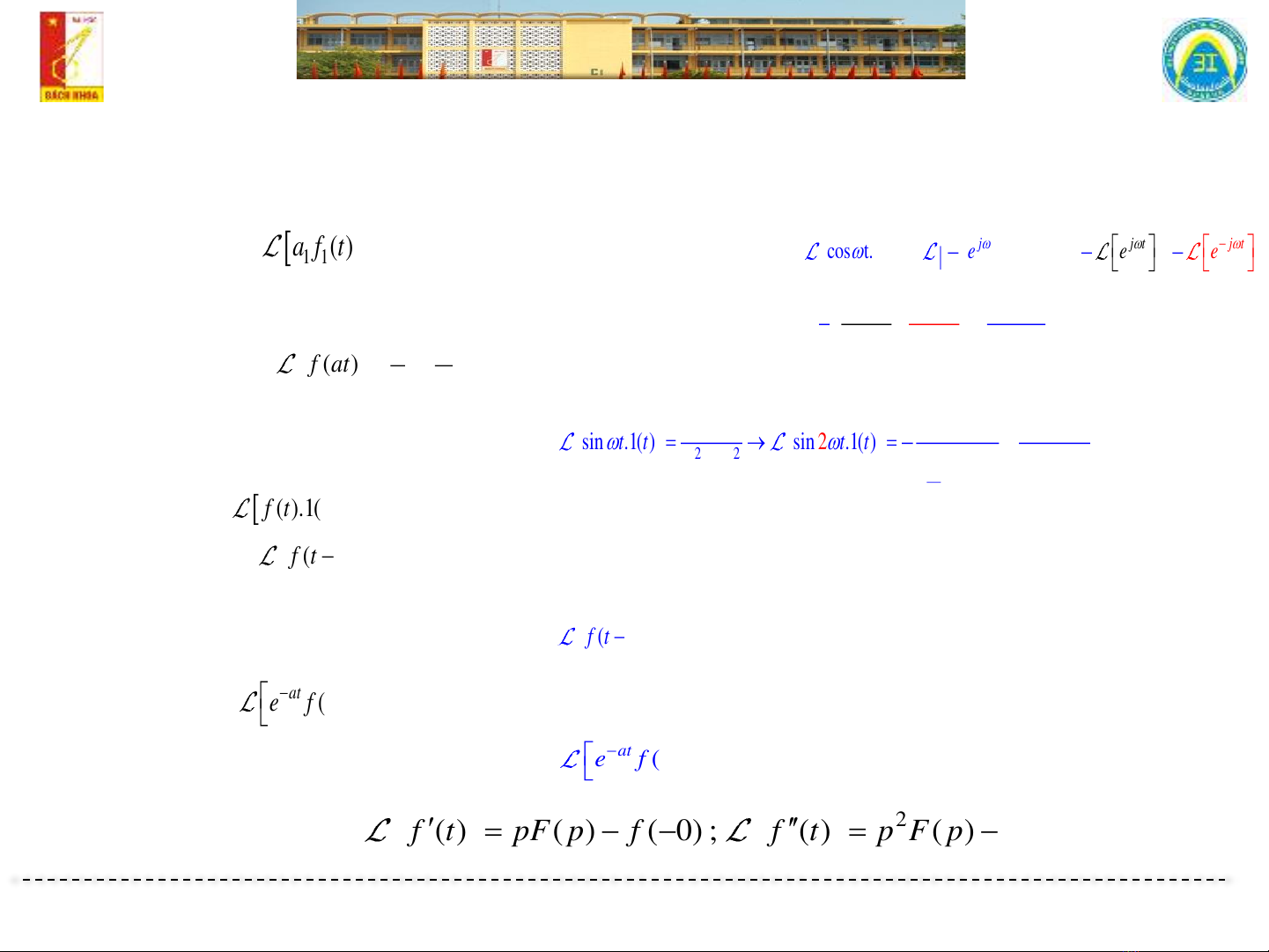
▪Tuyến tính Ví dụ:
▪Đồng dạng:Ví dụ:
▪Tính trễ:
( ).1( ) ( )
( ).1( ) ( )
-ap
f t t F p
f t a t a e F p
=
− − =
()
00
( ).1( ) ( ) ( ) ( ) ( )
pt p x a ap px ap
a
f t a t f t a e dt f x e dx e f x e dx e F p
− − + − − −
−−
− = − = = =
▪Dịch ảnh:
( ).1( ) ( )
at
e f t t F p a
−
=+
()
00
( ).1( ) ( ) ( ) ( )
at at pt p a t
e f t t e f t e dt f t e dt F p a

− − − − +
= = = +

▪Ảnh đạo hàm gốc:
❖Tính chất của biến đổi Laplace
Chứng minh: đặt: x=t-a →dx=dt, t=x+a
1 1 2 2 1 1 2 2
( ) ( ) ( ) ( )a f t a f t a F p a F p+ = +
( )
22
1 1 1
cos t.1(t) 2 2 2
111
2
j t j t jttj
e
pj
pj
eee
p
p
−−


= + = +

−



= + =

++

1
( ) ( )
p
f at F
aa
=
2
( ) ( ) ( 0) ; ( ) ( ) ( 0) ( 0)f t pF p f f t p F p pf f
= − − = − − − −
Chứng minh:
4
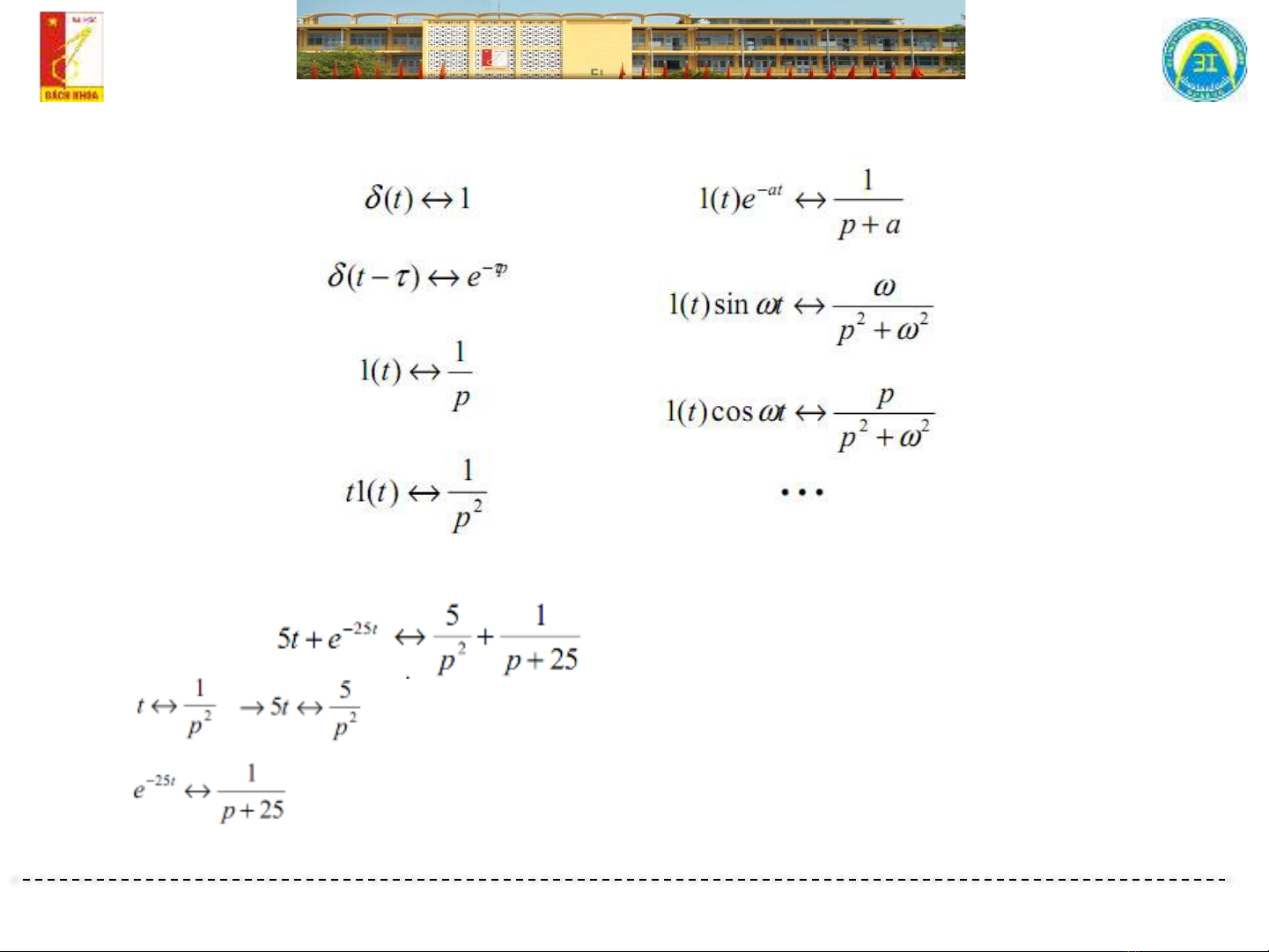
Bảng biến đổi Laplace
▪Ví dụ
5
Biến đổi ngược Laplace (1)
11
( ) ( ) ( ) ( )
2
jpt
j
F p F p f t F p e dt
j


+
−
−
= =
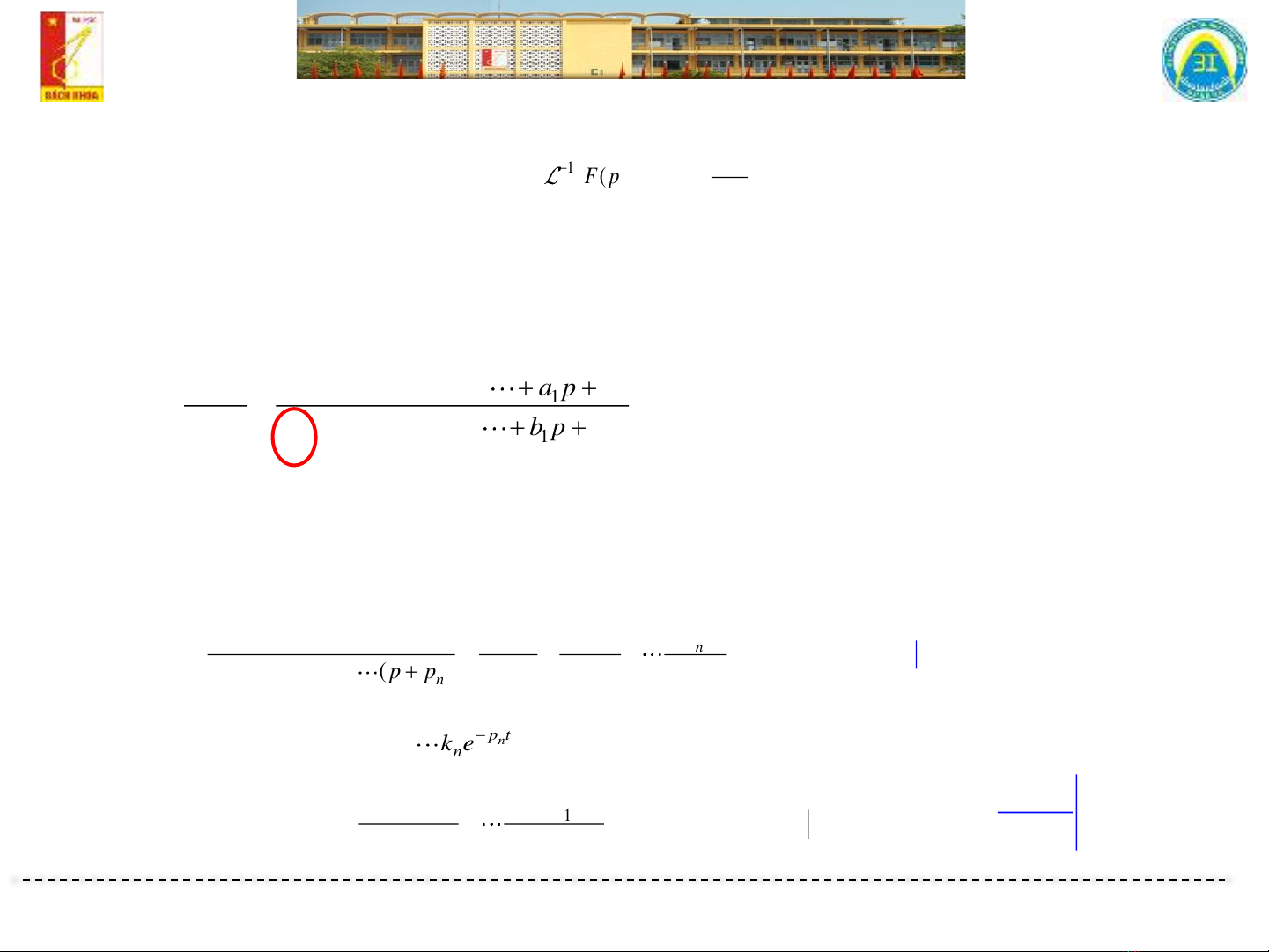
❖Biến đổi ngược Laplace
▪Tìm gốc thời gian từ ảnh Laplace: Dùng bảng ảnh-gốc hoặc theo phương
pháp Heaviside:
Thực tế ít dùng công thức này (yêu cầu hội tụ,…).
1
1 1 0
1
1 1 0
()
() ()
mm
mm
nn
nn
a p a p a p a
Np
Fp Dp b p b p b p b
−
−−
−
+ + + +
==+ + + +
Lưu ý: chỉ xét cho phân thức hữu tỉ
này khi m
n
Với m
n, cần chia đa thức để được
dạng trên.
Đưa về dạng bn=1 để tiện tính toán
•Tìm nghiệm của đa thức mẫu số:
( ) 0 i
D p p
=
➢Nếu pilà các nghiệm đơn, riêng biệt:
12
12
() n
pt
p t p t
n
f t k e k e k e−
−−
= +
12
1 2 1 2
()
( ) ;
( )( ) ()
()(
)i
ii
p
n
nn
p
k
N p k k
Fp p p p p p p p p p p p p k p p F p =−
= = + +
+ + + + + =+
+
Ví dụ:
()
() i
i
pp
Np
kDp =−
=
Có thể tính theo công thức:
1
1
12
1 1 1 1
2
()
()
( ) ( ) ( ) ( )
n
pp
n
p p k
p p k
p p F p k k p p F p
p p p p =−
+
+
+ = + + → = +
++