1
https://sites.google.com/site/thaott3i/
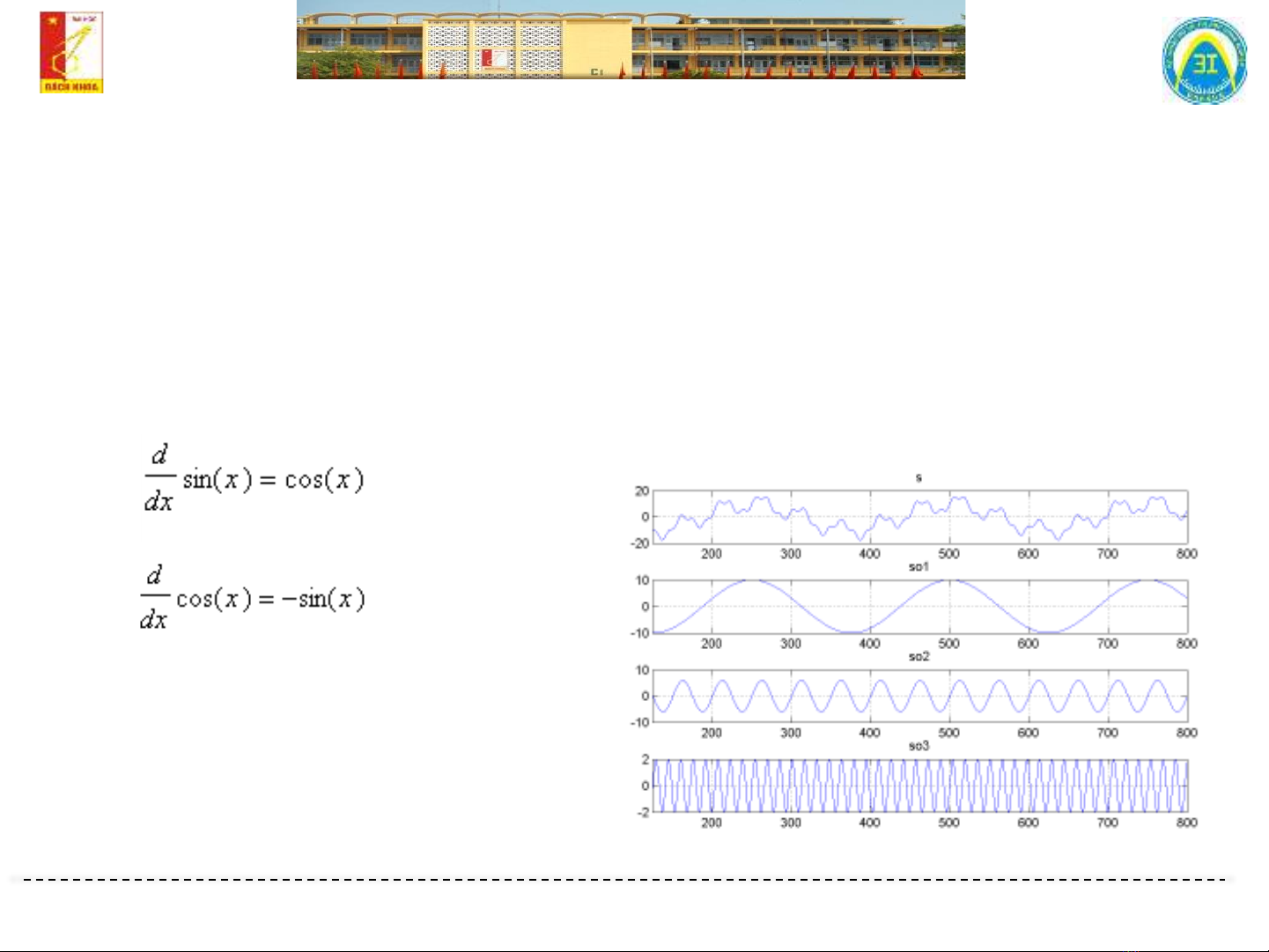
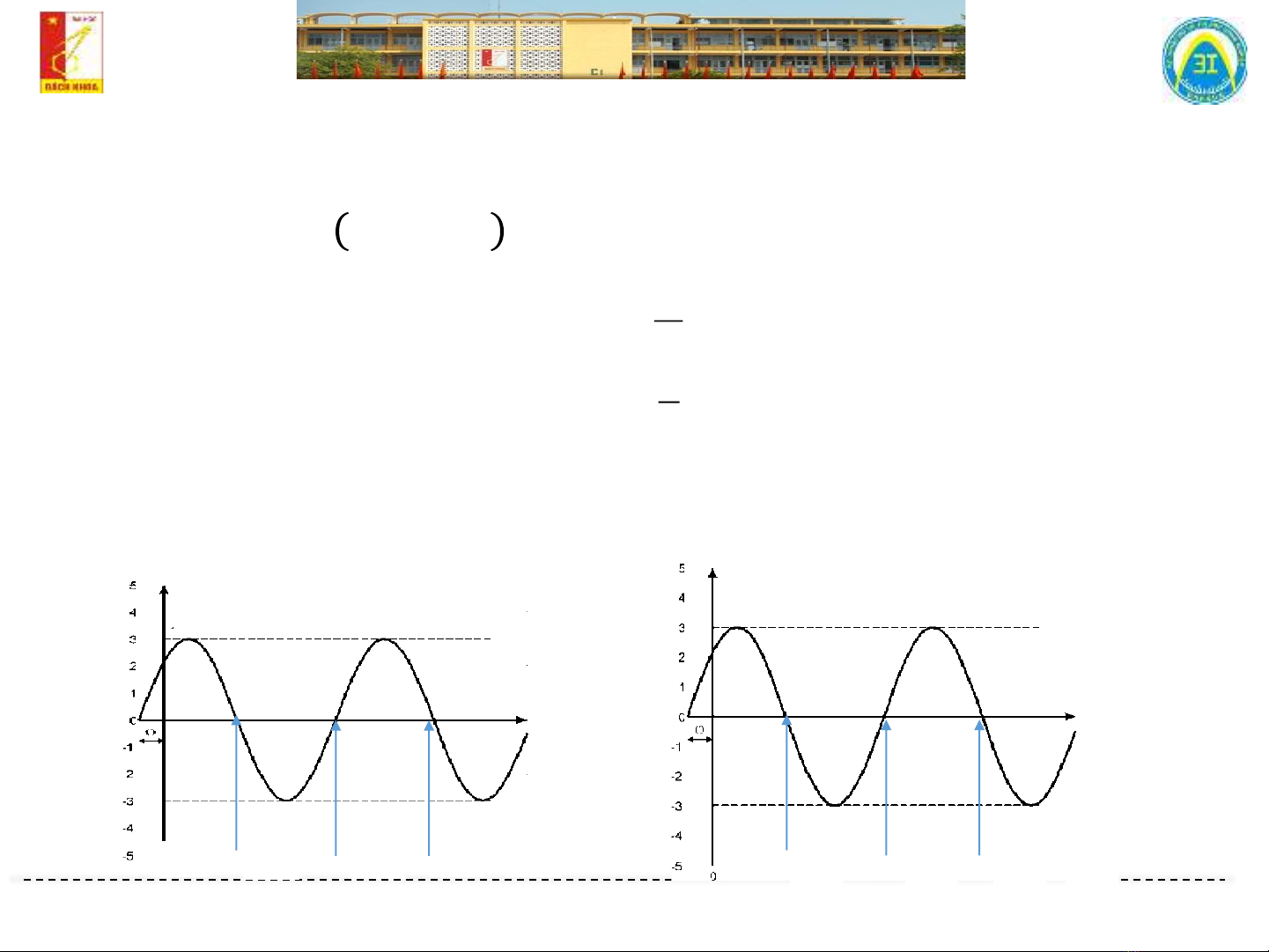
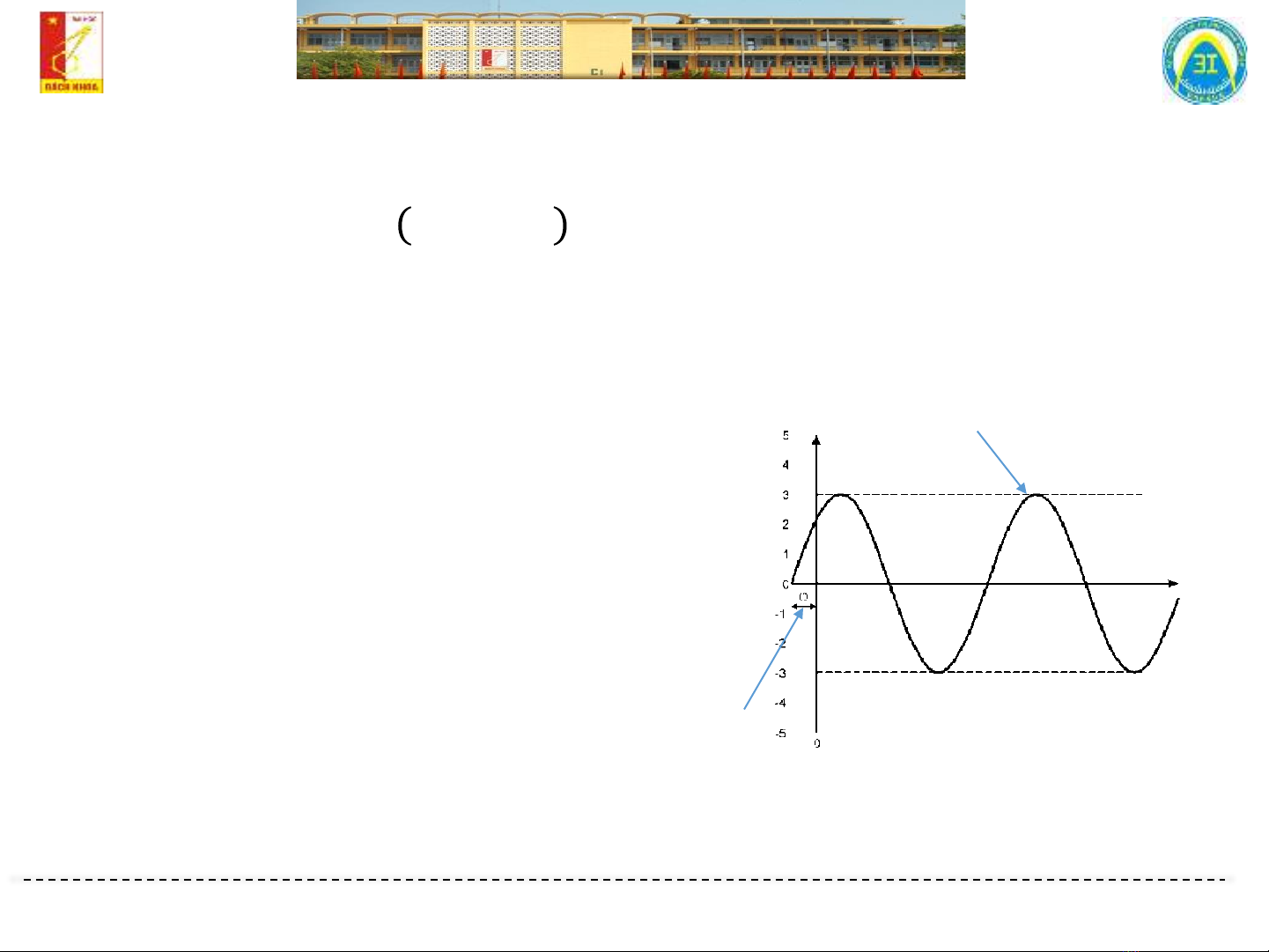
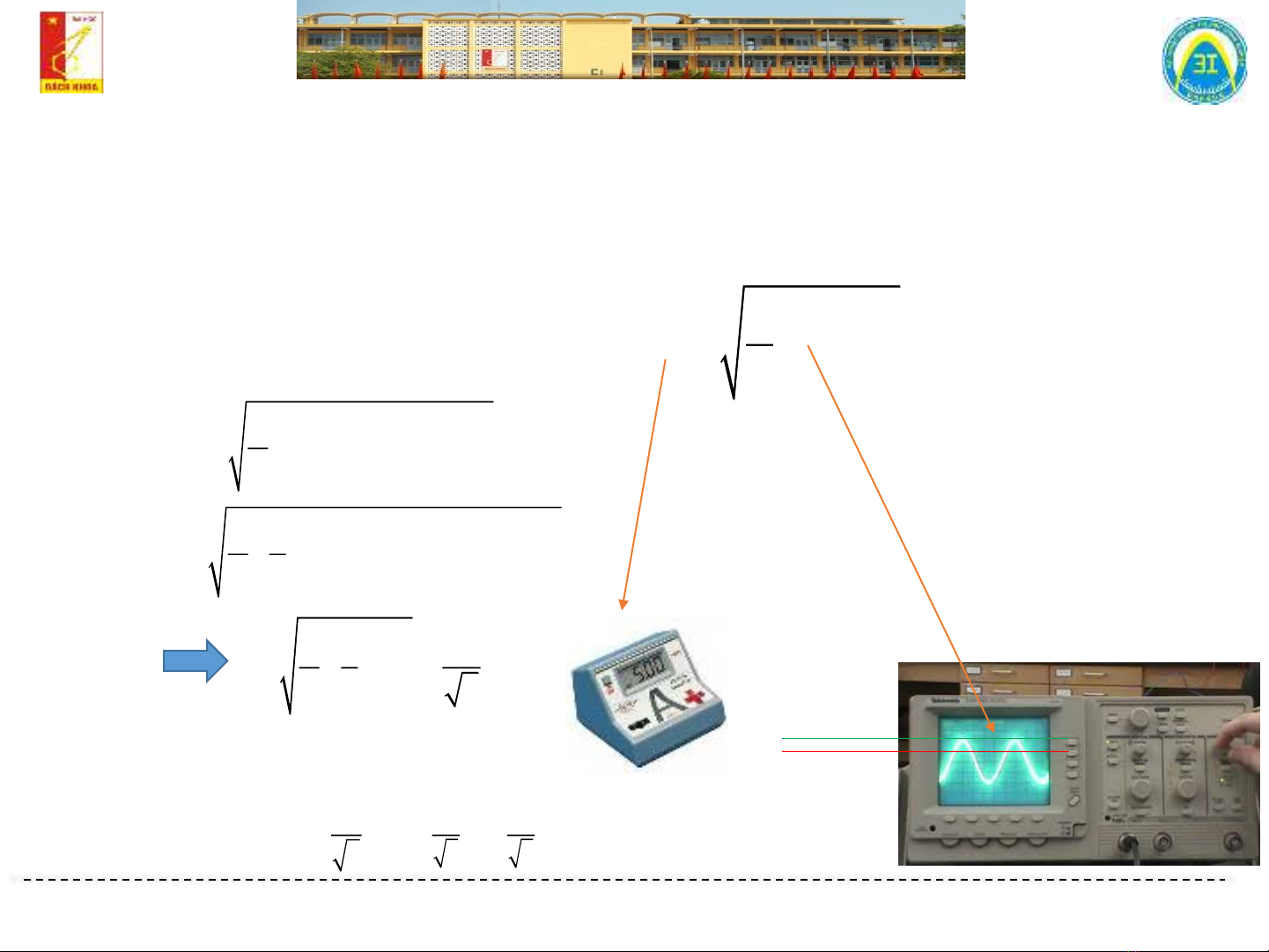
➢Mạch xoay chiều hình sin
▪Quan hệ dòng-áp trên các phần tử R,L,C
▪Biểu diễn dạng phức
▪Sơ đồ phức của mạch điện
➢Định luật Kirchhoff dạng phức
▪Định luật Kirchhoff về dòng điện
▪Định luật Kirchhoff về điện áp
▪Hệ phương trình Kirchhoff độc lập
➢Công suất
Chương 3:
Mạch tuyến tính ở chế độ xác lập hình sin
2
https://sites.google.com/site/thaott3i/
❖Ý nghĩa nghiên cứu chế độ xác lập hình sin:
▪Thực tế: Hầu hết các thiết bị sử dụng trong hộ gia đình, nhà
máy đều làm việc với nguồn hình sin
▪Hàm sin là một hàm cơ bản
• Tín hiệu bất kỳ có thể phân tích thành
tổng các hàm hình sin: Fourier
• Tiện tính đạo hàm, tích phân,…
Chế độ xác lập ở mạch điều hòa hình sin
s=so1+so2+so3+…
3
https://sites.google.com/site/thaott3i/
❖Hàm điều hòa hình sin
𝑖(𝑡) = 𝐼𝑚sin 𝜔𝑡 + 𝜑𝑖
Im: biên độ dòng điện
: tần số góc (rad/s)
(ωt+φi): góc pha (rad)
φi: góc pha đầu (t=0), (độ)
1
Tf
=
: chu kỳ (giây, s)
▪Biểu diễn theo góc pha và thời gian
2
f
=
: tần số (Hertz, Hz)
2f

=
Với f=50Hz (tần số lưới điện)
→=314 rad/s
Hàm điều hòa và các đại lượng đặc trưng (1)
i(t)
Im
-Im
t
T/2 T 3T/2
i(t)
-Im
t3
2
0
Im
4
https://sites.google.com/site/thaott3i/
❖Đặc trưng của dòng hình sin
Đặc trưng bởi cặp thông số (Im,ωt+φi).
Với dòng điện hình sin có cùng tần số,
cặp thông số đặc trưng là:Im,φi
Hàm điều hòa và các đại lượng đặc trưng (2)
𝑖(𝑡) = 𝐼𝑚sin 𝜔𝑡 + 𝜑𝑖
i(t)
Im
-Im
t
T/2 T 3T/2
5
https://sites.google.com/site/thaott3i/
▪Dòng điện hiệu dụng
2
0
11
22
T
m
m
I
I I dt
T
==
Trị hiệu dụng Ilà trị trung bình bình phương của hàm chu kỳ i(t)
2
0
1()
T
I i t dt
T
=
( )
( )
22
0
2
0
1sin
11 1 cos2
2
T
mi
T
mi
I I t dt
T
I t dt
T


=+

= − +

Tương tự, với u(t) , e(t), j(t)
;
2
m
U
U=
;
2
m
E
E=
Hàm điều hòa và các đại lượng đặc trưng (3)
I
Im