Giới thiệu tài liệu
Tài liệu này cung cấp một cái nhìn tổng quan về động học và động lực học của quá trình quay vòng ô tô, một chủ đề quan trọng trong kỹ thuật ô tô. Nó bao gồm các khái niệm cơ bản, các yếu tố ảnh hưởng đến khả năng quay vòng của xe, và các phương pháp phân tích và thiết kế hệ thống lái.
Đối tượng sử dụng
Sinh viên và kỹ sư ngành kỹ thuật ô tô, những người quan tâm đến việc tìm hiểu sâu hơn về động học và động lực học của quá trình quay vòng ô tô và thiết kế hệ thống lái.
Nội dung tóm tắt
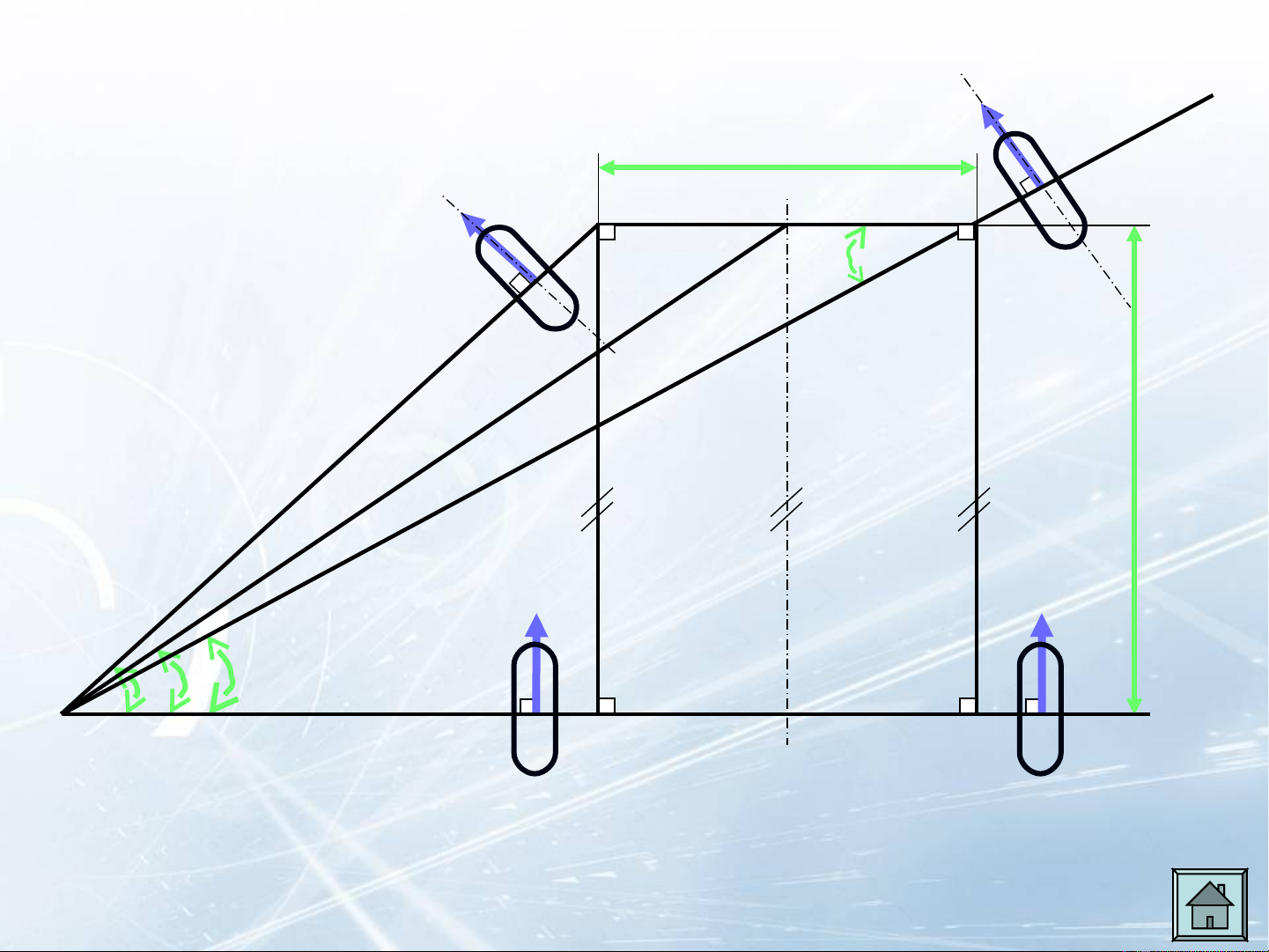
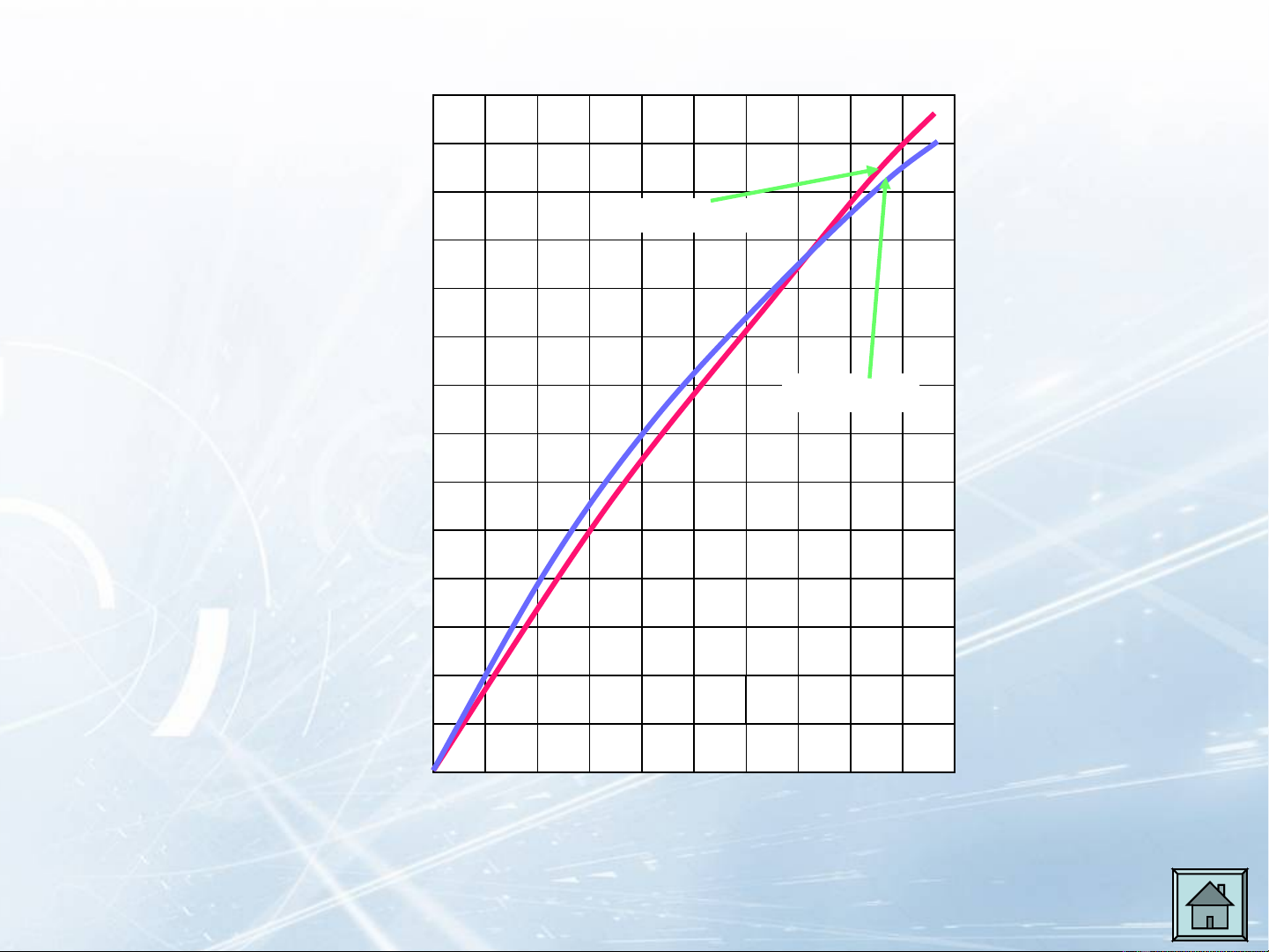
Tài liệu này trình bày chi tiết về động học và động lực học quay vòng của ô tô, bắt đầu bằng việc thiết lập các phương trình toán học mô tả mối quan hệ giữa các góc quay của bánh xe và bán kính quay vòng. Các yếu tố ảnh hưởng đến tính chất quay vòng của xe, bao gồm độ cứng của lốp và hình học hệ thống treo, được phân tích kỹ lưỡng. Tài liệu cũng đi sâu vào thiết kế và phân tích hình thang lái, một thành phần quan trọng của hệ thống lái, đảm bảo rằng các bánh xe dẫn hướng quay theo một quan hệ nhất định để tránh trượt. Các loại cơ cấu lái khác nhau và truyền động lái cũng được mô tả, cùng với các ưu điểm và nhược điểm của chúng. Cuối cùng, tài liệu xem xét các lực tác dụng lên hệ thống lái và cách chúng ảnh hưởng đến nỗ lực lái xe cần thiết.

























![Bài giảng Kỹ thuật điện - điện tử ô tô [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260121/hoatrami2026/135x160/37681769069450.jpg)



