Bài giảng Mô hình hồi quy tuyến tính đơn giản

Chia sẻ: Menh Menh | Ngày: | Loại File: PDF | Số trang:37

Thêm vào BST

Báo xấu

57
lượt xem 2
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng trình bày phân tích tương quan; mô hình hồi quy tuyến tính đơn giản; kiểm tra giả định mô hình hồi quy tuyến tính. Mời các bạn cùng tham khảo bài giảng để nắm chắc kiến thức.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Mô hình hồi quy tuyến tính đơn giản

Tuan V. Nguyen Senior Principal Research Fellow, Garvan Institute of Medical Research Professor, UNSW School of Public Health and Community Medicine Professor of Predictive Medicine, University of Technology Sydney Adj. Professor of Epidemiology and Biostatistics, School of Medicine Sydney, University of Notre Dame Australia Phân tích dữ liệu và ứng dụng | Đại học Dược Hà Nội | 12/6 to 17/6/2019 © Tuan V. Nguyen
Mô hình hồi qui tuyến tính • Phân tích tương quan • Mô hình hồi qui tuyến tính đơn giản • Kiểm tra giả định mô hình hồi qui tuyến tính
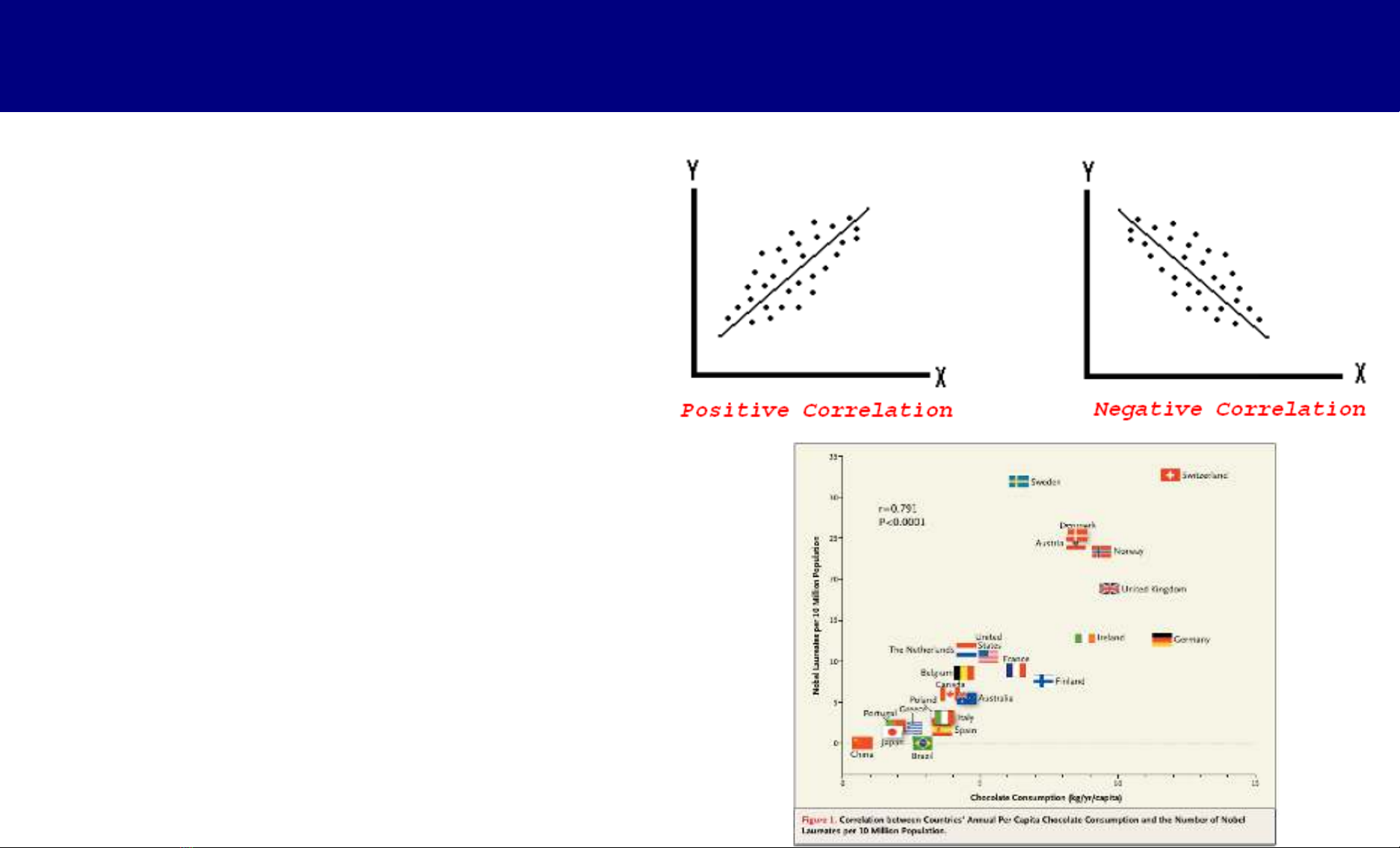
Khái niệm tương quan (correlation) • Khi hai biến số (x và y) có liên quan với nhau • Mối liên quan có thể cùng chiều hay nghịch đảo • Ví dụ: mối liên quan giữa tiêu thụ chocolate và giải Nobel (?)
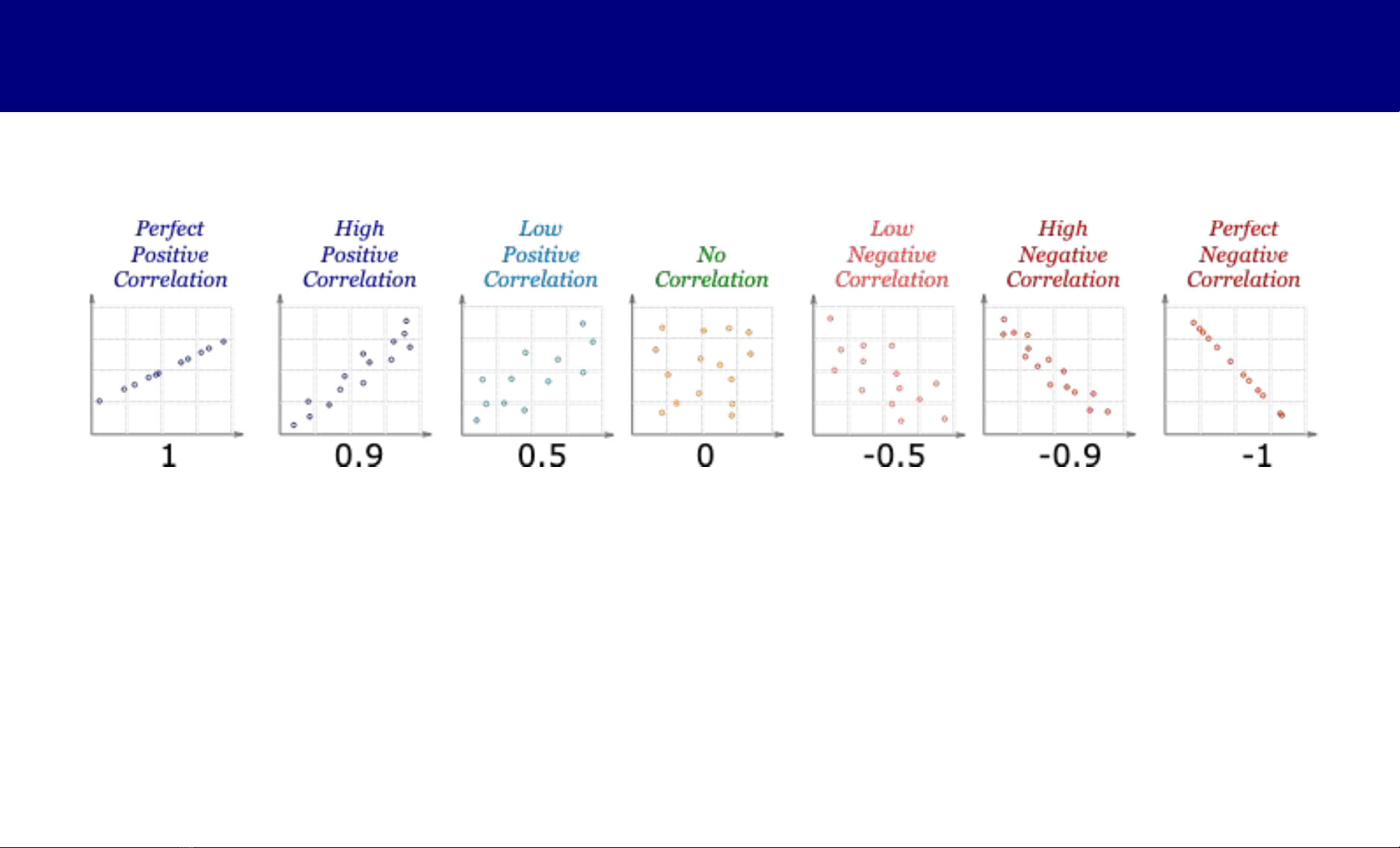
Tương quan giữa 2 biến liên tục Làm sao định lượng mối liên quan?
Sir Francis Galton (16/2/1822 – 17/1/1911) Research interest: Didn’t have data on “intelligence” so instead studied HEIGHT “Those qualifications of intellect and disposition which … lead to reputation” Galton’s conclusions: • Nature dominates: “families of reputation were much more likely than ordinary families to produce offspring of ability” • Recommended “judicious marriages during several generations” to “produce a highly gifted race of men” • His “genetic utopia”: “Bright, healthy • Although a self-proclaimed genius, who wrote that he individuals were treated and paid well, and could read @2½, write/do arithmetic @4, and was encouraged to have plenty of children. Social comfortable with Latin texts @8, he couldn’t figure undesirables were treated with reasonable out how to model these data(!) kindness so long as they worked hard and stayed celibate.” • He went to JD Dickson, a mathematician at Cambridge, who formalized the relationship by J Singer's slide developing what we now know as linear regression
Làm thế nào để mô tả mối tương quan tuyến tính? • Gọi X và Y là 2 biến ngẫu nhiên từ n quan sát • Đo lường độ biến thiên: phương sai (variance) var( x ) = å ( xi - x )2 ( yi - y )2 var( y ) = å n n i =1 n -1 i =1 n -1 • Chúng ta cần một thước đo độ "hiệp biến" giữa X và Y • Covariance là trung bình của tích số X và Y 1 n cov( x, y ) = å ( xi - x )( yi - y ) n - 1 i =1
Ước tính hệ số tương quan • Covariance có đơn vị đo lường (X * Y). • Coefficient of correlation (r) giữa X và Y là một standardized covariance – không có đơn vị đo lường • r định nghĩa như sau: cov( x, y ) cov( x, y ) r= = var( x ) ´ var( y ) SDx ´ SDy
Obesity data (Vietnam) • Nghiên cứu cắt ngang >1100 nam và nữ (Việt Nam) • Mục tiêu: ước tính hệ số tương quan giữa tỉ trọng cơ thể (bmi) và tỉ trọng mỡ (pcfat) ob = read.csv("~/Dropbox/_Conferences and Workshops/Dai hoc Duoc 6- 2019/Datasets/obesity data.csv") dim(ob) [1] 1217 11 > head(ob) id gender height weight bmi age bmc bmd fat lean pcfat 1 1 F 150 49 21.8 53 1312 0.88 17802 28600 37.3 2 2 M 165 52 19.1 65 1309 0.84 8381 40229 16.8 3 3 F 157 57 23.1 64 1230 0.84 19221 36057 34.0 4 4 F 156 53 21.8 56 1171 0.80 17472 33094 33.8 5 5 M 160 51 19.9 54 1681 0.98 7336 40621 14.8 6 6 F 153 47 20.1 52 1358 0.91 14904 30068 32.2
Hàm cor.test > cor.test(ob$bmi, ob$pcfat) data: ob$bmi and ob$pcfat t = 17.123, df = 1215, p-value < 2.2e-16 alternative hypothesis: true correlation is not equal to 0 95 percent confidence interval: 0.3944998 0.4850923 sample estimates: cor 0.4409183
Phân tích tương quan đa biến (GGally) • Hàm cor.test chỉ tính toán tương quan giữa 2 biến • Với k biến, chúng ta có k(k – 1)/2 hệ số tương quan • Mục tiêu: tính toán tất cả mối tương quan • Package "GGally" library("GGally") ggcorr(dat, label=T)
Phân tích tương quan đa biến Dữ liệu: tất cả biến số phải là biến liên tục # Mục tiêu: tính hệ số tương quan cho nhiều biến trong ob # loại trừ 2 cột đầu tiên của ob, chỉ quan tâm đến các biến liên tục dat = ob[, -c(1,2)] # loại bỏ 2 biến số 1 và 2 (id, gender) library("GGally") ggcorr(dat, label=T)
dat = ob[, -c(1,2)] # loại bỏ 2 biến số 1 và 2 (id, gender) library("GGally") ggcorr(dat, label=T) pcfat lean -0.4 fat 0.1 0.8 bmd -0.1 0.4 -0.3 1.0 0.5 bmc 0.9 0 0.7 -0.4 0.0 -0.5 age -0.5 -0.4 0.2 -0.2 0.3 -1.0 bmi 0.2 0.2 0.1 0.8 0.5 0.4 weight 0.8 0 0.6 0.3 0.6 0.8 0.1 height 0.6 0 -0.4 0.7 0.4 -0.1 0.8 -0.5
ggpairs(dat)
Hàm pairs.panels trong psych dat = ob[, -c(1,2)] # Gọi package psych và dùng hàm pairs.panels library(psych) pairs.panels(dat)
r và R2 • r là hệ số tương quan • R2 là hệ số xác định (coefficient of determination) phản ảnh phần trăm phương sai của y có thể giải thích bởi biến x • r(weight, BMD) = 0.33 có nghĩa là R2 = (0.33)2 = 0.11. 11% độ khác biệt về BMD có thể giải thích bằng những khác biệt về cân nặng
Ý tưởng và nhu cầu mô hình hồi qui tuyến tính 60 2 50 0 40 Y Y -2 30 -4 20 2 4 6 8 10 12 14 16 2 4 6 8 10 12 14 16 X X Làm cách nào để định lượng hóa mối liên quan giữa Y và X ?
Ý tưởng mô hình hồi qui tuyến tính • Biến phụ thuộc (Y) phải là biến liên tục (vd: pcfat) • Biến tiên lượng (X) hay predictor variables: không giới hạn (vd: giới tính, tuổi) • Hồi qui tuyến tính đơn giản (simple linear regression model) – có một biến tiên lượng
Mô hình hồi qui tuyến tính Mô hình: Y = a + bX + e a : intercept b : slope / gradient ε : sai số ngẫu nhiên (random error – những dao động về Y trong mỗi giá trị X)