2
NỘI DUNG
1.Vấn đề thực tiễn dẫn đến bài toán quy
hoạch tuyến tính (QHTT) – Thiết lập mô hình
bài toán
2.Các dạng của bài toán QHTT
3.Phương pháp đồ thị
4.Phương pháp đơn hình
5.Phương pháp đơn hình mở rộng
6.Sử dụng Excel giải bài toán QHTT
3
1.THIẾT LẬP MÔ HÌNH BÀI
TOÁN
Ví dụ 1: (Bài toán lập kế hoạch sản xuất)
Một xí nghiệp có thể sản xuất ra một loại sản phẩm theo 3
phương pháp khác nhau, kí hiệu PP1, PP2, PP3. Các loại
nguyên liệu để sản xuất, kí hiệu N1, N2, N3. Biết rằng số
nguyên liệu để sản xuất hiện có, định mức tiêu hao các loại
nguyên liệu và số lượng sản phẩm sản xuất ra trong một giờ
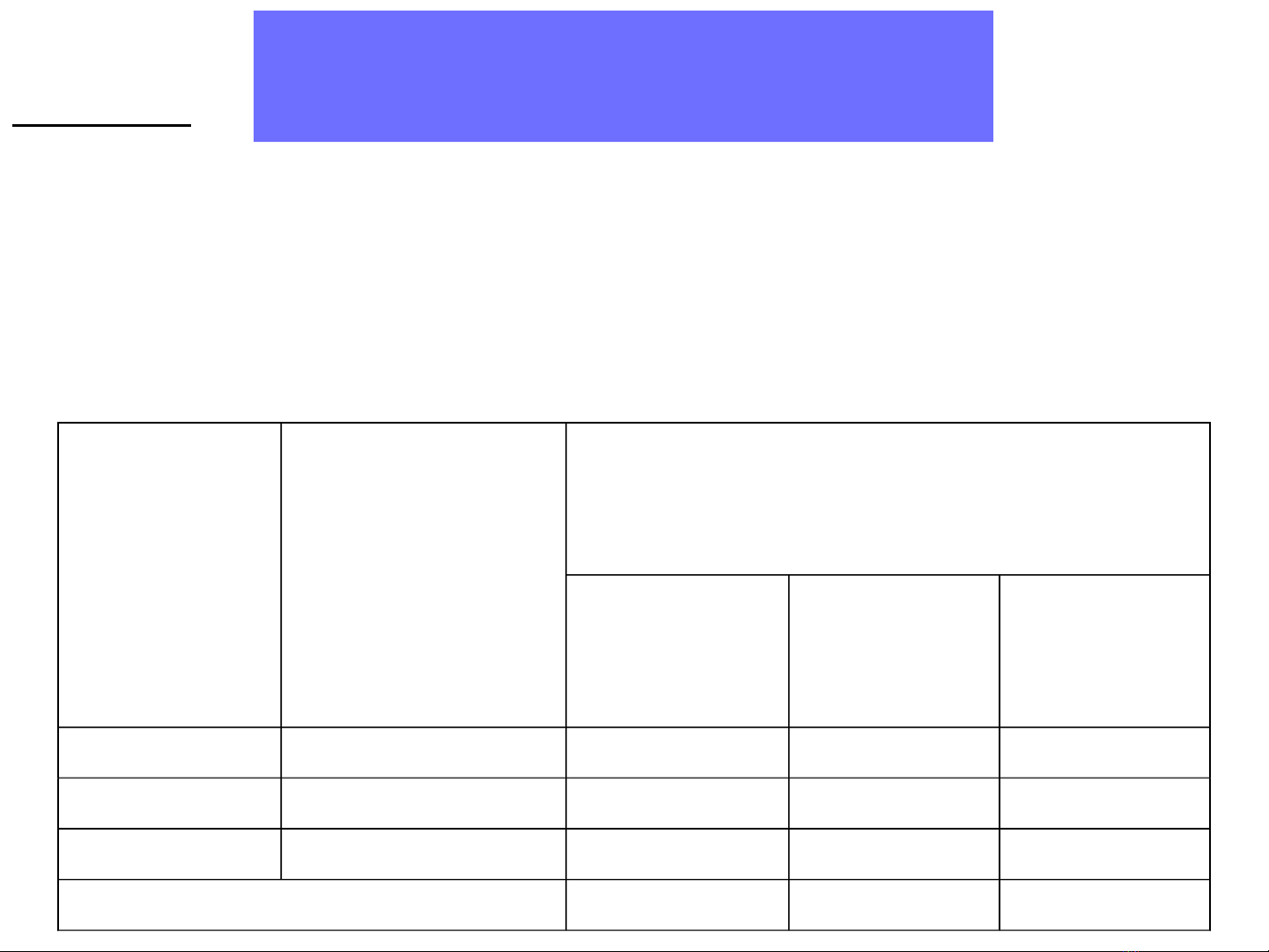
theo các phương pháp cho ở bảng sau:
Nguyên
Liệu
Số lượng
hiện có
(đơn vị)
Định mức tiêu hao trong một
giờ
PP1 PP2 PP3
N1 250 4 5 3
N2 350 2 4 1
N3 450 3 6 4
Sản lượng (đơn vị/giờ) 10 12 9
Hãy lập mô hình bài toán tìm kế hoạch sản xuất sao cho xí
nghiệp sản xuất được nhiều sản phẩm nhất.
4
Cách lập mô hình bài toán:
Bước 1: Đặt ẩn và điều kiện cho ẩn (ràng buộc dấu).
Căn cứ vào yêu cầu của bài toán, xác định số ẩn, đơn vị tính
và điều kiện cho ẩn.
Bước 2: Lập hàm mục tiêu f(x).
Căn cứ vào các ẩn đã đặt, xác định hàm mục tiêu “yêu cầu
tối ưu”.
Bước 3: Lập các ràng buộc.
Căn cứ vào các ẩn đã đặt, xác định các ràng buộc “yêu cầu
kỹ thuật”.
Bước 4: Viết mô hình bài toán.
Sau khi phân tích, ta lập mô hình bài toán dưới dạng sau:
-Hàm mục tiêu.
-Các ràng buộc.
-Các điều kiện.
5
Ví dụ 2: (Bài toán xác định khẩu phần thức ăn)
Để sinh sống trong một ngày đêm, mỗi người cần ít nhất 70g
Protit, 30g Lipit và 420g Gluxit. Hàm lượng các chất trên có
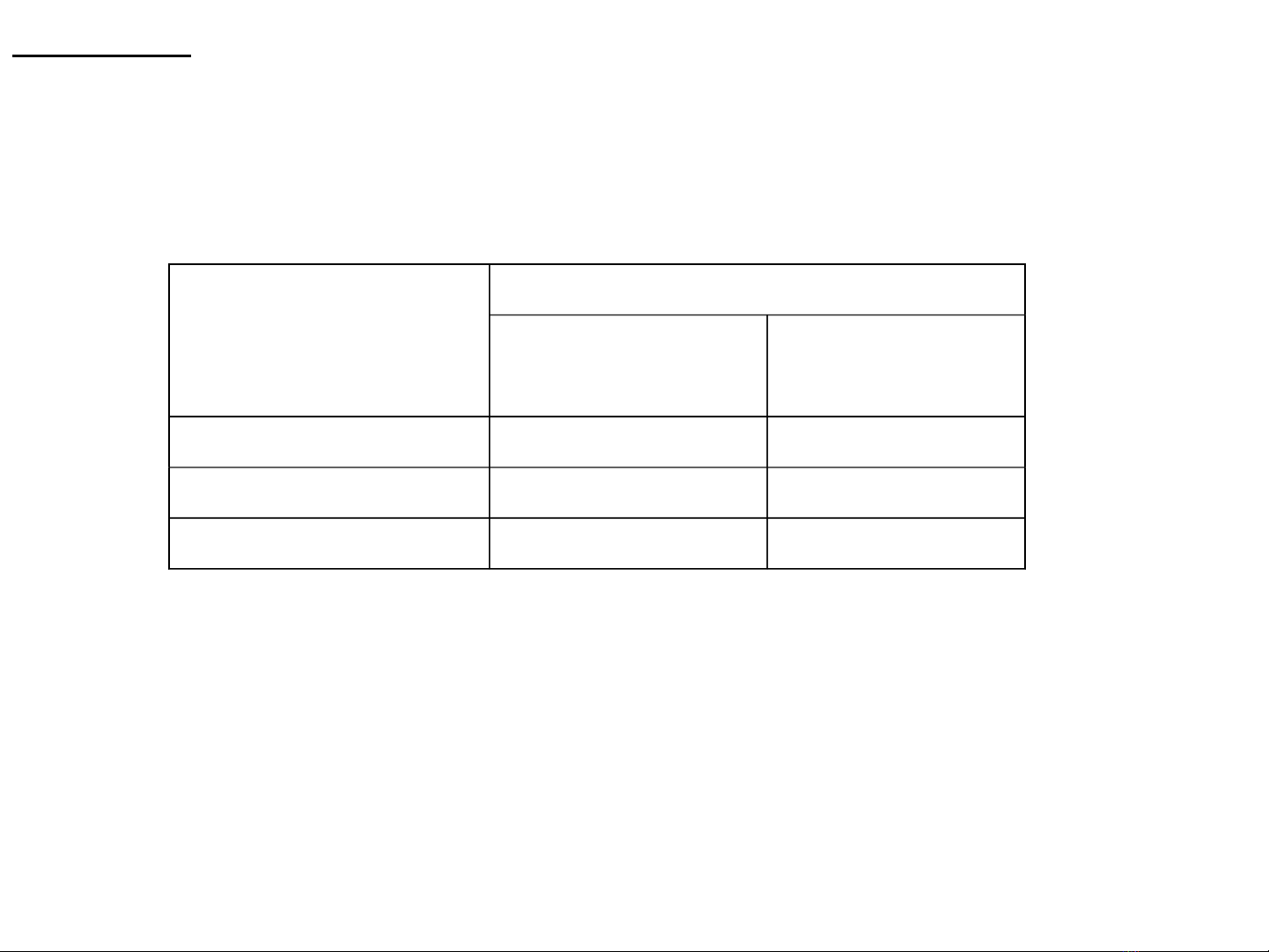
trong 1g thức ăn A và B như sau:
Chất dinh
dưỡng
Thức ăn
A B
Protit (g) 0,1 0,2
Lipit (g) 0,2 0,3
Gluxit (g) 0,6 0,4
Ngoài ra, biết giá của mỗi gam thức ăn A và B tương ứng là
40đ và 60đ.
Hãy lập mô hình bài toán xác định khối lượng thức ăn cần
mua trong ngày sao cho tổng chi phí để mua các loại thức
ăn là thấp nhất.
