Bài giảng Phương pháp tối ưu trong kinh tế: Chương 3 - Nguyễn Phương

Tài liệu 'Chương 3: Các Bài Toán Đồ Thị Mạng' là một tài liệu học thuật về lý thuyết đồ thị, chứng kiến sự áp dụng của nó trong lĩnh vực toán học ứng dụng. Nội dung bao gồm các khái niệm cơ bản về đồ thị, các loại đồ thị và các bài toán tối ưu như bài toán tìm đường đi ngắn nhất bằng thuật toán Dijkstra, và bài toán dòng cực đại giải quyết bằng thuật toán Ford-Fulkerson.

Sinh viên lớp học toán học ứng dụng, nhà nghiên cứu về lý thuyết đồ thị và các bài toán tối ưu đa mạng, hoặc doanh nghiệp cần phải quản lý và tối ưu hóa lưu lượng trong hệ thống học làm việc.

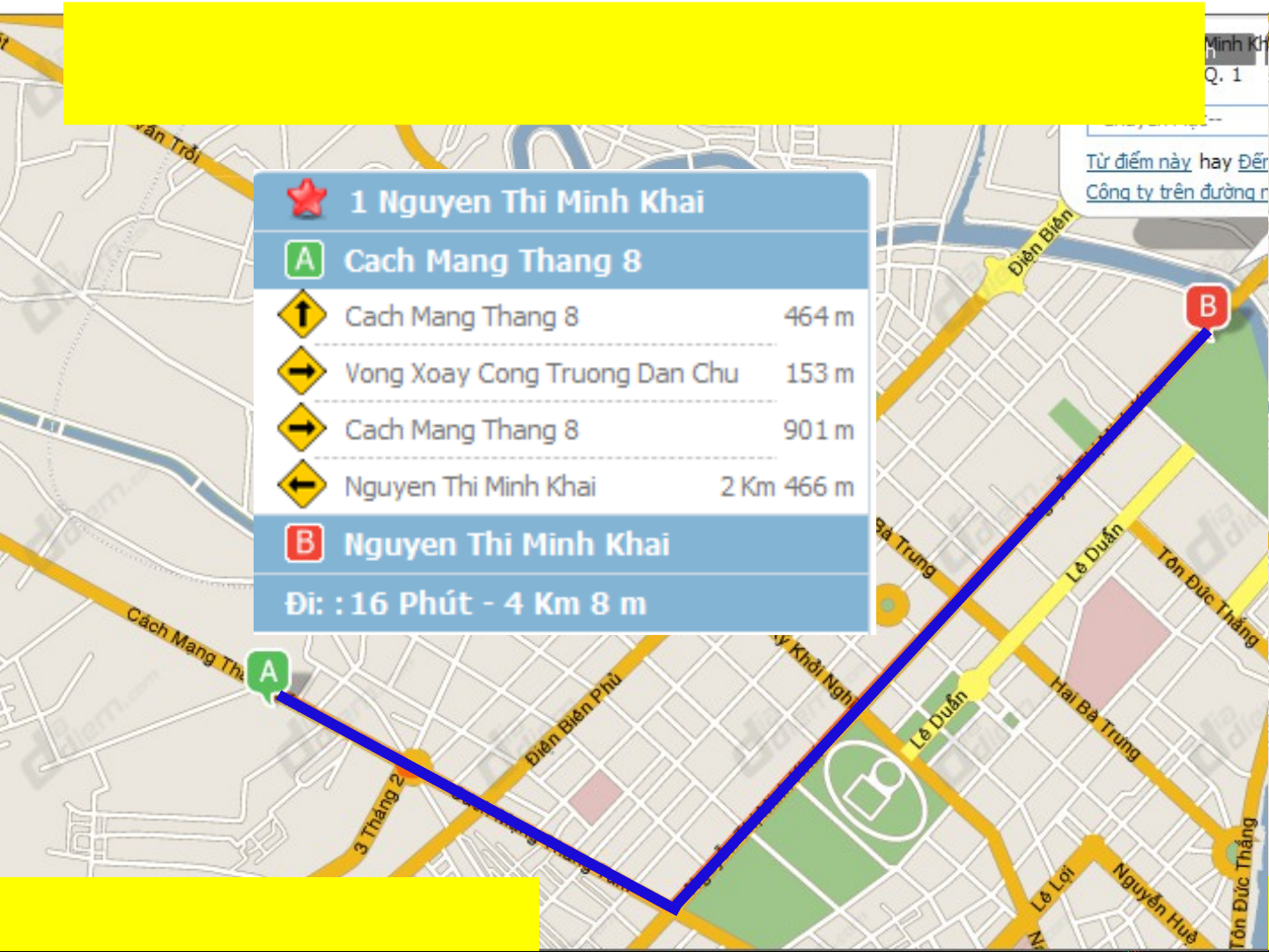
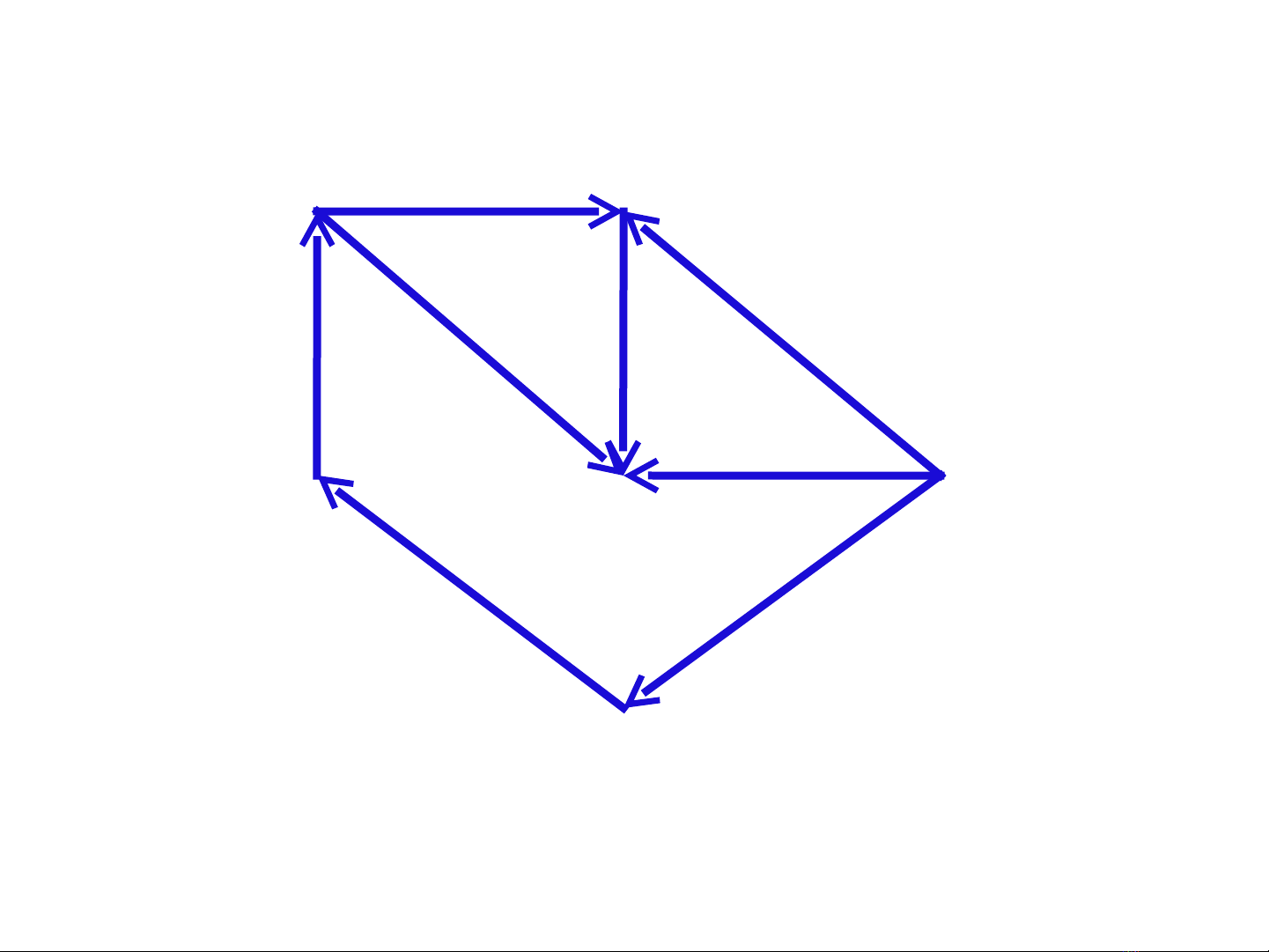
Tài liệu 'Chương 3: Các Bài Toán Đồ Thị Mạng' tập trung vào hai bài toán cơ bản trong lĩnh vực lý thuyết đồ thị, khẳng định nó là một phần quan trọng của toán học ứng dụng. Bài toán tìm đường đi ngắn nhất bằng thuật toán Dijkstra được giới thiệu với một số ví dụ cụ thể trong cuối cùng của tài liệu. Nó là một giải pháp tốt đối với việc tìm đường đi ngắn nhất từ điểm A đến điểm B trong một đồ thị. Tiếp theo, tài liệu giới thiệu bài toán dòng cực đại và sử dụng thuật toán Ford-Fulkerson để giải quyết nó. Bài toán này có thể liên quan đến lưu lượng nước, khí hoặc dầu qua mạng lưới đường ống; lưu lượng biểu mẫu qua hệ thống xử lý giấy; lưu lượng giao thông qua mạng lưới đường bộ; hoặc lưu lượng sản phẩm qua hệ thống dây chuyền sản xuất. Thuật toán Ford-Fulkerson được áp dụng để tối đa hóa lưu lượng qua mạng lưới phân phối của công ty từ nhà máy đến khách hàng, hoặc tối đa hóa lưu lượng qua mạng lưới cung ứng của công ty từ nhà cung cấp đến nhà máy.