CH NG 4ƯƠ
CH NG 4ƯƠ
TÔN THÂT NĂNG L NG CUA DONG CHAY ƯƠ
TÔN THÂT NĂNG L NG CUA DONG CHAY ƯƠ
Công th c chung cua tôn thât năng l ngư ươ
Công th c chung cua tôn thât năng l ngư ươ
1. CAC KHAI NIÊM
1. CAC KHAI NIÊM
1.1. Chiêu dai t ng đ ng ươ ươ
1.1. Chiêu dai t ng đ ng ươ ươ
i
d
i
i
λ
j
ξ
=
Do đó:
i
λ
i
.d
j
ξ
=
i
: đây g i ℓở ọ i là chi u dài ề
t ng đ ng; mươ ươ
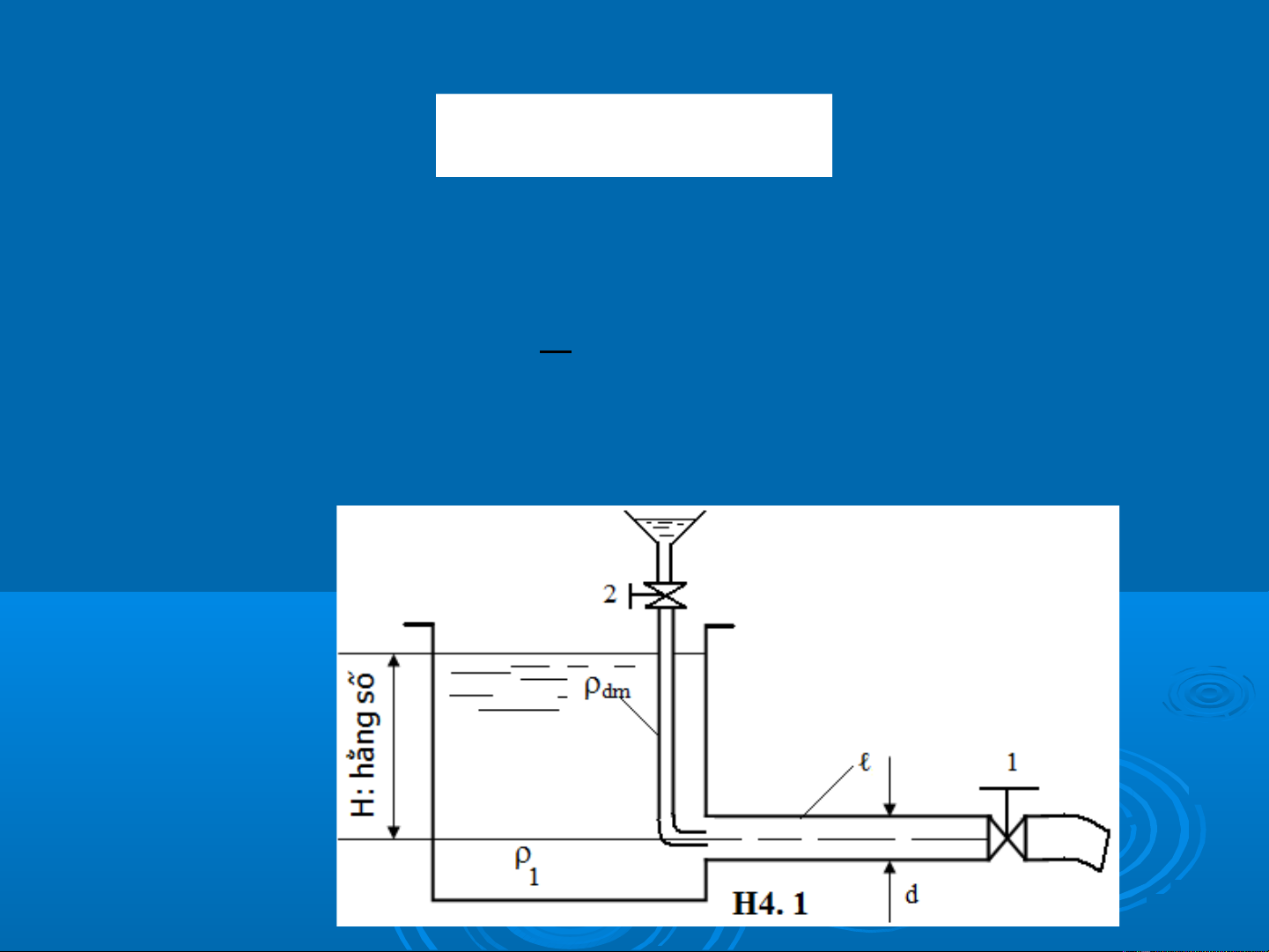
1.2. Chiêu dai quy chiêu đ ng ông dân ươ
1.2. Chiêu dai quy chiêu đ ng ông dân ươ
1.3. Đô nham tuyêt đôi cua ông dân
1.3. Đô nham tuyêt đôi cua ông dân
L = ℓ + Σℓj ; m
ε
d
Đ
ntđ
=
( không có th nguyên)ứ
2. THI NGHIÊM REYNOLDS
2. THI NGHIÊM REYNOLDS
2. THI NGHIÊM REYNOLDS (tt)
2. THI NGHIÊM REYNOLDS (tt)
υµ
ρ
vdvd
Re
==
( không có th nguyên)ứ
T các công trình nghiên c u cho k t lu n:ừ ứ ế ậ
-Dòng ch y t ng khi Re < 2320ả ầ
-Dòng ch y quá đ khi 2320 < Re < 10ả ộ 4
-Dòng ch y r i khi Re > 10ả ố 4
Ý nghĩa v t lý c a chu n s Reynolds: ậ ủ ẩ ố Là t s gi a l c ỉ ố ữ ự
quán tính trên l c ma sátự
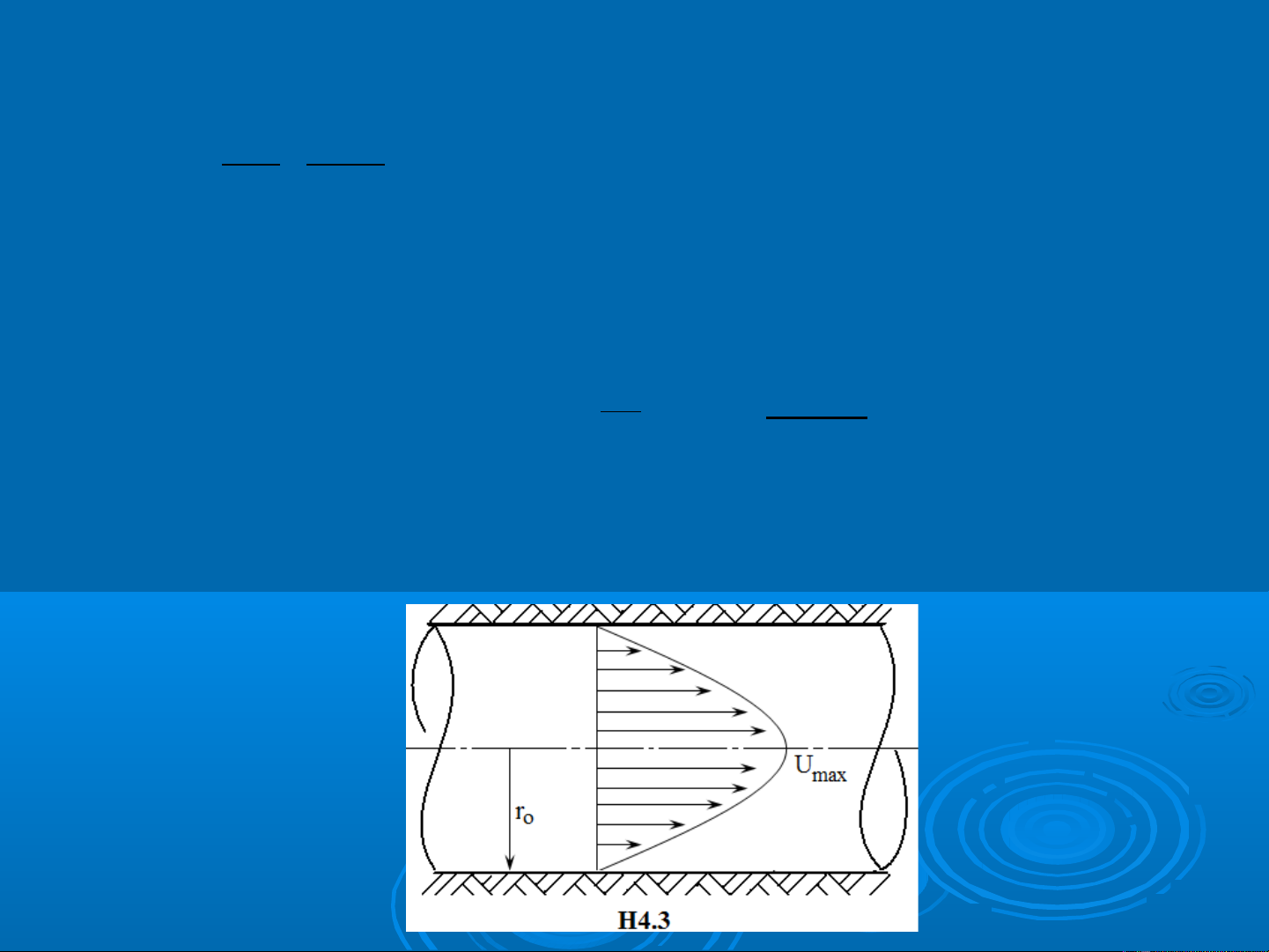
2.1. Dong chay tâng
2.1. Dong chay tâng
2
m
N
;
dr
du
μτ =
D u (-) có ý nghĩa là s ma sát c a các dòng ấ ự ủ
nguyên t s gi m d n t thành ra tâm ngố ẽ ả ầ ừ ố
T đó rút ra quy lu t phân b v n t c nh sau:ừ ậ ố ậ ố ư
−=
2
o
r
r
1
max
UU
s
m
;
Tóm l i v i dòng ch y t ng, quy lu t phân b v n t c theo đ ng ạ ớ ả ầ ậ ố ậ ố ườ
parabol (H4.3)
2.1. Dong chay tâng (tt)
2.1. Dong chay tâng (tt)
• V n t c trung bình c a toàn dòng tính b ngậ ố ủ ằ
s
m
;
2
max
U
v=
• H s Darcy c a dòng ch y t ng tính b ngệ ố ủ ả ầ ằ
ReRe
64 A
==
λ
A: hê sô ph thu c hình d ng ụ ộ ạ
ti t di n ngế ệ ố
• H s hi u ch nh đ ng năng ệ ố ệ ỉ ộ α tính b ngằ
2
A
3
v
A
dA
3
U
α
=
∫
=