Khai niêm: Trong cac thiêt bi cua nganh Công Nghê Hoa
Hoc, th ng găp hiên t ng t ng tac gi a khôi hat va ươ ươ ươ ư
dong l u chât chuyên qua khôi hat đo, ng v i vân tôc ư ư ơ
nao đo thi khôi hat linh đông hăn lên, hiên t ng đo goi ươ
la trang thai tâng sôi cua khôi hat.
S tac đông t ng hô gi a khôi hat va dong l u chât ư ươ ư ư
đanh gia băng chuân sô đông dang Reynolds (cua hat)
υ
=
µ
ρ
=
vdvd
Re
CH NG 9: TRANG THAI TÂNG SÔI KHÔI HATƯƠ
CH NG 9: TRANG THAI TÂNG SÔI KHÔI HATƯƠ
1. CHÊ ĐÔ CHAY
1. CHÊ ĐÔ CHAY
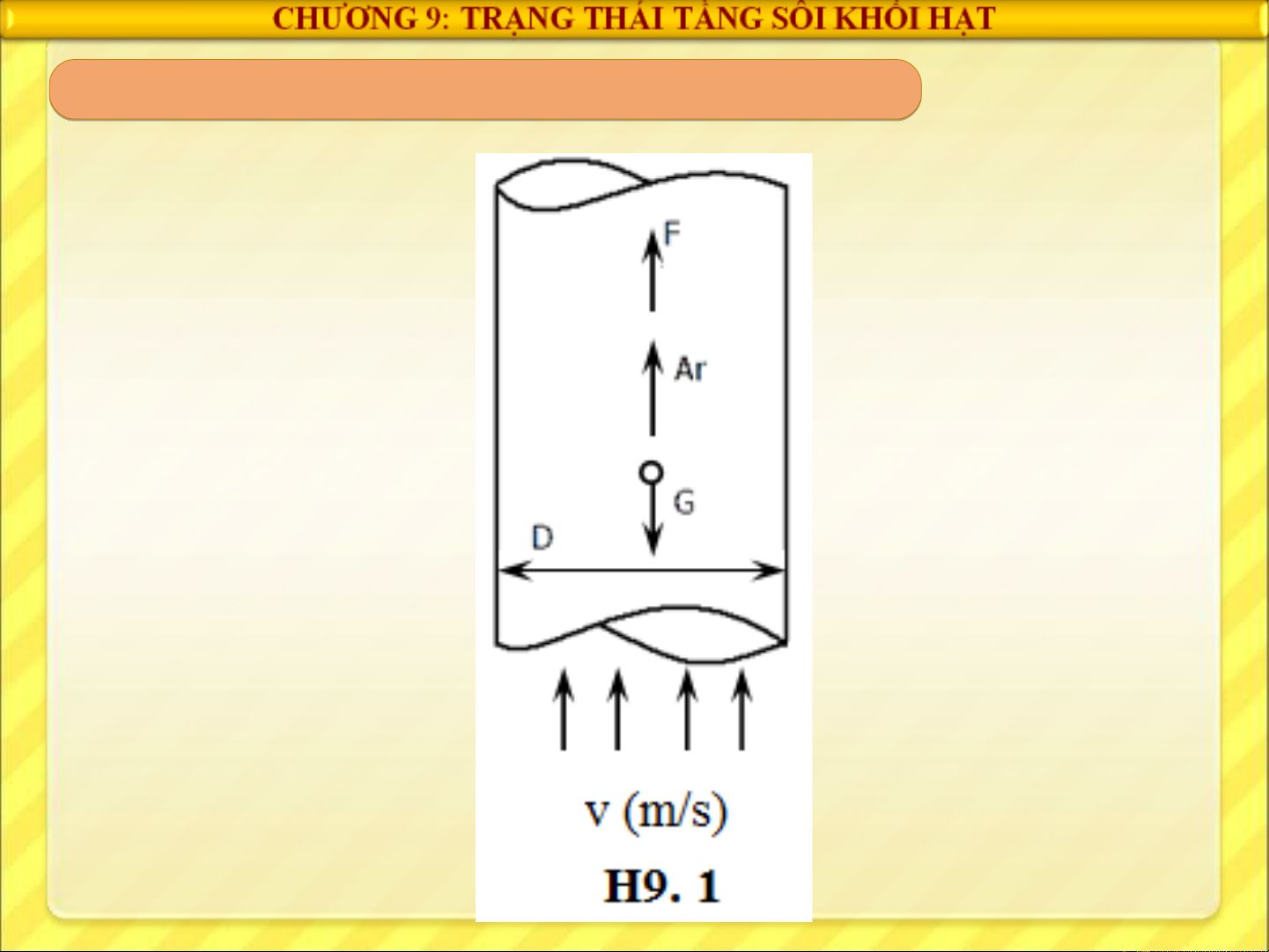
2. VÂN TÔC CÂN BĂNG CUA HAT
2. VÂN TÔC CÂN BĂNG CUA HAT
Khi hat chuyên đông trong ông, hình (H 9.1) se chiu
cac l c sau : ư
• Trong l c G = mg = V ư r.ρr.g; N
• L c đây Archimede Ar = Vư r.ρ.g; N
• L c can môi tr ng ư ươ
N;
2
v
.ρ.A.C=F
2
r
Vân tôc cân băng
Đinh nghia: “ Vân tôc cua dong l u chât theo ph ng ư ươ
đ ng đ a hat vao trang thai cân băng l c, thi vân tôc đo ư ư ư
goi la vân tôc cân băng ”
( )
s/m;
.C
d.g
3
4
=v
r
r
cb
ρ
ρ-ρ
2. VÂN TÔC CÂN BĂNG CUA HAT (tt)
2. VÂN TÔC CÂN BĂNG CUA HAT (tt)
Xet khi:
v = vcb: hat trang thai l l ng ơ ơ ư
v > vcb: hat bi lôi cuôn theo dong chay
v < vcb: hat lăng xuông (xay ra qua trinh lăng)
Công th c tinh vân tôc cân băng co hê sô Cư r la hê sô
tr l c cua hatơ ư
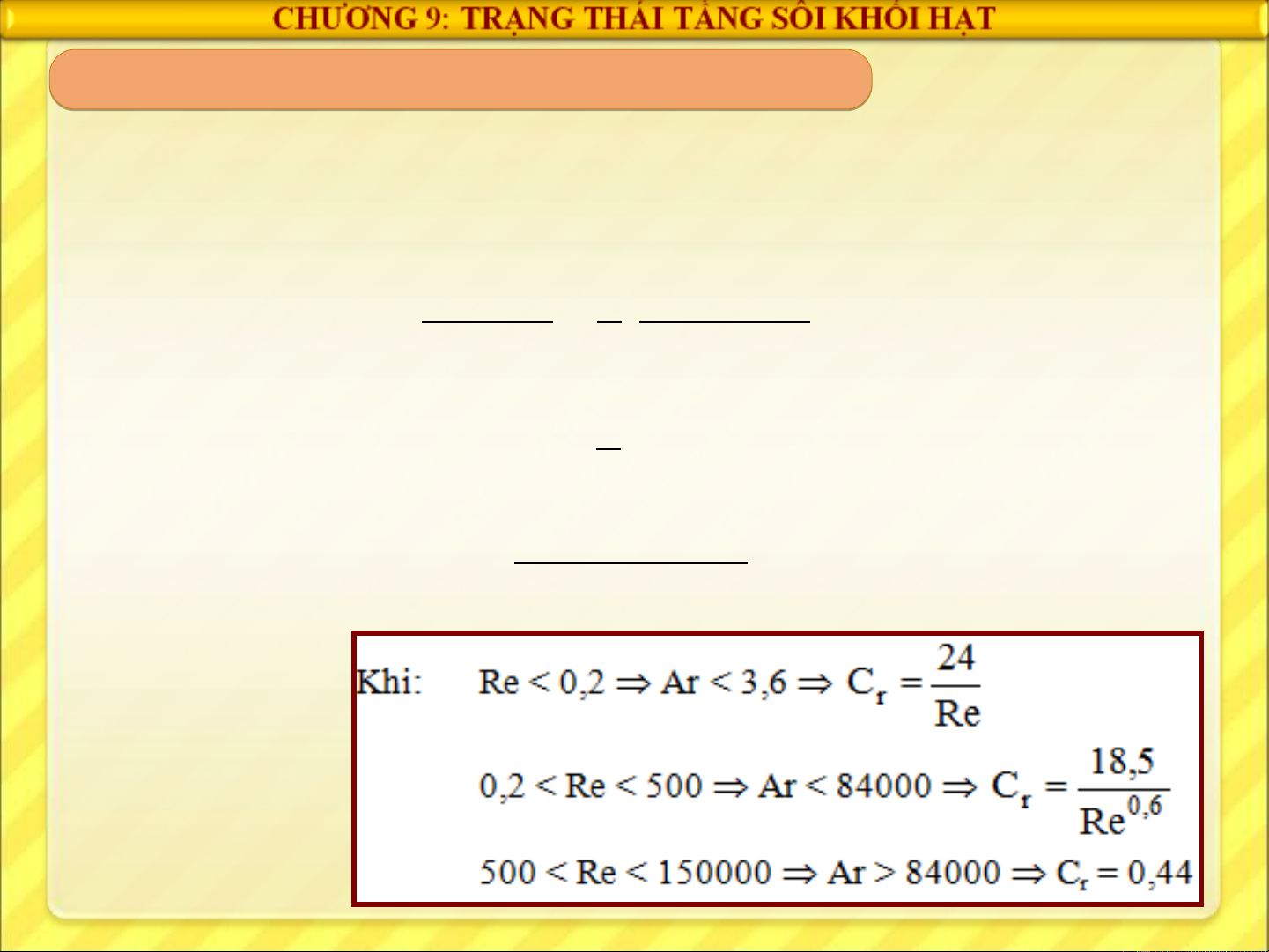
Vung chay tâng:
Vung Alen:
Vung Newton – Rittinger Cr = 0,44
Re
24
C
r
=
6,0
r
Re
5,18
C
=
2. VÂN TÔC CÂN BĂNG CUA HAT (tt)
2. VÂN TÔC CÂN BĂNG CUA HAT (tt)
Chuân sô Archimede
( )
2
r
3
g.d
Ar
µ
ρρ−ρ
=
T (9 – 3) binh ph ng hai vêư ươ
( )
ρ
ρ−ρ
=
ρ
µ
.C
gd
.
3
4
.d
.Re
r
r
22
22
4)-9(Ar
3
4
=C.Re
r
2
đây:Ơ
Thay Re vao
(9 – 4) tim đ c ươ
3. CAC CHUÂN SÔ ĐÔNG DANG
3. CAC CHUÂN SÔ ĐÔNG DANG