Tran Minh Tu – University of Civil Engineering
E-mail: tpnt2002@yahoo.com
8(50)
Chapter 7
®¹i häc
Chương 10
THANH CHỊU LỰC PHỨC TẠP

University of Architechture
10.1. Khái niệm chung
10.2. Thanh chịuuốnxiên
10.3. Thanh chịuuốn và kéo (nén) đồng thời
10.4. Thanh chịu kéo (nén) lệch tâm
Thanh chịulựcp
hứctạp
University of Architechture
10.1. Khái niệm chung (3)
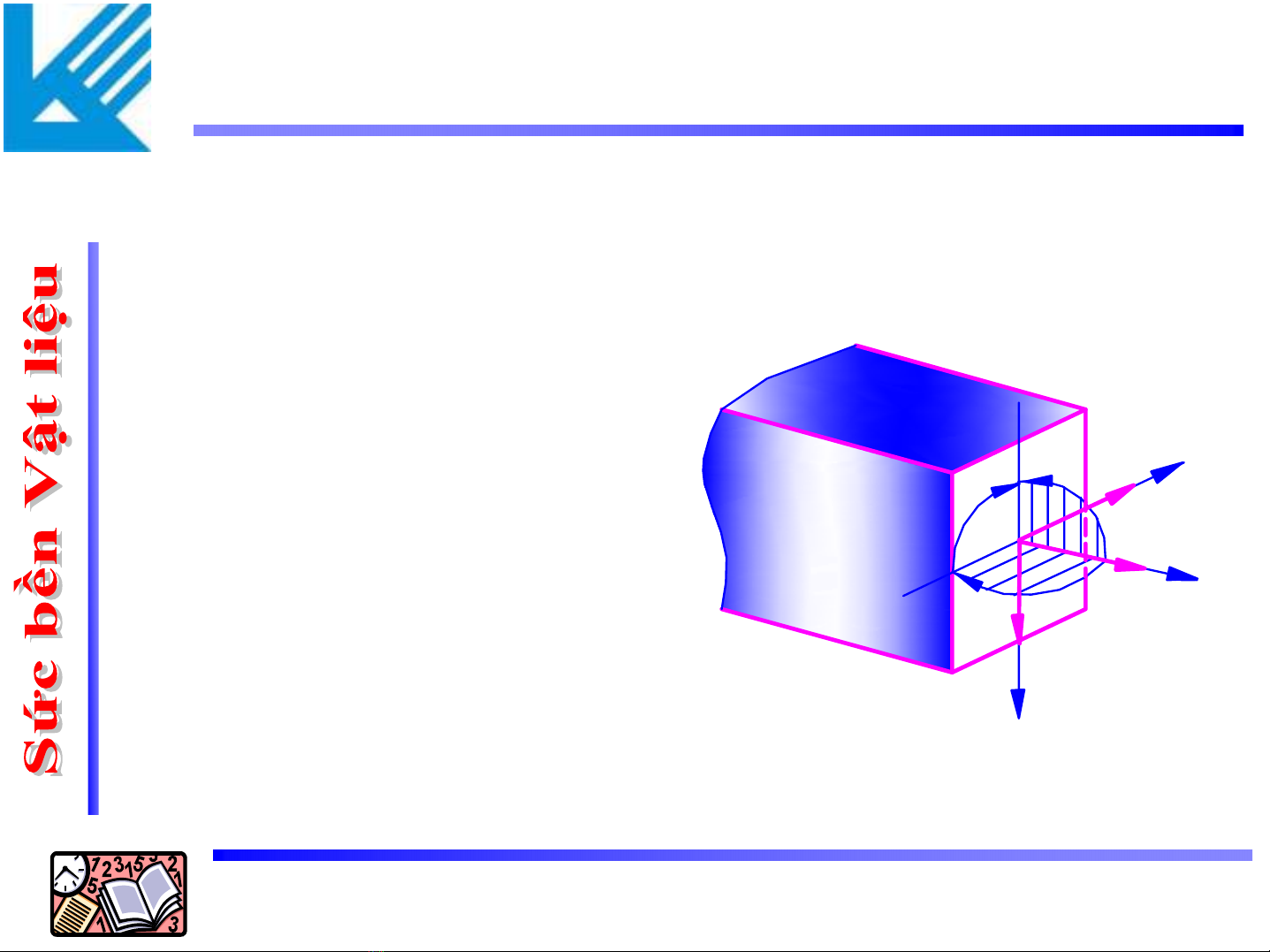
Trong trường hợptổng quát, trên mặtcắt ngang
củamột thanh chịutácdụng củangoạilựcc
ó
sáu ứng lực:
•Lựcdọc: Nz
•Lựccắt: Q
x, Qy
•Mômen uốn: Mx, My
•Mômen xoắn: Mz
Bốnứng lựccơbản:
Nz, Mx, My,Mz
y
z
x
Mx
My
M
zQx
NZ
Q
y
University of Architechture
10.1. Khái niệm chung (4)
10.1.1. Chịulựccơbản(đơng
iản)
Trên mặtcắt ngang chỉtồntạimột trong 6 ứng lực
Kéo (nén) đúng tâm: Nz
Xoắnthuần túy: Mz
Uốnthuầntúy:
z
z
N
A
σ
=
z
p
M
I
τ ρ
=
Mxx
z
x
My
I
σ
=
y
z
y
M
x
I
σ
=
My

University of Architechture
10.1. Khái niệm chung (5)
10.1.2. Chịulựcphứctạp
Là tổhợpcủacáctrường hợpchịulựcđơngiản
•Uốn xiên: Chịuuốnđồng thời trong hai mặt
phẳng quán tính chính trung tâm
•Uốn và kéo (nén) đồng thời
•Uốnvàxoắnđồng thời
•Chịulựctổng quát


























