CHƯƠNG 7-
UỐN PHẲNG THANH THẲNG
GVC. Th.s. Lê Hoàng Tuấn
Nội dung:
CHƯƠNG 7-
UỐN PHẲNG THANH
THẲNG
7.1. Khái niệm
7.2. Uốn thuần túy phẳng
7.3. Uốn ngang phẳng
1. KHÁI NIỆM
Trục thanh bị uốn cong.
Thanh nằm ngang dầm, đà.
Ngoại lực: + P, q trục dầm.
+ M mp chứa trục dầm.
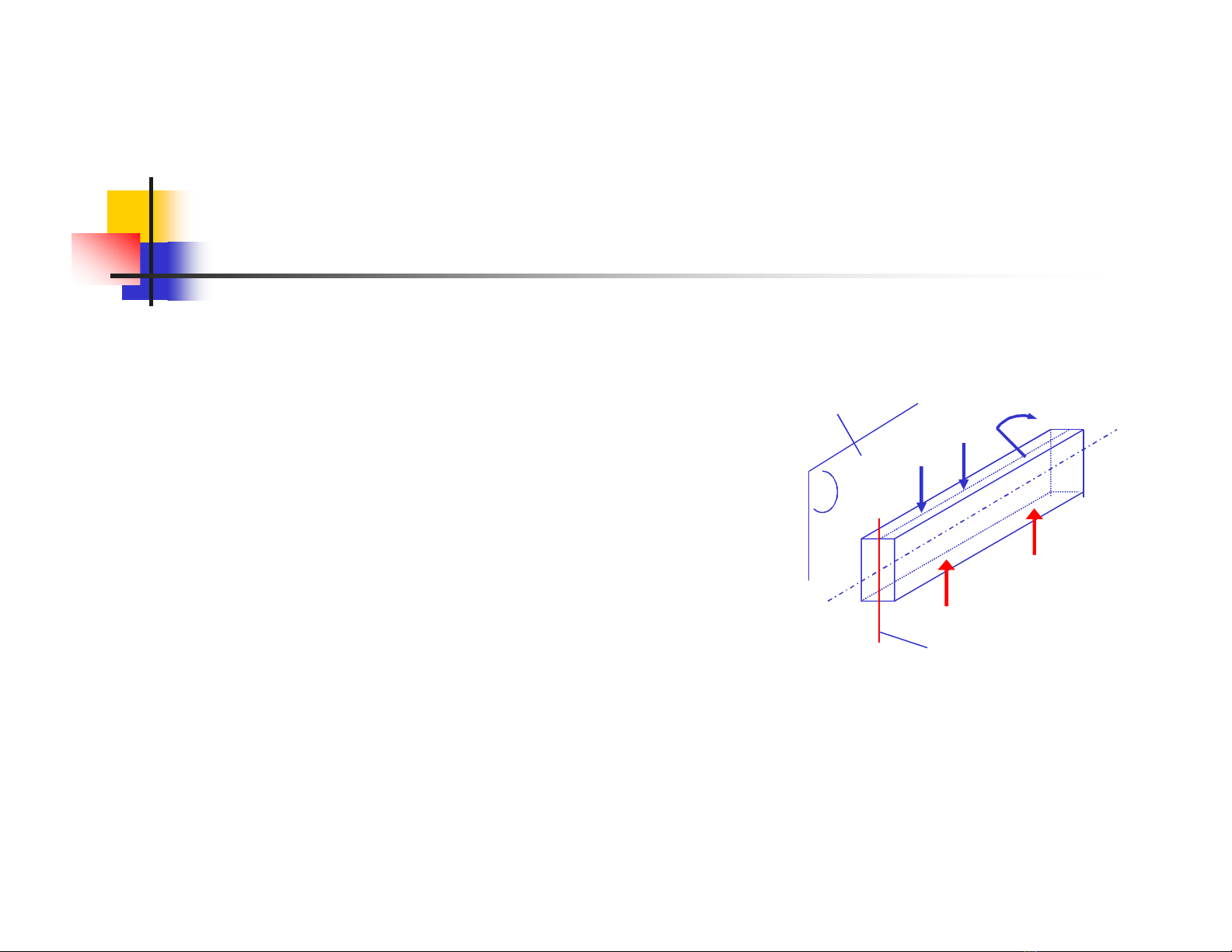
Mặt phẳng tải trọng :
mp chứa tải trọng và trục dầm
Đường tải trọng:
Giao tuyến MPTT và mặt cắt ngang
Mặt phẳng
tải trọng
Đường
tải trọng
P1
V2
V1
P2
M0
1. KHÁI NIỆM
Trục thanh bị uốn cong.
Thanh nằm ngang dầm, đà.
Ngoại lực: + P, q trục dầm.
+ M mp chứa trục dầm.
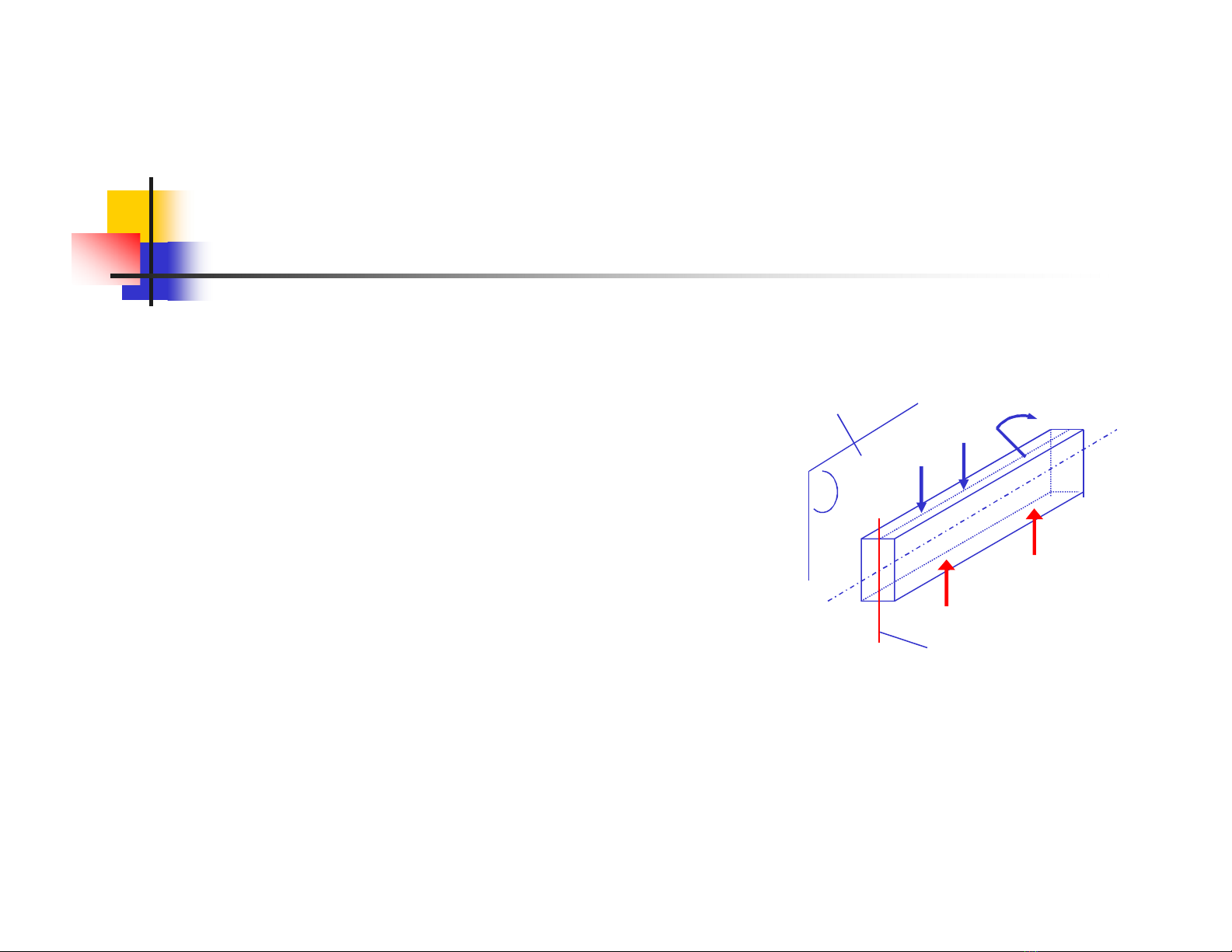
Mặt phẳng tải trọng :
mp chứa tải trọng và trục dầm
Đường tải trọng:
Giao tuyến MPTT và mặt cắt ngang
Mặt phẳng
tải trọng
Đường
tải trọng
P1
V2
V1
P2
M0
1. KHÁI NIỆM
Giới hạn:
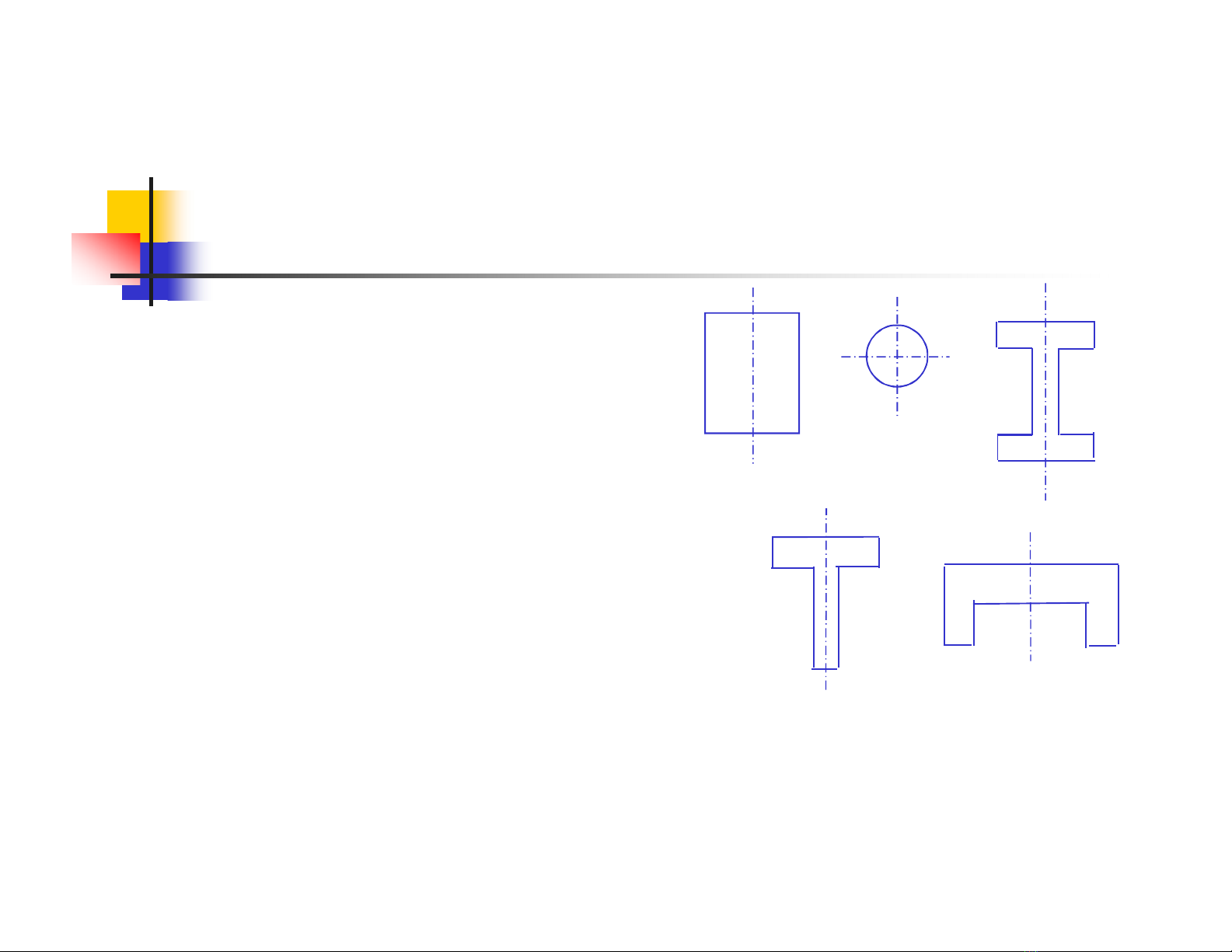
+Mặt cắt ngang có
ít nhất một trục đối xứng.
+Đường tải trọng trục đối xứng
của mặt cắt ngang.
Trục dầm khi cong vẫn mặt phẳng : uốn phẳng.
+Mặt phẳng đối xứng
mp (trục đối xứng, trục thanh).
+Tải trọng MPĐX MPTT
+Chiều rộng m/c ngang bé so với chiều cao
y
y
yy
y


























