Bài giảng Tìm kiếm và trình diễn thông tin: Bài 17 - TS.Nguyễn Bá Ngọc

Chia sẻ: Codon_02 Codon_02 | Ngày: | Loại File: PDF | Số trang:22

Thêm vào BST

Báo xấu

56
lượt xem 6
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Tìm kiếm và trình diễn thông tin: Bài 17 - Phát hiện trùng lặp gần sẽ cung cấp cho các bạn một số vấn đề cơ bản về trùng lặp tuyệt đối; trùng lặp gần; người dùng không mong muốn những kết quả trùng lặp; mô hình tập shingles;...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Tìm kiếm và trình diễn thông tin: Bài 17 - TS.Nguyễn Bá Ngọc

(IT4853) Tìm kiếm và trình diễn thông tin Phát hiện trùng lặp gần
Giảng viên  TS. Nguyễn Bá Ngọc  Địa chỉ: Viện CNTT & TT/BM HTTT/B1-603  Email: ngocnb@soict.hust.edu.vn  Website: http://is.hust.edu.vn/~ngocnb 2
Phát hiện trùng lặp  Trùng lặp tuyệt đối  Dễ dàng loại bỏ, v.d., bằng tổng đại diện.  Trùng lặp gần  Khó phát hiện  Người dùng không mong muốn những kết quả trùng lặp.  Có thể coi một tài liệu vốn phù hợp là không phù hợp nếu lặp lại ngay trong danh sách kết quả. Cần loại bỏ những tài liệu trùng lặp! 3
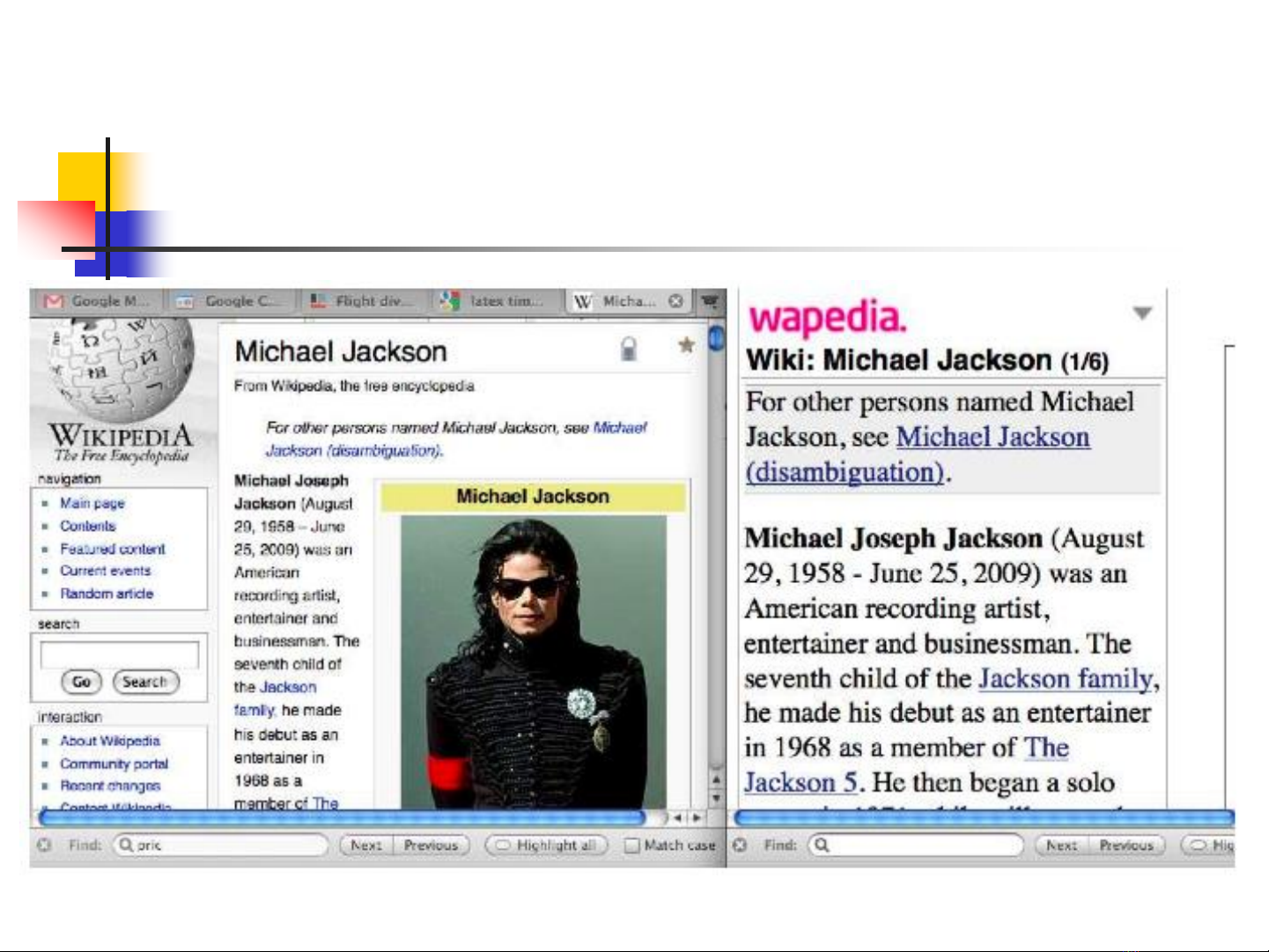
Trùng lặp gần 4
Phát hiện trùng lặp gần  Tính độ tương đồng dựa trên “ký tự”  Rất khó tính độ tương đồng ngữ nghĩa  Những văn bản cùng nội dung nhưng được diễn đạt khác nhau không phải trùng lặp.  Sử dụng ngưỡng θ để kết luận “trùng lặp”.  Ví dụ, Coi hai tài liệu là trùng lặp gần nếu độ tương đồng > 80%. 5
Mô hình tập shingles  Shingle là một n-gram trên từ (bộ n-từ).  Ví dụ, với n = 3, “a rose is a rose is a rose” có mô hình tập shingles như sau:  { a-rose-is, rose-is-a, is-a-rose }  Tính tổng đại diện cho các shingles  Tổng đại diện là các giá trị số trong khoảng 1..2m.  Ký hiệu sk là tổng đại diện của shingle k. Xác định độ tương đồng của hai tài liệu bằng hệ số Jaccard 6
Hệ số Jaccard  Cho hai tập đặc trưng A và B Vớ𝑖 𝐴 ≠ ∅ ℎ𝑜ặ𝑐 𝐵 ≠ ∅, 𝐴∩𝐵 𝐽𝑎𝑐𝑐𝑎𝑟𝑑 𝐴, 𝐵 = 𝐴∪𝐵  Jaccard(A,A) = 1  Jaccard(A,B) = 0 nếu A ∩ B = 0  Miền giá trị là khoảng [0, 1] 7
Ví dụ tính hệ số Jaccard  Cho ba tài liệu: d1: “Jack London traveled to Oakland” d2: “Jack London traveled to the city of Oakland” d3: “Jack traveled from Oakland to London”  Hãy tính hệ số Jaccard J(d1, d2) và J(d1, d3) sử dụng các bộ 2-từ (shingle với kích thước bằng 2)? 8
Ví dụ tính hệ số Jaccard  Cho ba tài liệu: d1: “Jack London traveled to Oakland” d2: “Jack London traveled to the city of Oakland” d3: “Jack traveled from Oakland to London”  Hãy tính hệ số Jaccard J(d1, d2) và J(d1, d3) sử dụng các bộ 2-từ (shingle với kích thước bằng 2)? J(d1, d2) = 3/8 = 0.375; J(d1, d3) = 0 Hệ số Jaccard rất nhạy cảm với trật tự từ 9
Biểu diễn khung của văn bản  Biểu diễn khung (sketch) – là tập con kích thước cố định của tập shingles với, v.d., n = 200.  Được xác định dựa trên một tập hợp các thao tác trộn π1 . . . π200.  Sketch của d được định nghĩa là: < mins ∈d π1(s),mins ∈d π2(s), . . . ,mins∈d π200(s) > 10
Phép trộn và giá trị cực tiểu tài liệu 1: {sk} tài liệu 2: {sk} Sử dụng mins∈d1 π(s) = mins∈d2 π(s) như phép thử tính trùng lặp của d1 và d2 . Trong trường hợp này phép trộn π khẳng định: d1 ≈ d2 11
Hệ số Jaccard trên biểu diễn khung  Sketches  Mỗi tài liệu là một vec-tơ với n = 200 số.  Dễ xử lý hơn so với tập shingles  Chúng ta tính hệ số Jaccard bằng cách nào? 12
Hệ số Jaccard trên biểu diễn khung  Đặt U là hợp các shingles của d1 và d2, còn I là giao  Có |U|! phép trộn trên U  Với s′ ∈ I , có bao nhiêu phép trộn π để argmins∈d1 π(s) = s′ = argmins∈d2 π(s)?  Trả lời: (|U| − 1)!  Có (|U| − 1)! phép trộn cho mỗi s trong I ⇒ |I |(|U| − 1)! phép trộn thỏa mãn argmins∈d1 π(s) = argmins∈d2 π(s)  Như vậy, tỉ lệ phép trộn thỏa mãn mins∈d1 π(s) = mins∈d2 π(s) là: 13
Ước lượng hệ số Jaccard  Hệ số Jaccard bằng tỉ lệ phép trộn thành công.  Phép trộn π là thành công nếu mins ∈d1 π(s) = mins ∈d2 π(s)  Ước lượng xác suất trộn thành công  Sử dụng n phép chộn, v.d., n = 200  Đếm số lượng k phép trộn thành công  k/n được coi như J(d1, d2). 14
Cài đặt  Sử dụng hàm băm như phép trộn: hi : {1..2m} → {1..2m}  Với n = 200, cần n hàm băm  Với mỗi hi cần xác định các giá trị cực tiểu  Đếm số phép trộn thành công k  Giá trị gần đúng của độ tương đồng là k/n. 15
Ví dụ Kết quả trộn Cực tiểu 16
Bài tập Cho mô hình tập shingle của văn bản Hãy ước lượng hệ số Jaccard: J(d1, d2), J(d1, d3), J(d2, d3) 17
Đáp án h(x) = 5x + 5 mod 4 g(x) = (3x + 1) mod 4 Các biểu diễn khung 18
Đáp án 19
Tổng kết  Đầu vào: N tài liệu  Lựa chọn kích thước bộ n-từ, ví dụ, n = 5  Sử dụng 200 phép trộn ngẫu nhiên (200 hàm băm)  Tính N biểu diễn khung 𝑁 𝑁−1  Tính độ phù hợp theo cặp 2  Kết luận trùng lăp gần với độ tương đồng > θ  Bỏ qua các trùng lặp khi đánh chỉ mục 20