
Ch5. KÝ HIỆU TINH THỂ
5.1. Định luật hữu tỷ của các tỷ số giữa các thông số
5.2. Ký hiệu mặt tinh thể
5.3. Định trục cho tinh thể.

Ch5. KÝ HIỆU TINH THỂ
@Để có khái niệm đầy đủ về tinh thể, ngoài việc xác
định tính đối xứng, hình đơn, người ta còn phải ký
hiệu tinh thể.
Ch5. KÝ HIỆU TINH THỂ
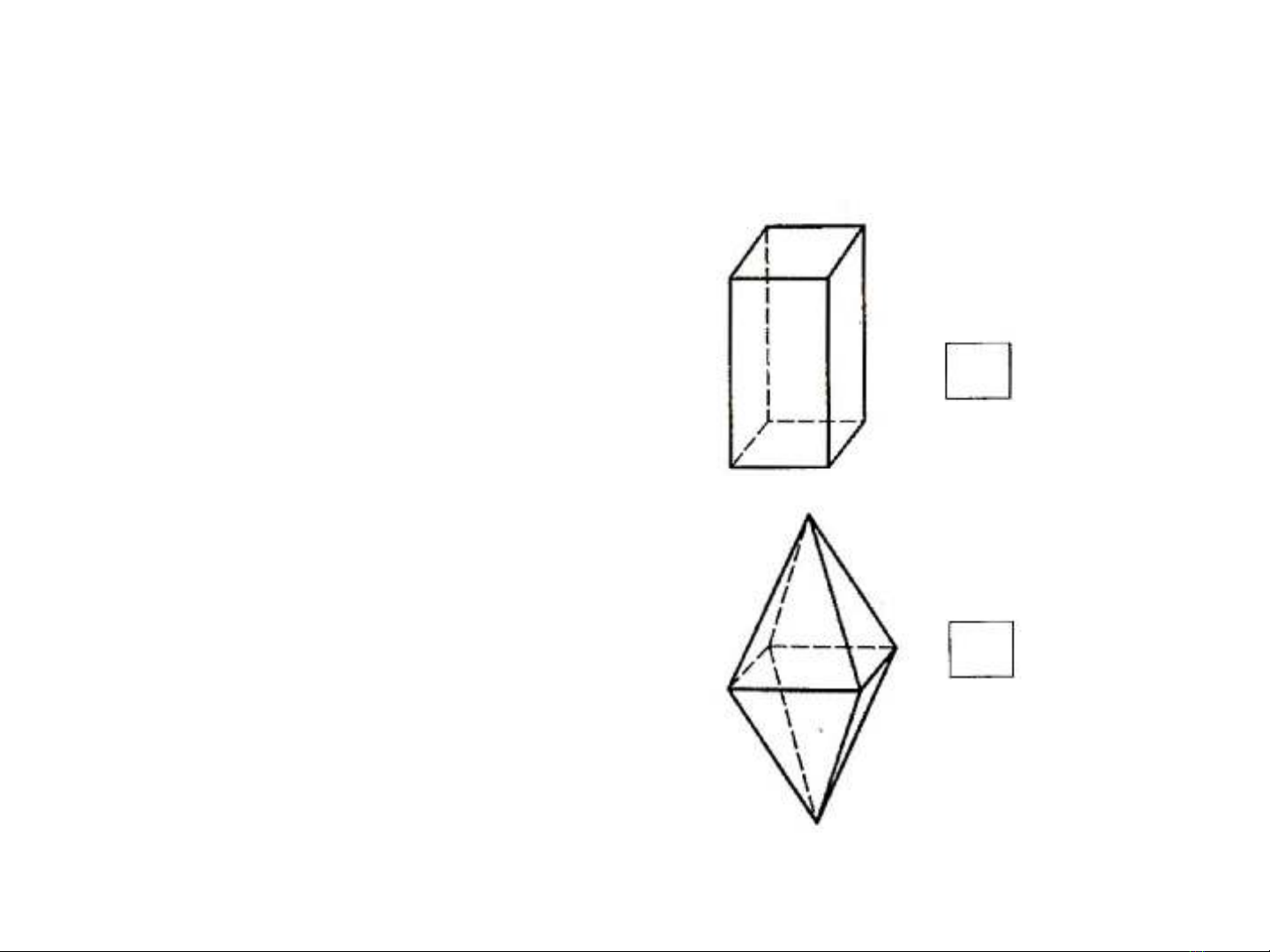
+Hình lăng trụ bốn
phương và tháp đôi bốn
phương.
+Cùng lớp đối xứng
(L44L25PC).
+Hình dạng khác nhau.
Ký hiệu tinh thể thông
qua vị trí tương đối
trong không gian của
các mặt tinh thể.
5.1. Định luật hữu tỷ của các tỷ số
giữa các thông số
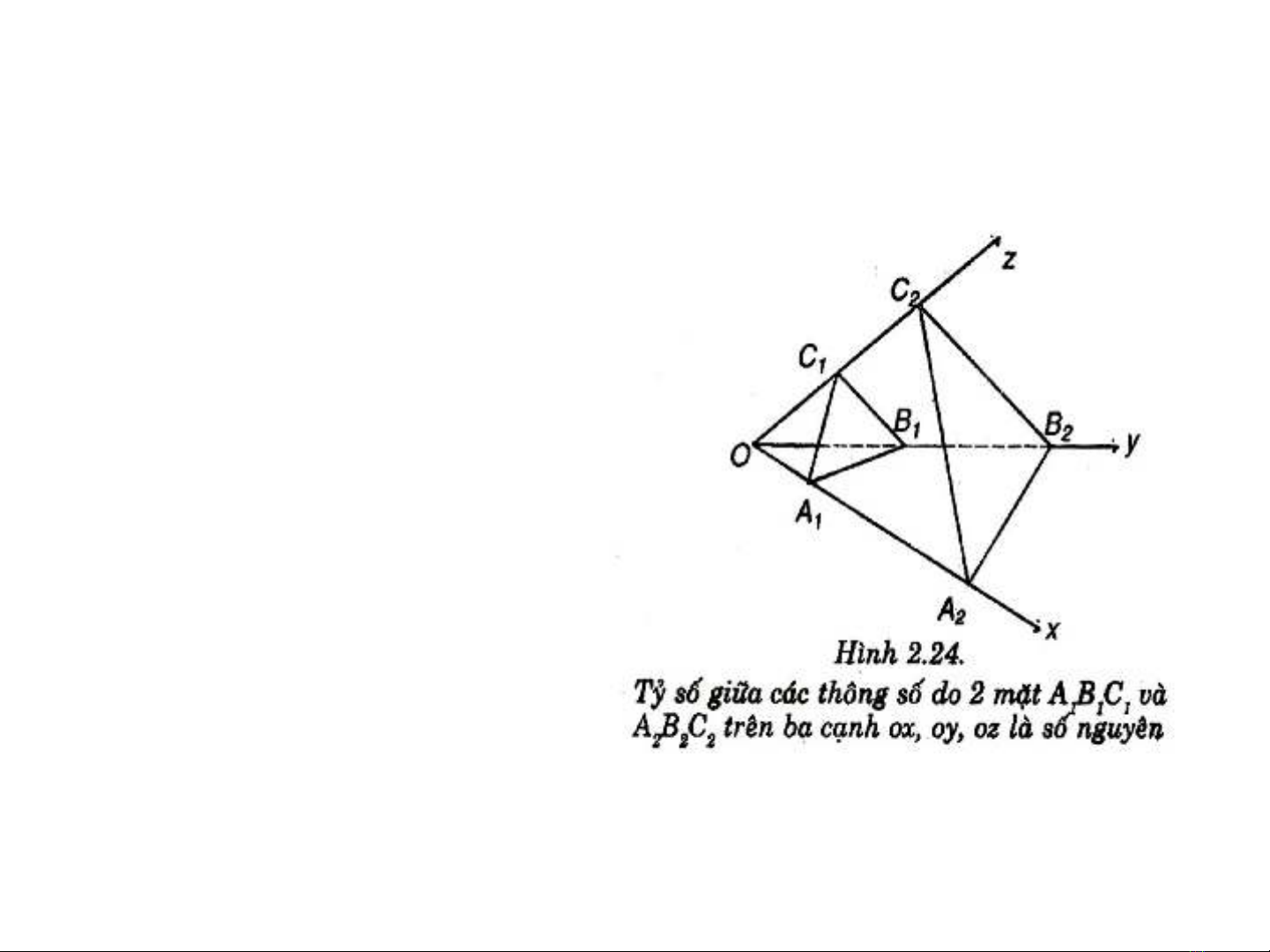
+Ba cạnh của tinh thể
OX, OY và OZ gặp
nhau tại O;
+Hai mặt A1B1C1và
A2B2C2không song
song nhau và cắt 3 cạnh
đó;
5.1. Định luật hữu tỷ của các tỷ số
giữa các thông số
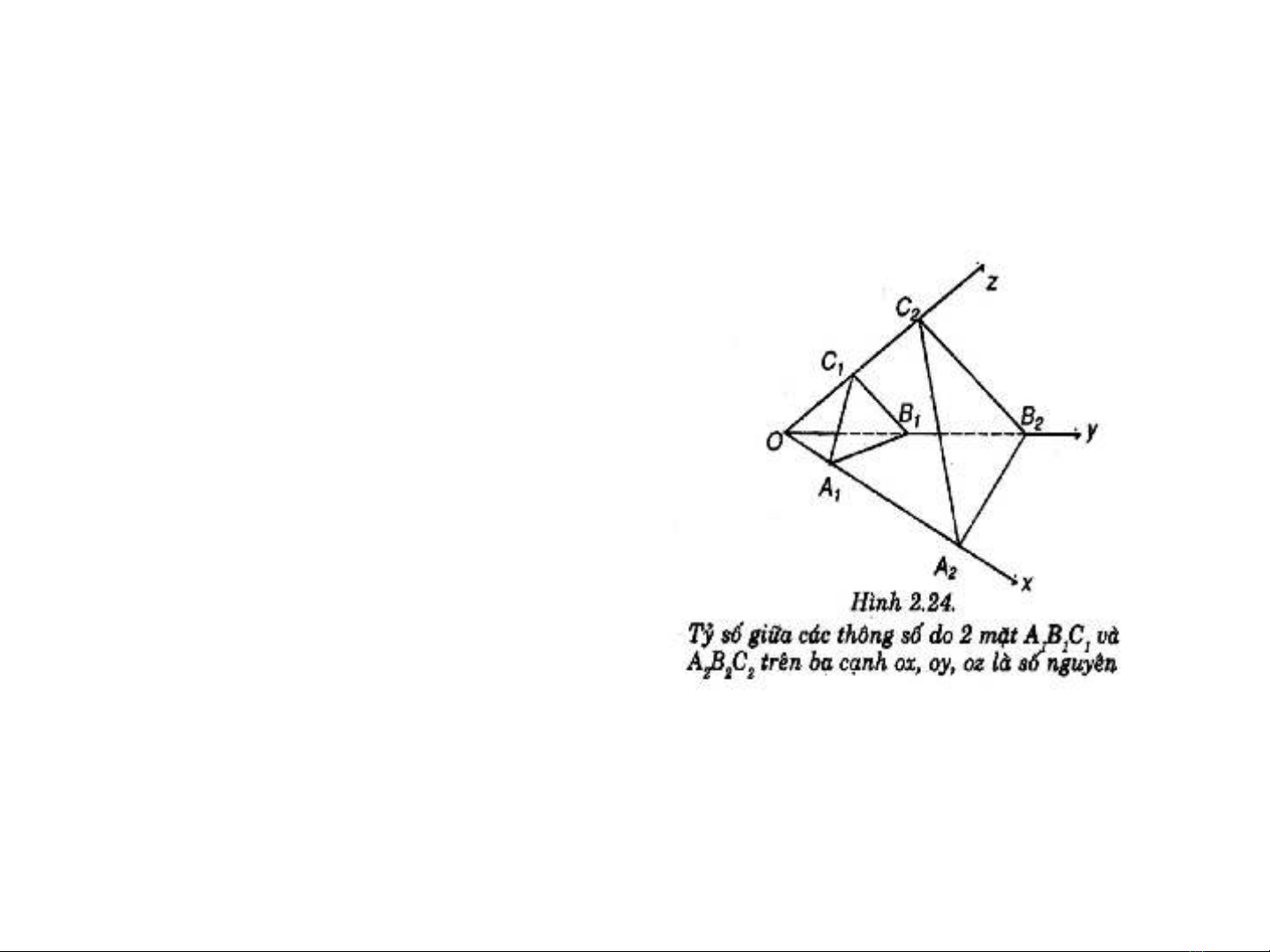
+OA, OB, OC là thông số
của mặt thứ nhất (a,b,c)
và OD, OE, OF là thông
số của mặt thứ hai
(d,e,f).
+Lập tỉ số kép:
OD/OA: OE/OB: OF/ OC
= p : q : r thì p, q, r
cũng là những số
nguyên không lớn lắm


























