
Cây
Biên so n: TS.Nguy n Vi t Đôngạ ễ ế

Cây
1. ĐN và tính ch tấ
2. Cây khung ng n nh tắ ấ
3. Cây có g cố
4. Phép duy t câyệ
2

Đnh nghĩa và tính ch tị ấ
a) Cho G là đ th vô h ng. G đc g i là ồ ị ướ ượ ọ m t cây ộ
n u G liên thông và không có chu trình s c p.ế ơ ấ
b) R ng ừlà đ th mà m i thành ph n liên thông c a ồ ị ỗ ầ ủ
nó là m t cây.ộ
Đnh nghĩa Cây.ị
3
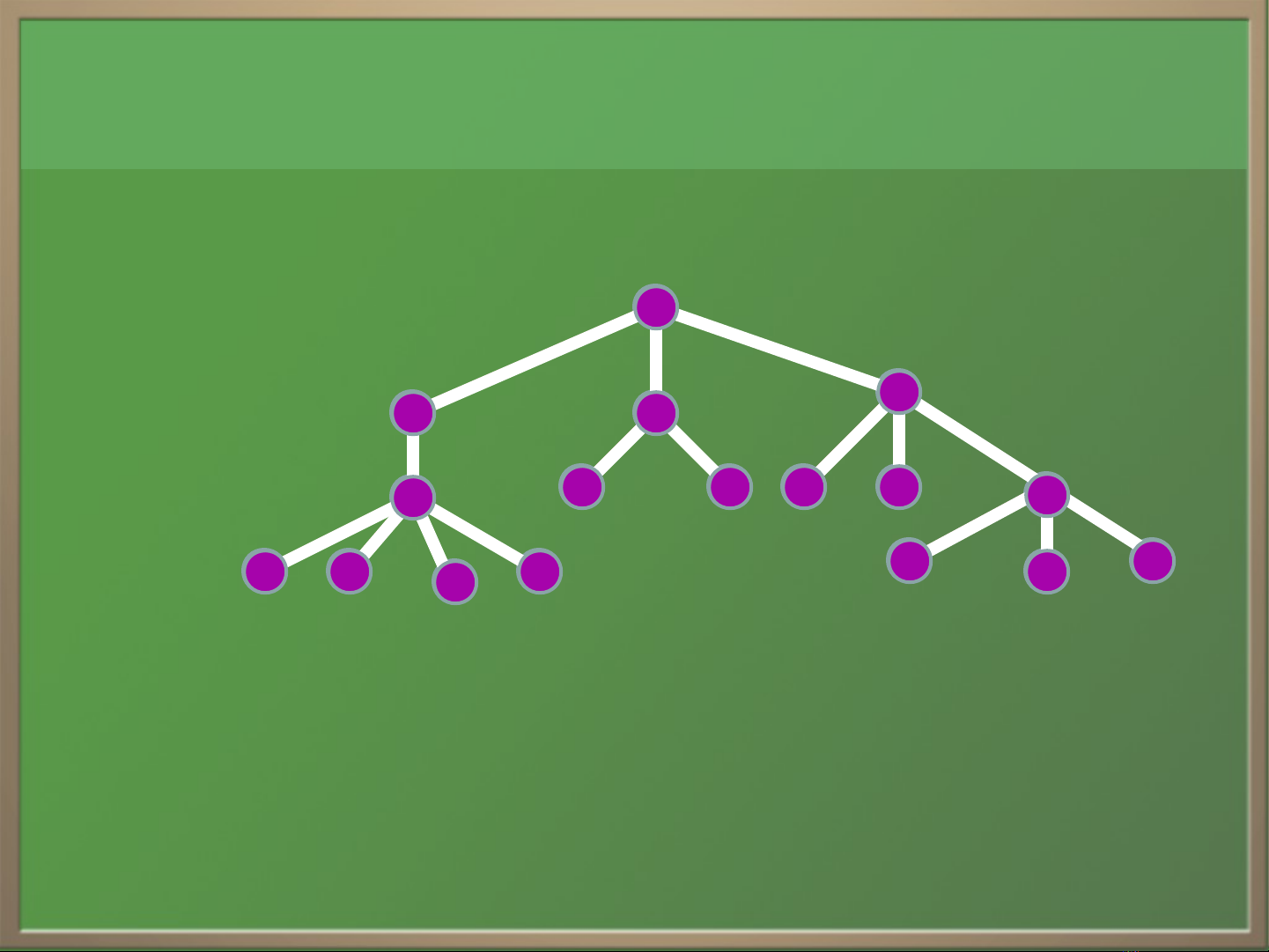
11
234
10
5
6 7 89
12 13 14 15 16 17
1
234
10
5
6 7 89
11 12 13 14 15 16 17
1
Đnh nghĩa và tính ch tị ấ
4

Đnh nghĩa và tính ch tị ấ
Cho T là đ th vô h ng có n đnh. Các phát bi u sau ồ ị ướ ỉ ể
đây
là t ng đng:ươ ươ
i. T là cây.
ii. T liên thông và có n-1 c nh.ạ
iii. T không có chu trình s c p và có n-1 c nh .ơ ấ ạ
iv. T liên thông và m i c nh là m t c u.ỗ ạ ộ ầ
v. Gi a hai đnh b t k có đúng m t đng đi s c p ữ ỉ ấ ỳ ộ ườ ơ ấ
n i chúng v i nhau.ố ớ
T không có chu trình s c p và n u thêm vào m t ơ ấ ế ộ
Đi u ki n c n và đ.ề ệ ầ ủ
5





![Bài giảng Toán rời rạc 1: Bài toán đếm - Ngô Xuân Bách [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20241231/tambang1206/135x160/431735607183.jpg)









![Đề thi kết thúc học phần Nguyên lí Hóa học 2 [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251014/anhinhduyet000/135x160/69761760428591.jpg)










