Chương VII.
TRÒ CHƠI ĐỘNG
BiÓu diÔn d¹ng më réng cña mét trß ch¬i
NÕu ta biÕt nh÷ng ngêi ch¬i, c¸c quy t¾c, c¸c kÕt côc
vµ c¸c thu ho¹ch, th× ta cã thÓ biÓu diÔn trß ch¬i mét
c¸ch h×nh thøc theo c¸i mµ ta gäi lµ d¹ng më réng.
D¹ng më réng th©u tãm viÖc ai ®i khi nµo, mçi ngêi
ch¬i cã thÓ lµm hµnh ®éng g×, nh÷ng ngêi ch¬i biÕt g×
khi ®i, kÕt côc nh mét hµm cña c¸c hµnh ®éng thùc
hiÖn bëi c¸c nh÷ng ngêi ch¬i lµ g×, vµ thu ho¹ch cña
nh÷ng ngêi ch¬i tõ mçi kÕt côc cã thÓ.
Thí dụ về cây trò chơi
Cây gồm các đỉnh theo thứ tự của nước đi
Nhánh thể hiện các chiến lược hay nước đi có
thể có
Thu hoạch nhận được sau khi kết thúc nước đi
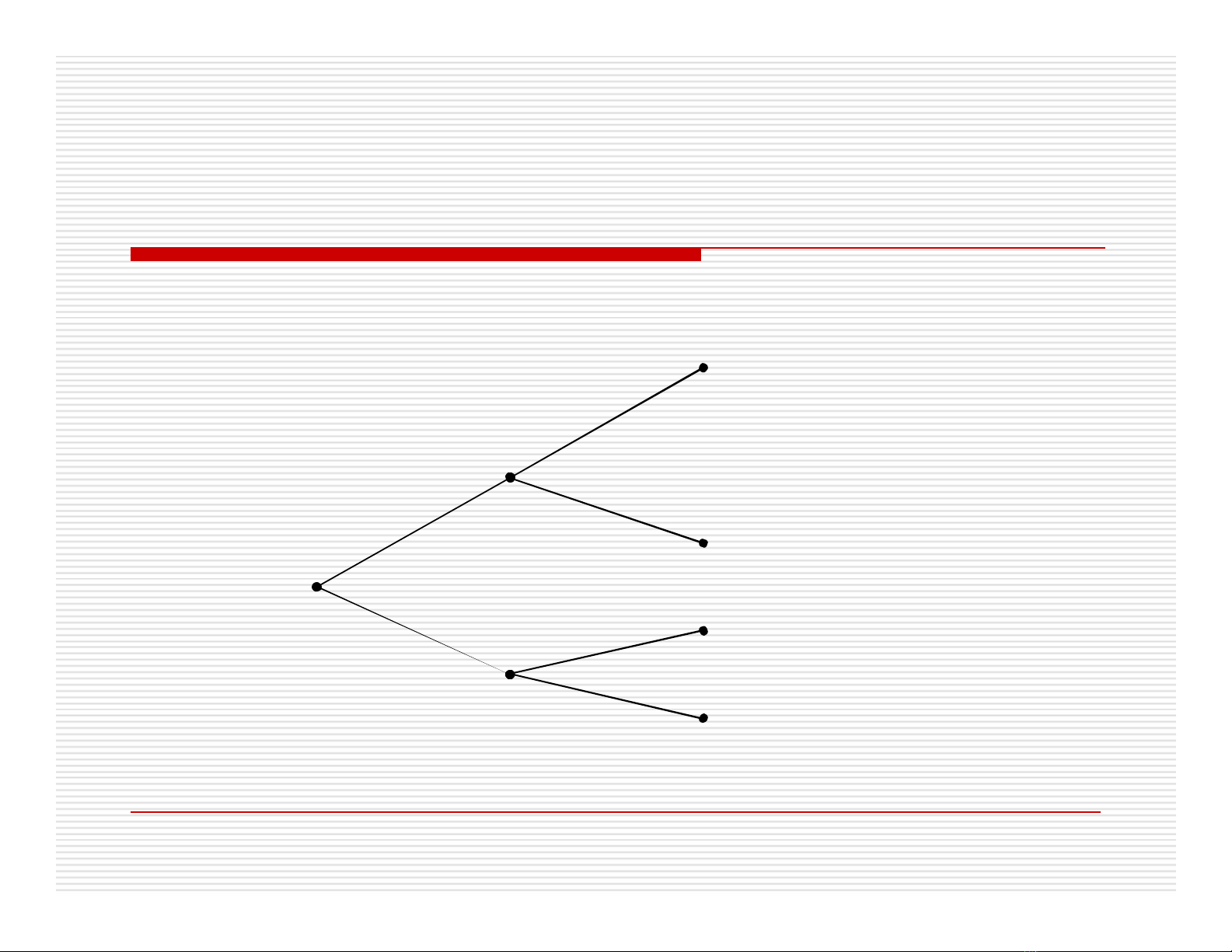
Cây trò chơi
.
A
L
H
B
L
L
H
H
B
7.5
5.4
6.4
6.3
Trß ch¬i qu¶ng c¸o
H×nh 1 minh ho¹ c¸c chi tiÕt ®Æc trng cña trß ch¬i
qu¶ng c¸o. Trong “c©y” trß ch¬i nµy, hµnh ®éng ®i
tõ tr¸i sang ph¶i, vµ mçi “nót” biÓu diÔn mét quyÕt
®Þnh ®èi víi c«ng ty ®îc chØ ra t¹i ®ã.
Níc ®i thø nhÊt trong trß ch¬i nµy thuéc vÒ c«ng
ty A: Nã ph¶i chän møc chi tiªu qu¶ng c¸o cña nã,
H hoÆc L.
V× c¸c quyÕt ®Þnh cña c«ng ty B x¶y ra bªn ph¶i
quyÕt ®Þnh cña c«ng ty A, c©y nµy chØ ra r»ng c«ng
ty B ra quyÕt ®Þnh cña m×nh sau c«ng ty A.
Trß ch¬i qu¶ng c¸o
ë giai ®o¹n nµy, cã thÓ cã hai phiªn b¶n cña trß
ch¬i tuú thuéc B cã ®îc gi¶ thiÕt lµ biÕt lùa chän
cña A hay kh«ng.
§Çu tiªn, ta sÏ xÐt trêng hîp B kh«ng cã th«ng
tin nµy.
H×nh oval lín bao quanh hai nót quyÕt ®Þnh cña B
chØ r»ng c¶ hai nót cã th«ng tin nh nhau (cïng
kh«ng cã).
C«ng ty B ph¶i chän H hoÆc L mµ kh«ng biÕt A
®· lµm g×. Sau nµy ta sÏ xÐt trêng hîp mµ B cã
th«ng tin nµy.