
TRƯỜNG ĐẠI HỌC KINH TẾ - ĐẠI HỌC ĐÀ NẴNG
400
VAI TRÒ CỦA MẠNG GIÁ TRỊ VÀ LÝ THUYẾT TRÒ CHƠI TRONG
CẠNH TRANH
ROLES OF VALUE NET AND GAME THEORY IN BUSINESS COMPETITION
TS. Nguyễn Xuân Lãn, Nguyễn Hữu Nam Phúc
Trường Đại học Kinh tế - Đại học Đà Nẵng
TÓM TẮT
Nghiên cứu này nhằm làm rõ vai trò của mạng giá trị và lý thuyết trò chơi trong môi trường kinh doanh đầy
cạnh tranh ngày nay. Nghiên cứu so sánh ưu điểm, nhược điểm và các trường hợp ứng dụng của mô hình 5
lực lượng cạnh tranh và mô hình Mạng giá trị. Nghiên cứu cũngtrình bày hai loại trò chơi trong lý thuyết trò
chơi cũng như những hạn chế của lý thuyết này đồng thời đưa ra trường hợp ứng dụng lý thuyết trò chơi của
công ty Apple. Nghiên cứu đã chỉ ra rằng, trong kinh doanh, quan điểm tranh hợp là rất quan trọng và lý
thuyết trò chơi đã và đang được ứng dụng cho việc ra quyết định chiến lược trong môi trường kinh doanh
hiện đại.
Từ khóa: mạng giá trị; lý thuyết trò chơi; cạnh tranh; công ty Apple; quan điểm tranh hợp.
ABSTRACT
This study aims to clarify the role of Value Net and Game Theory in modern business competition. The
paper compares the advantages, disadvantages and applications of Five forces model and Value Net. The
paper also presents two types of games in Game Theory, the limitation of this theory as well as Apple’s case
study. This study indicates that in business, coopetition is very important and Game Theory has been applied
to the strategic decision making in the modern business environment.
Keywords: Value net; game theory; coopetition; Apple Inc; coopetition.
1. Giới thiệu
Giành lợi thế cạnh tranh hay chiến thắng
đối thủ … được xem là mục tiêu của các công
ty khi gia nhập môi trường cạnh tranh. Muốn
vậy, cần tỏ ra khôn ngoan hơn đối thủ, giành
giật quyết liệt thị phần, khuyếch trương thương
hiệu, khống chế nhà cung cấp, khóa chặt khách
hang. Theo quan điểm đó, sẽ luôn có người
thắng và kẻ bại trong kinh doanh. Cách nhìn về
một kết cục thắng - bại được Gore Vidal viết
như sau: “Chỉ thành công thôi chưa đủ. Phải
làm sao cho kẻ khác thất bại nữa”
(A.M.Brandenburger, B.J NaleBuff, 2006)
Tuy nhiên, với những thay đổi từ môi
trường cạnh tranh hiện đại, đặc biệt là sự phát
triển của internet và mạng giá trị, các công ty
không thể tiếp tục nghĩ theo cách như vậy. Họ
cần phải lắng nghe khách hàng, hợp tác với nhà
cung cấp, lập ra các nhóm mua hàng và xây
dựng những quan hê đối tác chiến lược (thậm
chí với cả đối thủ cạnh tranh). Và tất cả những
điều này không hề giống như trong cuộc chiến.
Bernard Baruch – nhà tài phiệt ngân hàng hàng
đầu của thể kỷ XX đã phản đối Gore Vidal:
“Không cần phải thổi tắt ánh sáng của người
khác để mình tỏa sang”.. Kinh doanh là sự hợp
tác khi cần tạo ra chiếc bánh nhưng sẽ là cạnh
tranh khi đến lúc chia phần chiếc bánh đó.
(A.M.Brandenburger, B.J NaleBuff, 2006)
Lý thuyết trò chơi (Game Theory) (Von
Neumann, 1944; Nash, Selten and
Harsanyi,1994; R.Gibbon, 1992) mà nền tảng
ứng dụng là mạng giá trị (Value Net) được
xem là sự tiến triển đáng kể về cách tiếp cận
đối với cân nhắc các quyết định chiến lược khi
mà các quan điểm về cạnh tranh cũng như
phương thức ứng xử trong cạnh tranh trước
đây, chẳng hạn của M.Porter, đã không còn
phù hợp (M.Porter,1980,1985). Nhiều nhà kinh
doanh đã từng nghe nói tới lý thuyết trò chơi
nhưng nghi ngờ không biết đó có thực là một
công cụ đắc lực tiềm tàng hay không. Một

HỘI THẢO VỀ KHOA HỌC QUẢN TRỊ (CMS-2013)
401
phần, ảnh hưởng quan điểm về cạnh tranh của
M.Porter quá lớn, các phân tích và nghiên cứu
về mạng giá trị (Fjeldstad và
Stabell,1998)không nhiều, phần nữa và rất
quan trọng là chính các kỹ năng toán học phức
tạp đã cản trở việc đưa lý thuyết vào thực tiễn.
Hơn nữa, các tác giả của lý thuyết trò chơi
cũng thường không hiểu biết nhiều lắm về thực
tiễn kinh doanh, vì vậy một số điểm trong lý
thuyết của họ không nắm bắt được các thực
tiễn đó và trở thành rào cản cho việc ứng dụng.
Bài nghiên cứu này nhằm làm sáng tỏ vai trò
đối thoại giữa các thể giới của lý thuyết trò
chơi và thực tiễn kinh doanh.
2. Cơ sở lý thuyết
2.1. Mô hình phân tích cạnh tranh: từ Năm
lực lượng cạnh tranh đến Mạng giá trị
Có thể xem Michael E.Porter là tác giả có
ảnh hưởng đáng kể nhất về phân tích cạnh
tranh. Khuôn khổ phân tích nổi tiếng của
M.Porter (1980) là mô hình năm lực lượng
cạnh tranh. Theo Porter, có năm lực lượng định
hướng cạnh tranh trong phạm vi ngành, đó là:
(1) Nguy cơ nhập cuộc của các đối thủ cạnh
tranh tiềm tàng; (2) Mức độ cạnh tranh giữa
các công ty hiện có trong ngành; (3) Sức mạnh
thương lượng của người mua; (4) Sức mạnh
thương lượng của người bán; (5) Đe dọa của
các sản phẩm thay thế.
Porter chỉ ra rằng các lực lượng này càng
mạnh, càng hạn chế khả năng của các công ty
hiện tại trong việc tăng giá và có được lợi
nhuận cao hơn. Mô hình cạnh tranh của Michal
Porter với mục đích đánh giá về ngành mà
công ty đang kinh doanh, có hấp dẫn hay
không, yếu tố then chốt cho thành công và dẫn
dắt sự thay đổi trong ngành đó là gì? Công ty
đang tạo dựng lợi thế về chi phí hay lợi thế về
sự khác biệt để cạnh tranh trong môi trường
ngành như trên. Lập luận của Porter được rút ra
từ cách nhìn nhận, đặt ngành như là trung tâm
của sự chú ý chiến lược. Theo khuôn khổ của
Porter, đặc điểm cấu trúc của ngành của một
công ty mà nó đang hoạt động sẽ giải thích sự
thay đổi trong hoạt động doanh nghiệp. Một
công ty trong một ngành với các đối thủ cạnh
tranh ít, hàng nghìn nhà cung cấp cạnh tranh,
hàng triệu khách hàng háo hức, rào cản cao để
nhập ngành và khả năng không có sản phẩm
khác của công ty thay thế cho riêng của mình
đã thỏa mãn các yêu cầu cho một chiến lược
đầy hứa hẹn. Sau khi đã tìm thấy ngành có lợi
nhuận lớn để hoạt động thì nhiệm vụ tiếp theo
của tất cả công ty phải làm là chiếm ưu thế để
kiểm soát phần lớn lợi nhuận của ngành. Hay
nói một cách khác, một công ty thành công là
một công ty có khả năng độc quyền. Kết luận
hợp lý từ quan điểm này là chỉ có hai cách
cạnh tranh để tạo dựng độc quyền: thông qua
chi phí thấp hoặc khác biệt sản phẩm.
Từ quan điểm của Porter, chiến lược là
đánh bại các đối thủ cạnh tranh thông qua sự
cạnh tranh khốc liệt, chiến đấu với các khách
hàng và nhà cung cấp với khả năng thương
lượng và tạo ra những trở ngại cho người tham
gia mới.
Không giống M.Porter, Fjeldstad và
Stabell (1998) đã đưa ra một hệ tư tưởng mới
được gọi là “mạng giá trị” với quan điểm kinh
doanh là “chiến tranh và hòa bình” là “tranh
hợp”. Kinh doanh là sự hợp tác khi cần tạo ra
chiếc bánh nhưng sẽ là cạnh tranh khi đến lúc
chia phần chiếc bánh đó .
Theo mô hình mạng giá trị, 5 yếu tố cấu
thành cuộc chơi là Người chơi (Players), Giá
trị gia tăng (Added Values), Quy tắc (Rules),
Chiến thuật (Tactics) và Phạm vi (Scope) được
viết tắt theo tiếng Anh là PARTS. Cùng với
Mạng giá trị, các yếu tố này hợp thành một hệ
thống khái niệm cốt lõi để áp dụng lý thuyết
Trò chơi vào kinh doanh.
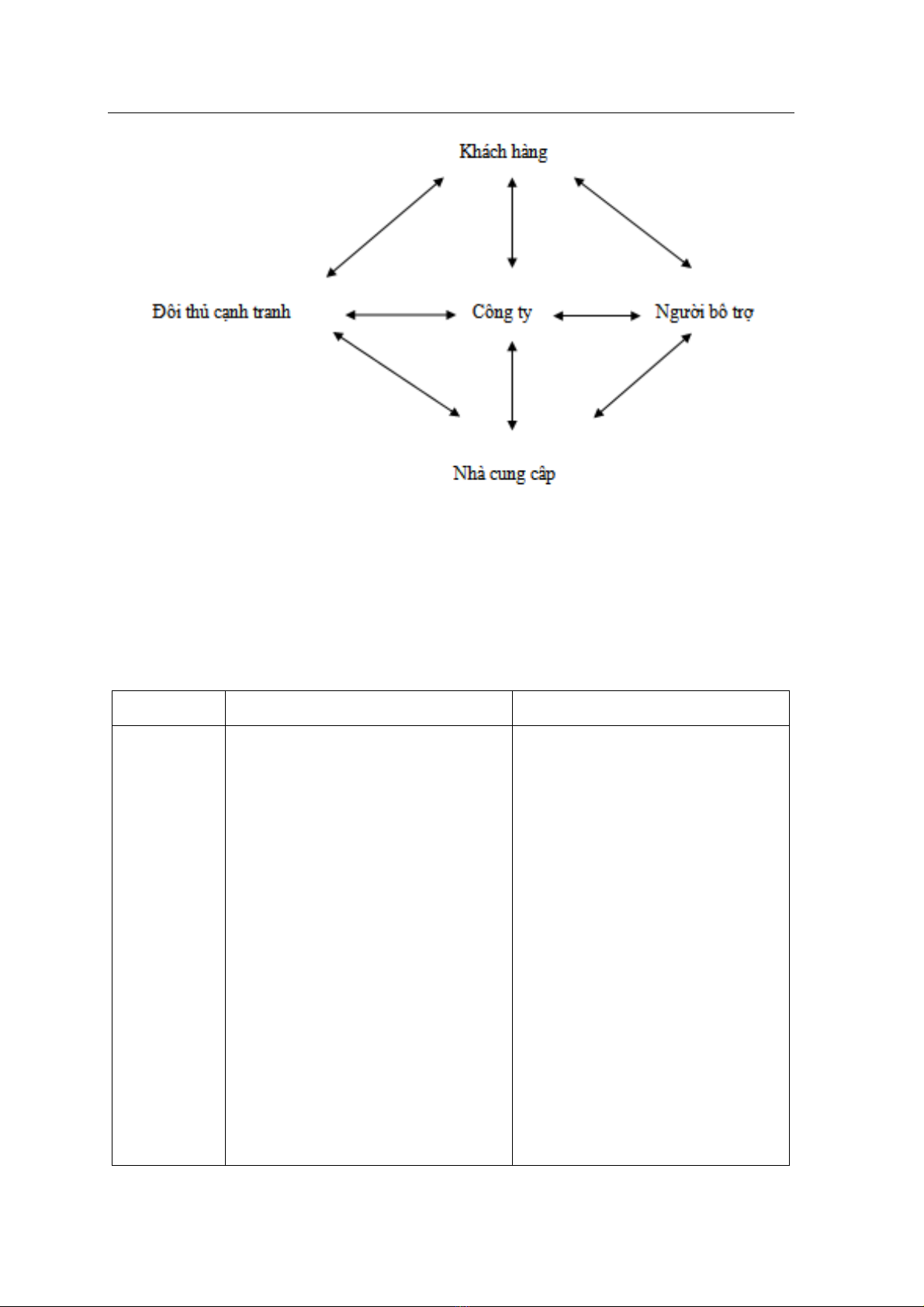
TRƯỜNG ĐẠI HỌC KINH TẾ - ĐẠI HỌC ĐÀ NẴNG
402
Sơ đồ 1.2.- Mạng giá trị
Bốn phía trong giản đồ Mạng giá trị, dù đó
là khách hàng, nhàcung cấp, người bổ trợ
(complementator), hay đối thủ cạnh tranh,
không ai có thể chỉ đóng một vai bạnhay thù. Ở
đây luôn có tính hai mang trong mỗi mối quan
hệ - đó là các thành tố đồngthời của hợp tác và
cạnh tranh. Chiến tranh và hòa bình. Tranh
hợp. Như vậy, luôn luôn tồn tại cả hai yếu tố
cùng thắng và thắng – thua trong các mối quan
hệ với: khách hàng, nhà cung cấp, đối thủ cạnh
tranh, nhà bổ trợ.
• Đánh giá và trường hợp ứng dụng của 2 mô hình:
Mô hình 5 lực lượng cạnh tranh Mạng giá trị
Ưu điểm
-Nhận biết mức độ cạnh tranh của các
nhân tố trong ngành và sức hấp dẫn
của ngành.
-Nhận biết được các cơ hội và đe dọa
mà doanh nghiệp phải đương đầu trong
ngành
- Quan điểm tranh hợp giúp cung cấp
một mô hình nhằm tổ chức những
thông tin có sẵn trên thị trường và
nhận biết những khe hở vì vậy mô
hình này trở nên rất có giá trị trong
việc lập kế hoạch chiến lược.
- Mô hình xây dựng dựa trên tư duy
hợp tác cũng quan trọng không kém
cạnh tranh, và một công ty có thể vừa
cạnh tranh vừa hợp tác với các công
ty khác cùng lúc.
- Trái ngược với Porter,Fjeldstad và
Stabell không đề cập đến khái niệm
về ngành mà xét về mối quan hệ tranh
hợp của từng công ty với các đối tác
của chúng. Qua đó nhận diện cơ hội
và đe dọa của từng công ty rõ ràng
hơn.

HỘI THẢO VỀ KHOA HỌC QUẢN TRỊ (CMS-2013)
403
Nhược điểm
- Chỉ trình bày về một bức tranh tĩnh
tại của ngành mà xem nhẹ về vai trò
của cải tiến . Cải tiến có thể làm thay
đổi cấu trúc ngành.
- Bỏ qua sự khác biệt của từng công ty.
Năng lực và nguồn lực của các công ty
là nhân tố quan trọng hơn nhiều so với
ngành trong việc xác định khả năng
sinh lợi.
- Mô hình này chỉ dựa trên suy nghĩ
cạnh tranh. Nó cho rằng các công ty
luôn cố gắng để giành lợi thế cạnh
tranh so với đối thủ, nhà cung cấp và
khách hàng. Mô hình đã bỏ qua những
chiến lược liên minh và hợp tác giữa
công ty và các nhân tố trong ngành từ
đó hạn chế những cơ hội kinh doanh
của công ty.
- Mô hình quá trừu tượng. Định nghĩa
về đối thủ cạnh tranh, nhà bổ trợ và
tranh hợp quá rộng.
-Mô hình này được xây dựng trên
nguyên tắc của lý thuyết trò chơi vì
vậy không thể tránh khỏi những hạn
chế của lý thuyết này. Ứng dụng lý
thuyết trò chơi sẽ trở nên phức tạp
hơn rất nhiều nếu nhiều người chơi
tham gia với nhiều sự lựa chọn được
thêm vào.
- Cạnh tranh và hợp tác thường xuất
hiện khi tiêu chuẩn ngành được thiết
lập, một quy trình mà Brandenburger
và Nalebuff không đề cập.
Áp dụng
Thường được áp dụng để phân tích các
ngành tĩnh tại, ít có sự biến đổi hoặc
dùng để phân tích một ngành chỉ tại
một thời điểm cụ thể.
Có thể áp dụng trong một môi trường
kinh doanh biến đổi liên tục và các
yếu tố trong môi trường có mối quan
hệ lẫn nhau.
2.2. Lý thuyết trò chơi :
Mạng giá trị đã cho chúng ta biết về những
người chơi và những mối quan hệ. Lý thuyết
trò chơi sẽ xác định kiểu, quy tắc chơi và cách
đưa ra quyết định.
Lý thuyết trò chơi khởi đầu là một nhánh
của ngành toán học ứng dụng. Cũng có thể gọi
đó là khoa học về chiến lược. Nó phân tích các
tình huống trong đó vận may của tất cả mọi
người đều phụ thuộc lẫn nhau. Lý thuyết trò
chơi đưa ra một cách thức có hệ thống để phát
triển các chiến lược khi số phận của người này
phụ thuộc vào những gì người khác làm.
Theo Robert Gibbons (1992) có thể phân
thành 4 loại trò chơi như sau :
Trong dạng trò chơi tĩnh với thông tin đầy
đủ, những người chơi đồng thời ra quyết định
(hay hành động) để tối ưu hóa kết quả (có thể
là lợi nhuận, v.v.); mỗi người chơi đều biết
rằng những người khác cũng đang cố gắng để
tối đa hóa kết quả mình sẽ thu được. Kết quả
cuối cùng cho mỗi người phụ thuộc vào phối
hợp hành động của họ.
Biểu diễn loại trò chơi này dưới dạng
chuẩn tắc (normal-form representation) với
minh họa Thế “lưỡng nan của người tù”
Poundstone, William (1992). Nếu trò chơi lặp
lại nhiều lần, người chơi cần có sự hợp tác nếu
không tổn thất sẽ rất lớn. Trò chơi động
(dynamic game) diễn ra trong nhiều giai đoạn,
và một số người chơi sẽ phải hành động ở mỗi

TRƯỜNG ĐẠI HỌC KINH TẾ - ĐẠI HỌC ĐÀ NẴNG
404
một giai đoạn. Để tìm điểm cân bằng cho các
trò động, chúng ta phải vận dụng phương pháp
quy nạp ngược (backward induction).
Hạn chế của lý thuyết trò chơi khi áp dụng
vào kinh doanh đó là phải xác định, giới hạn và
tính toán đầy đủ những yếu tố và biến số có thể
ảnh hưởng đến chiến lược và kết quả. Sẽ luôn
luôn có một nhân tố X nào đó không được tính
đến. Hạn chế thứ 2 đó là người chơi sẽ rất khó
biết được thưởng phạt của đối thủ, điều này
dẫn đến việc phân tích trở nên phức tạp hơn rất
nhiều. Ngoài ra, khi có nhiều người chơi tham
gia, ma trận thưởng phạt trở nên lớn hơn, việc
áp dụng lý thuyết trò chơi cũng rất phức tạp.
Một số trường hợp cạnh tranh cũng không thể
giải thích bằng lý thuyết trò chơi.
3. Trường hợp ứng dụng : Cuộc chiến bản
quyền giữa Apple và Samsung.
a) Người chơi
Apple và Samsung – 2 công ty hàng
đầu thế giới về điện thoại thông minh.
Hai
nhà sản xuất điện thoại di động lớn nhất thế
giới hiện vẫn đang “mắc kẹt” trong cuộc chiến
bản quyền tại ít nhất 10 quốc gia trên khắp thế
giới. Chúng ta sẽ dùng lý thuyết trò chơi để
xem xét một cách tổng thể tình huống này.
b) Thưởng phạt
Mỗi bên sẽ có 2 phương án : tấn công đối
thủ hoặc không làm gì cả (hoặc bị động). Như
vậy sẽ có tổng cộng 4 tình huống xảy ra.
• Nếu cả 2 đều không kiện nhau, 2 bên
đều không nhận được lợi thế nào so với đối
thủ.
• Nếu Apple hoặc Samsung tấn công
người kia:
- Người tấn công nếu thắng sẽ nhận
được tiền bồi thường từ người bị động đồng
thời gia tăng được thị phần. Nếu thua, bên tấn
công sẽ không gặp tổn thất quá lớn. Chẳng hạn
như năm 2012, Apple chỉ phải đăng lời xin lỗi
công khai với Apple sau khi đơn kiện của họ
tại Anh không được chấp thuận. Ngoài ra, bên
tấn công cũng sẽ mất một khoảng chi phí để
đầu tư vào vụ kiện, có thể lên đến hàng triệu đô
la. Nhìn chung, lợi thế của người tấn công là
rất đáng kể, để dễ so sánh chúng ta sẽ giả sử họ
được +10.
- Người bị động nếu thua đương nhiên
sẽ mất tiền để bồi thường cho bên kia. Ngoài ra
các sản phẩm của bên bị động còn bị cấm bán
nếu họ thất bại khiến giảm một lượng lớn
doanh thu. Vậy giả sử người bị động sẽ bị -10.
• Nếu cả 2 cùng lao vào cuộc chiến :
Việc cả 2 cùng lao vào cuộc chiến pháp lý, họ
sẽ tổn thất nhiều hơn là được lợi. Apple và
Samsung đã phải trả hàng triệu đô la cho các
luật sư trong mỗi lần kiện tụng của họ. Chiến
thắng dù có thuộc về bên nào đi nữa thì điều
này cũng sẽ ảnh hưởng đến các sản phẩm trong
tương lai.Bên cạnh đó, các đối thủ cạnh tranh
của Apple và Samsung sẽ được lợi. Tuy nhiên,
tổn thất của mỗi công ty sẽ giảm đi ít nhiều
nhờ vào tiền bồi thường họ nhận được từ bên
kia sau mỗi lần thắng kiện. Như vậy mỗi bên sẽ
bị -5 trong trường hợp này. Chúng ta có thể mô
tả trò chơi này giống như thế lưỡng nan của
người tù như sau:
c) Thảo luận về kết quả
Điểm cân bằng: Trong trường hợp này cả
Apple và Samsung đều có chiến lược áp đảo.
Bất kể hành động nào của đối phương, tấn
công đối thủ luôn là giải pháp tốt nhất cho cả
Apple và Samsung. Cụ thể, nếu như Apple tấn
công, Samsung tốt nhất nên tấn công lại Apple
khi đó họ sẽ tổn thất ít hơn khi bị động ( -5 so
với -10 ). Khi Apple bị động, phương án tấn
công vẫn là tốt nhất cho Samsung vì họ sẽ
được +10 so với 0 khi Samsung cũng không
làm gì cả. Những điều trên cũng đúng với
Apple. Như vậy điểm cân bằng Nash ở đây
chính là khi cả 2 bên đều tấn công đối thủ. Như
đã đề cập ở phần trên, cân bằng Nash có tính





![Bài giảng Trò chơi lưu động [chuẩn SEO]](https://cdn.tailieu.vn/images/document/thumbnail/2014/20140417/next_12/135x160/4361397726845.jpg)




















