Chương trình Giảng dạy Kinh tế Fulbright Kinh tế vi moâ Nhaäp moân Lyù thuyeát troø chôi
Nieân khoùa 2004 – 2005 Phaàn 1
GIÔÙI THIEÄU LYÙ THUYEÁT TROØ CHÔI
VAØ MOÄT SOÁ ÖÙNG DUÏNG TRONG KINH TEÁ HOÏC VI MOÂ
Cho ñeán nay, chuùng ta ñaõ nghieân cöùu boán hình thaùi caáu truùc thò tröôøng cô baûn laø caïnh
tranh hoaøn haûo, ñoäc quyeàn, caïnh tranh ñoäc quyeàn, vaø ñoäc quyeàn nhoùm. Nguyeân taéc toái
ña hoùa lôïi nhuaän cuûa caùc doanh nghiệp hoaït ñoäng treân 3 loaïi thị trường ñaàu laø quy taéc
quen thuoäc MR = MC. Trong khi ñoù, ôû thị trường ñoäc quyeàn nhoùm (oligopoly), moãi
doanh nghieäp treân thị trường coù moät theá löïc nhaát ñònh, ñoàng thôøi toàn taïi töông taùc
chieán löôïc (veà ñònh giaù vaø saûn löôïng chaúng haïn) vôùi nhöõng doanh nghiệp khaùc thì
coâng thöùc MR = MC khoâng coøn thích hôïp nöõa. Vì vaäy, ñeå nghieân cöùu öùng xöû cuûa caùc
doanh nghiệp trong loaïi hình caáu truùc thị trường naøy, chuùng ta phaûi sử dụng moät coâng
cuï coù khaû naêng phaân tích ñöôïc nhöõng töông taùc chieán löôïc cuûa caùc doanh nghiệp tham
gia thị trường. Coâng cuï ñoù laø lyù thuyeát troø chôi.1 Lyù thuyeát troø chôi nghieân cöùu caùc tình
huoáng ra quyeát ñònh coù lieân quan tôùi nhieàu ngöôøi vaø caùc quyeát ñònh cuûa moãi ngöôøi aûnh
höôûng tôùi lôïi ích vaø quyeát ñònh cuûa nhöõng ngöôøi khaùc.
Coù moät soá phöông phaùp phaân loaïi troø chôi. Neáu caên cöù vaøo khaû naêng hôïp ñoàng vaø cheá
taøi hôïp ñoàng cuûa nhöõng ngöôøi chôi thì coù theå chia troø chôi thaønh hai loaïi: troø chôi hôïp
taùc (cooperative games) vaø troø chôi baát hôïp taùc (non-cooperative games). Trong troø
chôi hôïp taùc, nhöõng ngöôøi chôi coù khaû naêng cuøng nhau laäp chöông trình (keá hoaïch)
haønh ñoäng töø tröôùc, ñoàng thôøi coù khaû naêng cheá taøi nhöõng thoûa thuaän chung naøy. Coøn
trong troø chôi baát hôïp taùc, nhöõng ngöôøi chôi khoâng theå tieán tôùi moät hôïp ñoàng (kheá
öôùc) tröôùc khi haønh ñoäng, hoaëc neáu coù theå coù hôïp ñoàng thì nhöõng hôïp ñoàng naøy khoù
ñöôïc cheá taøi.
Phöông phaùp phaân loaïi troø chôi thöù hai laø caên cöù vaøo thoâng tin vaø vaøo thôøi gian haønh
ñoäng cuûa nhöõng ngöôøi chôi. Caên cöù vaøo thoâng tin thì caùc troø chôi coù theå chia thaønh troø
chôi vôùi thoâng tin ñaày ñuû (complete information) hoaëc khoâng ñaày ñuû (incomplete
information). Troø chôi vôùi thoâng tin ñaày ñuû laø troø chôi maø moãi ngöôøi chôi coù theå tính
toaùn ñöôïc keát quaû (payoff) cuûa taát caû nhöõng ngöôøi coøn laïi. Caên cöù vaøo thôøi gian haønh
ñoäng laïi coù theå chia troø chôi thaønh hai loaïi, tónh vaø ñoäng. Trong troø chôi tónh (static
game), nhöõng ngöôøi chôi haønh ñoäng ñoàng thôøi, vaø keát quaû cuoái cuøng cuûa moãi ngöôøi
phuï thuoäc vaøo phoái hôïp haønh ñoäng cuûa taát caû moïi ngöôøi. Troø chôi ñoäng (dynamic
game) dieãn ra trong nhieàu giai ñoaïn, vaø moät soá ngöôøi chôi seõ haønh ñoäng ôû moãi moät
giai ñoaïn.2 Phoái hôïp hai tieâu thöùc phaân loaïi naøy ta seõ coù boán heä troø chôi töông öùng vôùi
1 Lyù thuyeát troø chôi töø laâu ñaõ trôû thaønh moät lónh vöïc quan troïng cuûa kinh teá hoïc noùi chung. Noù coù öùng
duïng roäng raõi trong kinh teá hoïc vi moâ, vó moâ, taøi chính, quaûn trò, ngaân haøng, thöông maïi quoác teá, chính
trò, khoa hoïc veà chieán tranh, ngoaïi giao … noùi chung laø trong caùc moâi tröôøng coù töông taùc chieán löôïc.
2 Neáu moãi ngöôøi chôi ôû thôøi ñieåm phaûi ra quyeát ñònh maø bieát toaøn toaøn lòch söû cuûa troø chôi cho ñeán thôøi
ñieåm ñoù thì ta noùi raèng troø chôi naøy coù thoâng tin hoaøn haûo (perfect information), baèng khoâng chuùng ta
noùi raèng troø chôi coù thoâng tin khoâng hoaøn haûo (imperfect information).
Vũ Thaønh Tự Anh
1
Chương trình Giảng dạy Kinh tế Fulbright Kinh tế vi moâ Nhaäp moân Lyù thuyeát troø chôi
Nieân khoùa 2004 – 2005 Phaàn 1
boán khaùi nieäm veà ñieåm caân baèng, trong ñoù khaùi nieäm caân baèng sau maïnh hôn khaùi
nieäm caân baèng tröôùc theo chieàu muõi teân (xem Baûng 1).
Tónh Ñoäng
Thoâng tin ñaày ñuû Caân baèng Nash – NE Subgame Perfect Nash Equilibrium -SPNS
Thoâng tin khoâng ñaày ñuû Bayesian Nash Equilibrium - BNE Perfect Bayesian Equilibrium - PBE
Baûng 1: Boán heä troø chôi vaø caùc khaùi nieäm caân baèng töông öùng
Phaàn 1: Troø chôi ñoäng vôùi thoâng tin ñaày ñuû
Daïng thöùc cuûa troø chôi naøy laø nhöõng ngöôøi chôi ñoàng thôøi ra quyeát ñònh (hay haønh
ñoäng) ñeå toái öu hoùa keát quaû (coù theå laø ñoä thoûa duïng, lôïi nhuaän, v.v.); ñoàng thôøi moãi
ngöôøi chôi ñeàu bieát raèng nhöõng ngöôøi khaùc cuõng ñang coá gaéng ñeå toái ña hoùa keát quaû
mình seõ thu ñöôïc. Keát quaû cuoái cuøng cho moãi ngöôøi phuï thuoäc vaøo phoái hôïp haønh
ñoäng cuûa hoï.
Bieåu dieãn troø chôi döôùi daïng chuaån taéc (normal-form representation)
Ví duï 1: Theá “löôõng nan cuûa ngöôøi tuø”
Giaû söû Giaùp vaø Aát bò tình nghi cuøng nhau aên caép. Hai ngöôøi bò coâng an baét veà ñoàn
nhöng chöa theå keát toäi neáu caû Giaùp vaø Aát cuøng khoâng nhaän toäi. Coâng an môùi nghó ra
moät caùch nhö sau khieán Giaùp vaø Aát phaûi cung khai ñuùng söï thaät. Coâng an seõ giam
Giaùp vaø Aát vaøo hai phoøng taùch bieät, khoâng cho pheùp hoï ñöôïc thoâng tin cho nhau vaø
thoâng baùo vôùi moãi ngöôøi raèng: Neáu caû hai cuøng khoâng chòuï khai mình phaïm toäi thì
moãi ngöôøi seõ bò giöõ theâm 1 thaùng ñeå thaåm tra vaø tìm theâm chöùng cöù. Neáu caû hai cuøng
khai nhaän toäi thì moãi ngöôøi seõ phaûi ngoài tuø 4 thaùng. Neáu chæ coù moät ngöôøi nhaän toäi coøn
ngöôøi kia ngoan coá khoâng chòu nhaän toäi thì ngöôøi thaønh khaån cung khai seõ ñöôïc höôûng
söï khoan hoàng vaø khoâng phaûi ngoài tuø, trong khi ngöôøi kia seõ chòu hình phaït naëng hôn
laø 5 thaùng tuø giam. Caùc khaû naêng vaø keát cuïc naøy ñöôïc trình baøy moät caùch chuaån taéc
trong Baûng 2 döôùi ñaây.3
3 Moät caùch khaùc, daïng chuaån taéc cuûa troø chôi tónh vôùi thoâng tin ñaày ñuû coù theå ñöôïc bieåu dieãn döôùi daïng
G = {S1, S2, …, Sn; u1, u2, …, un} trong ñoù chuùng ta coù theå ñoïc ñöôïc caùc thoâng tin veà soá ngöôøi chôi (n),
khoâng gian chieán löôïc (hay caùc chieán löôïc coù theå - Si), vaø caùc keát cuïc (payoff) töông öùng (ui).
Vũ Thaønh Tự Anh
2
Chương trình Giảng dạy Kinh tế Fulbright Kinh tế vi moâ Nhaäp moân Lyù thuyeát troø chôi
Nieân khoùa 2004 – 2005 Phaàn 1
Giaùp
Khai Khoâng khai
Khai -4, -4 0, -5
AÁt Khoâng khai -5, 0 -1, -1
Baûng 2: Theá löôõng nan cuûa ngöôøi tuø
Chieán löôïc aùp ñaûo (dominant strategy) vaø chieán löôïc bò aùp ñaûo (dominated strategy)
Trong cuoäc chôi naøy, Giaùp vaø Aát moãi ngöôøi chæ coù theå löïa choïn moät trong hai chieán
löôïc (haønh ñoäng): Khai hoaëc khoâng khai. Giaùp coù theå tö duy theá naøy. “Neáu thaèng Aát
nhaän toäi maø mình laïi khoâng nhaän toäi thì noù traéng aùn coøn mình phaûi ngoài boùc lòch
nhöõng 5 thaùng. Nhö theá thì thaø mình cuõng nhaän toäi ñeå chæ phaûi ngoài tuø 4 thaùng coøn
hôn”. Roài Giaùp laïi nghó, “nhöng ngoä nhôõ thaèng Aát noù ngoan cöôøng khoâng khai thì
mình neân theá naøo nhæ? Neáu noù khoâng khai maø mình cuõng khoâng khai thì mình phaûi
ngoài tuø 1 thaùng, nhöng maø neáu mình khai thì mình coøn ñöôïc tha boång cô maø. Nhö vaäy
toát nhaát laø maëc keä thaèng Aát, mình cöù khai baùo laø hôn.” Nhö vaäy, duø Aát coù löïa choïn theá
naøo thì phöông aùn toát nhaát ñoái vôùi Giaùp laø khai nhaän toäi. Töông töï nhö vaäy, duø Aát coù
löïa choïn theá naøo thì phöông aùn toát nhaát ñoái vôùi Giaùp laø khai nhaän toäi. Noùi caùch khaùc,
ñoái vôùi caû Giaùp vaø Aát thì chieán löôïc “khai nhaän toäi” laø chieán löôïc aùp ñaûo so vôùi chieán
löôïc “khoâng khai”; ngöôïc laïi, chieán löôïc “khoâng khai” laø chieán löôïc bò aùp ñaûo so vôùi
chieán löôïc “khai nhaän toäi.”
Trong ví duï naøy moãi ngöôøi chôi chæ coù hai chieán löôïc löïa choïn, vaø vì vaäy chieán löôïc aùp
ñaûo cuõng ñoàng thôøi laø chieán löôïc toát nhaát. Trong nhöõng baøi toaùn coù nhieàu ngöôøi chôi
vôùi khoâng gian chieán löôïc lôùn hôn thì ñeå tìm ra ñieåm caân baèng cuûa troø chôi, chuùng ta
phaûi laàn löôït loaïi tröø taát caû caùc chieán löôïc bò aùp ñaûo. Tuy nhieân ñoái vôùi caùc troø chôi
phöùc taïp ñieàu naøy khoâng ñôn giaûn, vaø thaäm chí ngay caû khi loaïi heát caùc chieán löôïc bò
aùp ñaûo roài chuùng ta vaãn chöa theå tìm ñöôïc ñieåm caân baèng. Trong ví duï trình baøy ôû
Baûng 3, coù hai ngöôøi chôi, moãi ngöôøi coù 3 löïa choïn. Sau khi loaïi heát caùc chieán löôïc bò
aùp ñaûo chuùng ta vaãn chöa theå tìm ñöôïc ñieåm caân baèng. Xuaát phaùt töø haïn cheá naøy cuûa
phöông phaùp loaïi tröø caùc chieán löôïc bò aùp ñaûo, Nash ñaõ ñöa ra moät khaùi nieäm caân
baèng maïnh hôn.
Traùi Giöõa Phaûi
Traùi 0, 4 4, 0 5, 3
Giöõa 4, 0 0, 4 5, 3
Phaûi 3, 5 3, 5 6, 6
Baûng 3: Loaïi tröø caùc chieán löôïc bò aùp ñaûo vaø caân baèng Nash
Vũ Thaønh Tự Anh
3
Chương trình Giảng dạy Kinh tế Fulbright Kinh tế vi moâ Nhaäp moân Lyù thuyeát troø chôi
Nieân khoùa 2004 – 2005 Phaàn 1
Trong ví duï ôû Baûng 3, caân baèng Nash duy nhaát laø (phaûi, phaûi) vôùi keát cuïc laø (6,6)
nhöng neáu chæ duøng phöông phaùp loaïi tröø caùc chieán löôïc bò aùp ñaûo thì khoâng theå keát
luaän ñöôïc ñaâu laø ñieåm caân baèng.
Caân baèng Nash: Trong troø chôi daïng chuaån taéc G = {S1, S2, …, Sn; u1, u2, …, un}, toå hôïp
chieán löôïc (s*1, s*2, …, s*n) laø moät caân baèng Nash neáu, vôùi moãi moät ngöôøi chôi i naøo ñoù,
s*i (töùc laø chieán löôïc do ngöôøi thöù i löïa choïn) laø phaûn öùng toát nhaát cuûa ngöôøi chôi naøy
ñoái vôùi caùc chieán löôïc cuûa (n-1) ngöôøi chôi coøn laïi (s*1, s*2, …, s*i-1, s*i+1, …, s*n) (kyù
hieäu laø s*-i). Noùi caùch khaùc, ui(s*i, s*-i) ≥ ui(si, s*-i).
Veà maët toaùn hoïc, s*i laø nghieäm cuûa baøi toaùn toái öu:
*
max ( , )
ii i
ii
uss
sS −
∈
Trong ví duï cuûa Giaùp vaø AÁt, ñieåm caân baèng cuûa troø chôi laø (“khai”, “khai”) trong ñoù
Giaùp vaø AÁt cuøng khai nhaän toäi, vaø ñaây cuõng laø caân baèng Nash duy nhaát cuûa troø chôi
naøy.
Löu yù raèng vì caân baèng Nash ñöôïc taïo bôûi nhöõng chieán löôïc phaûn öùng toái cuûa taát caû
ngöôøi chôi (öùng vôùi caùc chieán löôïc toái öu cuûa nhöõng ngöôøi chôi coøn laïi) neân noù coù tính
oån ñònh vaø beàn vöõng veà maët chieán löôïc (strategically stable), ñoàng thôøi noù coù tính chaát
töï cheá taøi (self-enforcement) – töùc laø moãi ngöôøi chôi, khi cöïc ñaïi hoùa lôïi ích cuûa mình,
seõ töï nguyeän tuaân thuû caân baèng Nash, ñoàng thôøi hoï khoâng heà coù ñoäng cô ñeå di chuyeån
khoûi ñieåm caân baèng naøy.
Sau khi döï baùo ñöôïc öùng xöû cuûa nhöõng ngöôøi chôi khaùc thì moãi ngöôøi chôi choïn chieán
löôïc (quyeát ñònh) ñeå toái öu hoùa lôïi ích cuûa mình. Chieán löôïc (quyeát ñònh) naøy vì vaäy
ñöôïc goïi laø phaûn öùng toát nhaát (best response). Quay lai baøi toaùn cuûa 2 ngöôøi tuø, nhö ñaõ
laäp luaän ôû phaàn treân, “nhaän toäi” laø phaûn öùng toát nhaát cuûa caû Giaùp vaø Aát, vaø phaûn öùng
toát nhaát naøy khoâng phuï thuoäc vaøo haønh ñoäng cuï theå cuûa ngöôøi kia (nhôù laïi raèng “nhaän
toäi” laø chieán löôïc aùp ñaûo)
Moät soá öùng duïng cuûa troø chôi tónh vôùi thoâng tin ñaày ñuû
ÖÙng duïng 1: Ñoäc quyeàn song phöông Cournot (1838)
Giaû söû coù 2 coâng ty hoaït ñoäng trong thị trường ñoäc quyeàn song phöông theo kieåu
Cournot vaø cuøng saûn xuaát moät sản phẩm ñoàng nhaát. Saûn löôïng cuûa hai haõng laàn löôït laø
q1 vaø q2. Toång cung cuûa thị trường vì vaäy laø Q = q1 + q2. Ñeå ñôn giaûn, giaû söû haøm caàu
coù daïng tuyeán tính: P(Q) = a – Q = a – (q1 + q2). Cuoái cuøng, giaû söû raèng chi phí caän
bieân vaø chi phí trung bình cuûa caû 2 haõng baèng nhau vaø baèng haèng soá c, töùc laø: Ci(qi) =
c.qi , trong ñoù c < a.
Baøi toaùn cuûa moãi haõng laø choïn saûn löôïng ñeå toái ña hoùa lôïi nhuaän
• Baøi toaùn daïng chuaån taéc:
i) Soá ngöôøi chôi: 2
Vũ Thaønh Tự Anh
4
Chương trình Giảng dạy Kinh tế Fulbright Kinh tế vi moâ Nhaäp moân Lyù thuyeát troø chôi
Nieân khoùa 2004 – 2005 Phaàn 1
ii) Khoâng gian chieán löôïc: Si = [0, a]
iii) Keát quaû
Π1(q1, q2) = q1[P(Q) – c ] = q1 [ a – (q1 + q2) -c]
Π2(q1, q2) = q2[P(Q) – c ] = q2 [ a – (q1 + q2) -c]
• Ñònh nghóa caân baèng Nash:
Caëp (s1*, s2*) laø caân baèng Nash Ù u1(s1*, s2*) ≥ u1(s1, s2*) vaø
u2(s1*, s2*) ≥ u2(s1*, s2)
Ù = Π(q
11
*
211 ),(max
Ss
ssu
∈1, q2) = q1[a –(q1 + q2*) -c] => q1 = 2
*
2
qca −− 3
*
2
*
1
ca
qq
−
==
22
2
*
12 ),(max
Ss
ssu
∈ = Π(q1, q2) = q2[a–(q1* + q2) -c] => q2 = 2
*
1
qca −−
vaø 9
)( 2
*
2
*
1
ca −
=Π=Π
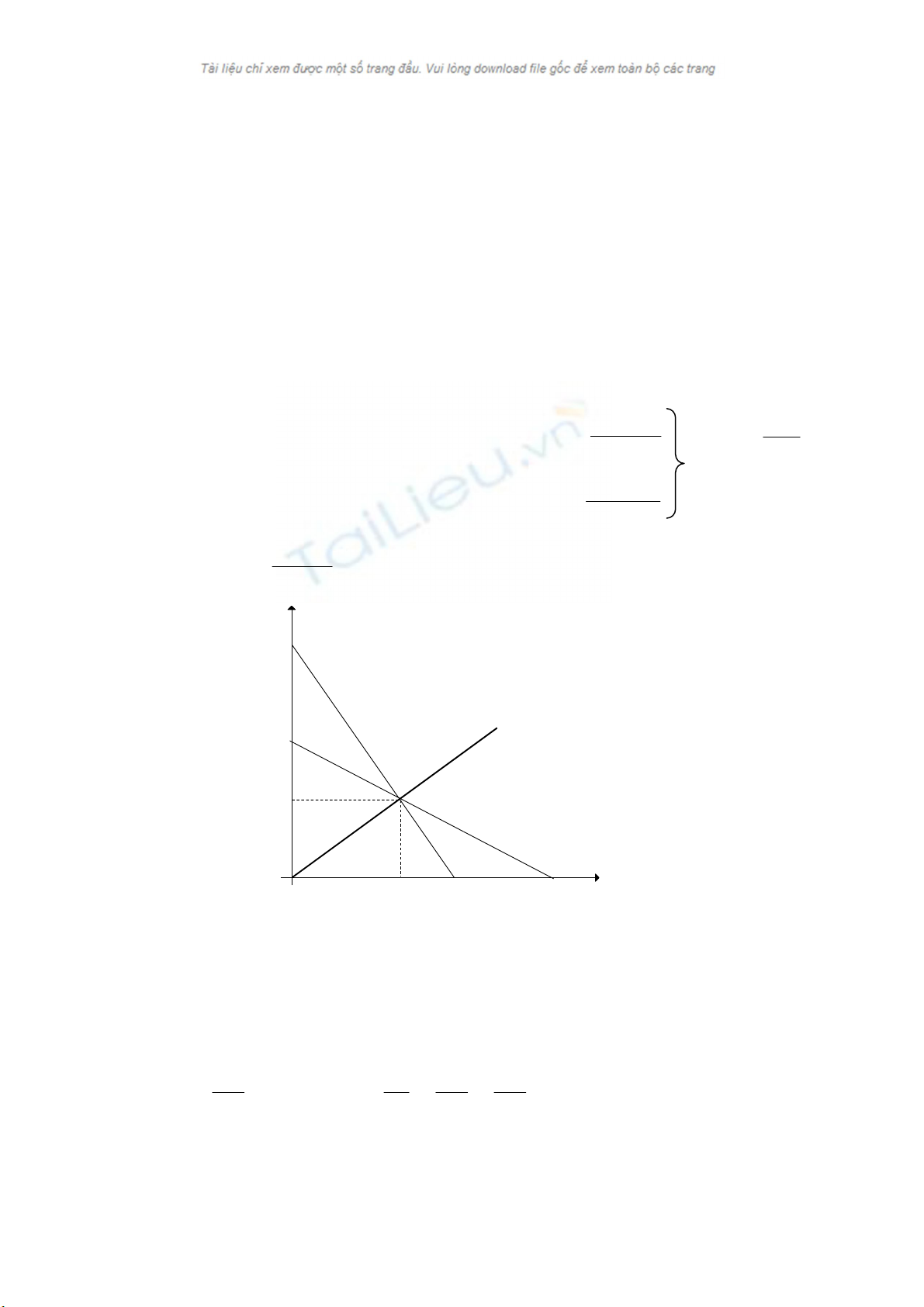
(a-c)
(a-c)/2
(a-c)/3
q2
q1
(a-c)/3 (a-c) (a-c)/2
Hình 1: Caân baèng Nash cuûa caïnh tranh ñoäc quyeàn song phöông Cournot
Baây giôø xem xeùt tröôøng hôïp 2 coâng ty caáu keát vôùi nhau vaø hoaït ñoäng nhö 1 coâng ty
ñoäc quyeàn. Khi aáy, chuùng phaûi giaûi choïn Q sao cho:
[0, ]
[() ] [ ]
m
Qa
M
ax Q P Q c Q a Q c
∈Π= − = − −
→
12
*
*** *
1
2243
m
mmm
Q
ac ac ac
Qqq q
−−−
=⇒===<==
*
2
q
, trong ñoù giaû söû raèng hai
haõng chia ñoâi saûn löôïng.
Vũ Thaønh Tự Anh
5