
1
Chương 3:
MẬT ĐỘ ĐIỆN THÔNG,
ĐỊNH LUẬT GAUSS,
VÀ ĐỊNH LÝ DIVERGENCE
16/01/2013 CHÂU VĂN BẢO-ĐHCN TP.HCM
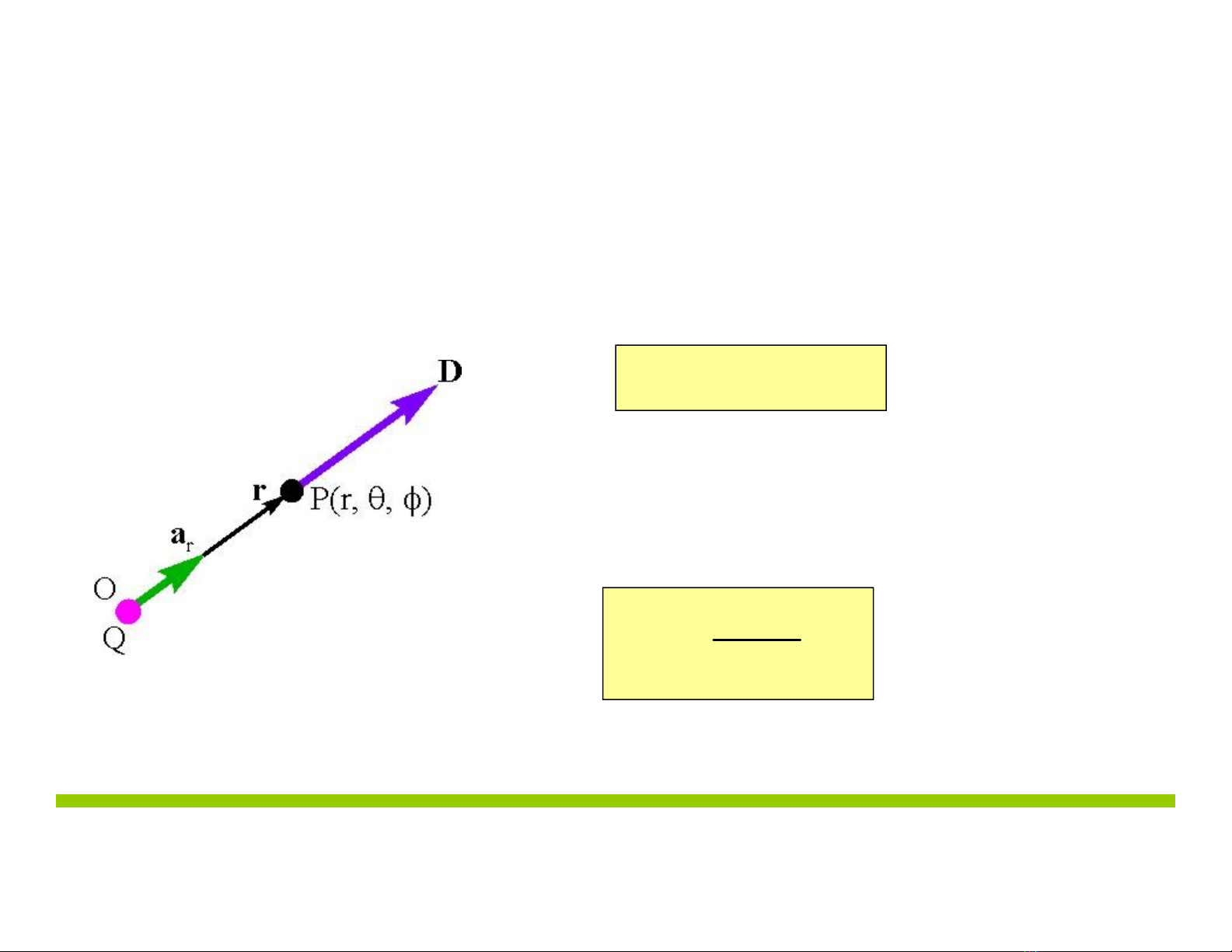
1. Định nghĩa: D (C/m2)
MậtđộđiệnthôngDdo điệntíchQtạoratạiPlà1vectơcóchiều
củađiệntrườngEvàcó độ lớnbằngmậtđộđiệntích ρstạiP.
(2)
3.1. MẬT ĐỘ ĐIỆN THÔNG
D= εoE(C/m2)
2.Mậtđộđiệnthôngcủađiệntích
tại1điểm(FigC3.1)
Tronghệtọađộ cầu
2
4
=
r
Q
r
π
Da
(1)
Figure C3 .1
16/01/2013 CHÂU VĂN BẢO-ĐHCN TP.HCM 2
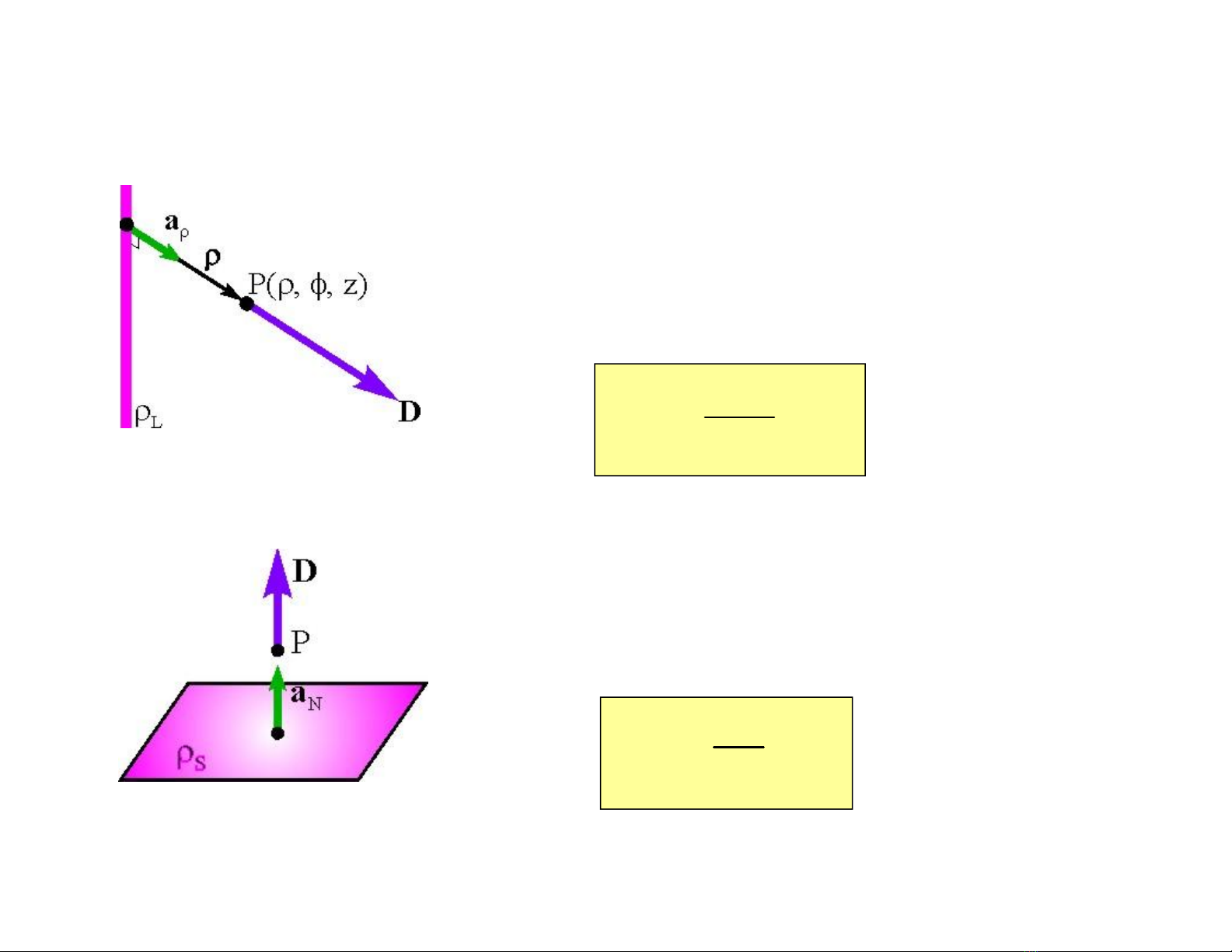
3.1. MẬT ĐỘ ĐIỆN THÔNG
3. Mật độ điện thông của điện tích phân bố theo đường (Fig C3.2)
2
=L
ρ
ρ
πρ
Da
(C1)
4. Mật độ điện thông xuyên qua mặt phẳng S (Fig C3.3)
TRonghệtọađộ trụ(CCS)dọctheotrụcz
ρ
L
:làmậtđộđiệntích
ρS:Làmậtđộđiệntíchmặt
N
2
=S
ρ
Da
(C2)
Figure C3 .2
Figure C3 .3
16/01/2013 CHÂU VĂN BẢO-ĐHCN TP.HCM 3
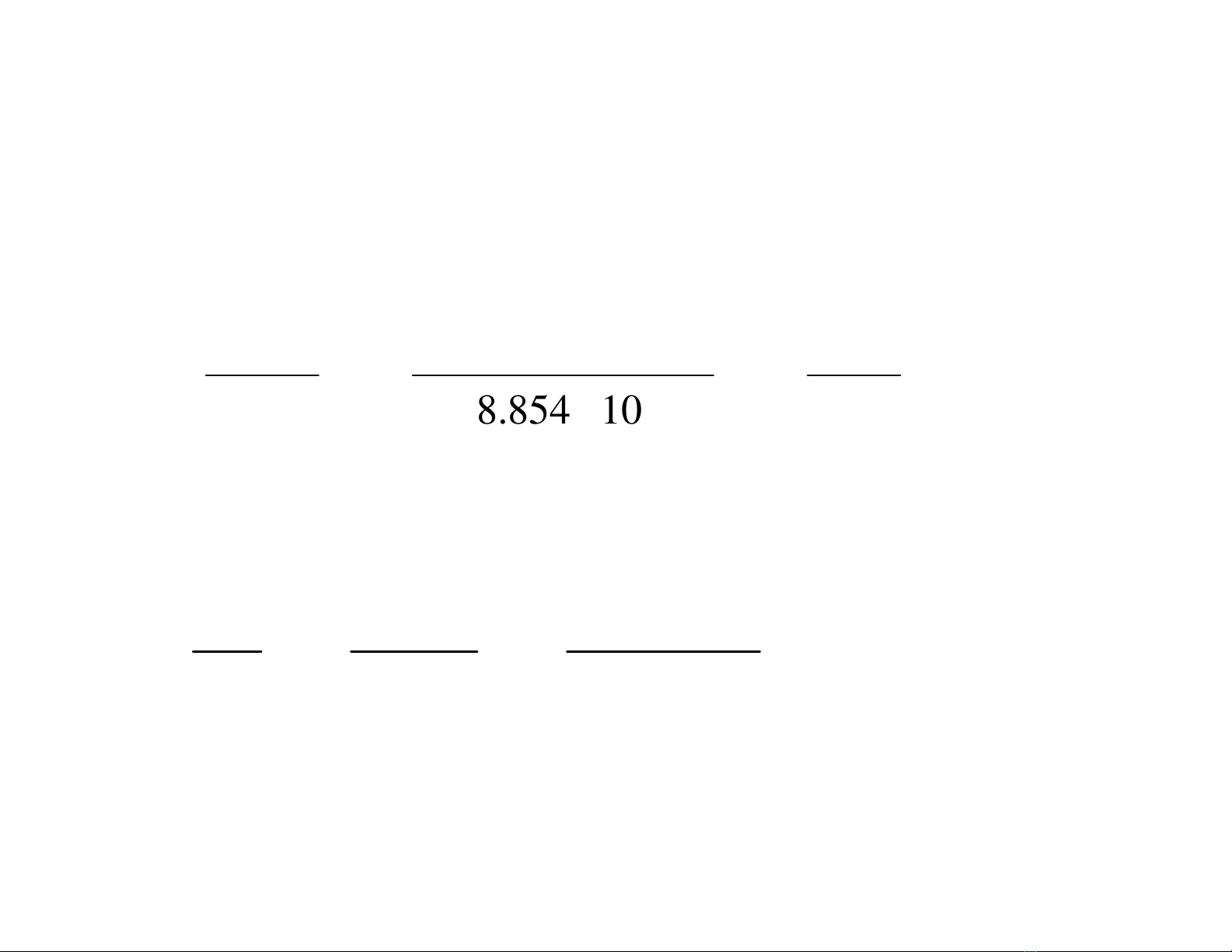
VD3.1. Điệntíchphânbốđềuvớimậtđộρ
L=8nC/mdọctheo
trụcz.Tìm Evà DtạiđiểmPcáchtrụczkhoảng3m.
Giải. Điện trường Etại P (ρ, φ, z) là
9
12
810143.8
(V/m)
22(8.85410)
−
−
×
===
×
L
o
ρρρ
ρ
περρ
π
Eaaa
Tạiρ=3m, E=47.9 aρ(V/m)
Thôngqua E,tatìm D
99
2
8101.27310
(C/m)
22
−−
××
===
L
ρρρ
ρ
πρπρρ
Daaa
Tạiρ=3mthì D=0.424aρ(nC/m2)
3.1. MẬT ĐỘ ĐIỆN THÔNG
16/01/2013 CHÂU VĂN BẢO-ĐHCN TP.HCM 4

DRILLPROBLEM3.1. Givena90 µCpointchargelocatedat
theorigin,findthetotalelectricfluxpassingthrough:
(a)thatportionofthespherer=26cmboundedby0<θ<π/2and
0<φ<π/2;(b)theclosedsurfacedefinedby ρ=26cmand
z=±26cm;(c)theplanez=26cm.
ANSWERS. (a)7.5(µC);(b)60(µC);(c)30(µC)
DRILLPROBLEM3.2. Calculate Dinrectangularcoordinates
atpointP(2,–3,6)producedby:(a)apointchargeQ
A=55mCat
PA(–2,3,–6);(b)auniformlinecharge ρSB =20mC/monthe
xaxis;(c)auniformsurfacecharge ρSC =120µC/m2ontheplane
z=–5m.
ANSWERS: (a) 6.38 ax –9.57 ay+ 19.14az(µC/m2);
(b) –212 ay+ 424 az(µC/m2); (c) 60az(µC/m2)
3.1. Electric Flux Density
16/01/2013 CHÂU VĂN BẢO-ĐHCN TP.HCM 5


























