Bài giảng Vật lý đại cương 1 - Chương 3: Động lực học hệ chất điểm

Chia sẻ: Hứa Tung | Ngày: | Loại File: PDF | Số trang:92

Thêm vào BST

Báo xấu

70
lượt xem 6
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng Vật lý đại cương 1 - Chương 3: Động lực học hệ chất điểm cung cấp cho người học các kiến thức về: động lượng hệ chất điểm, khối tâm, mômen động lực học chất điểm, mômen quán tính, động năng của hệ chất điểm,... Mời các bạn cùng tham khảo chi tiết nội dung bài giảng.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Vật lý đại cương 1 - Chương 3: Động lực học hệ chất điểm

Chương III ĐỘNG LỰC HỌC HỆ CHẤT ĐiỂM
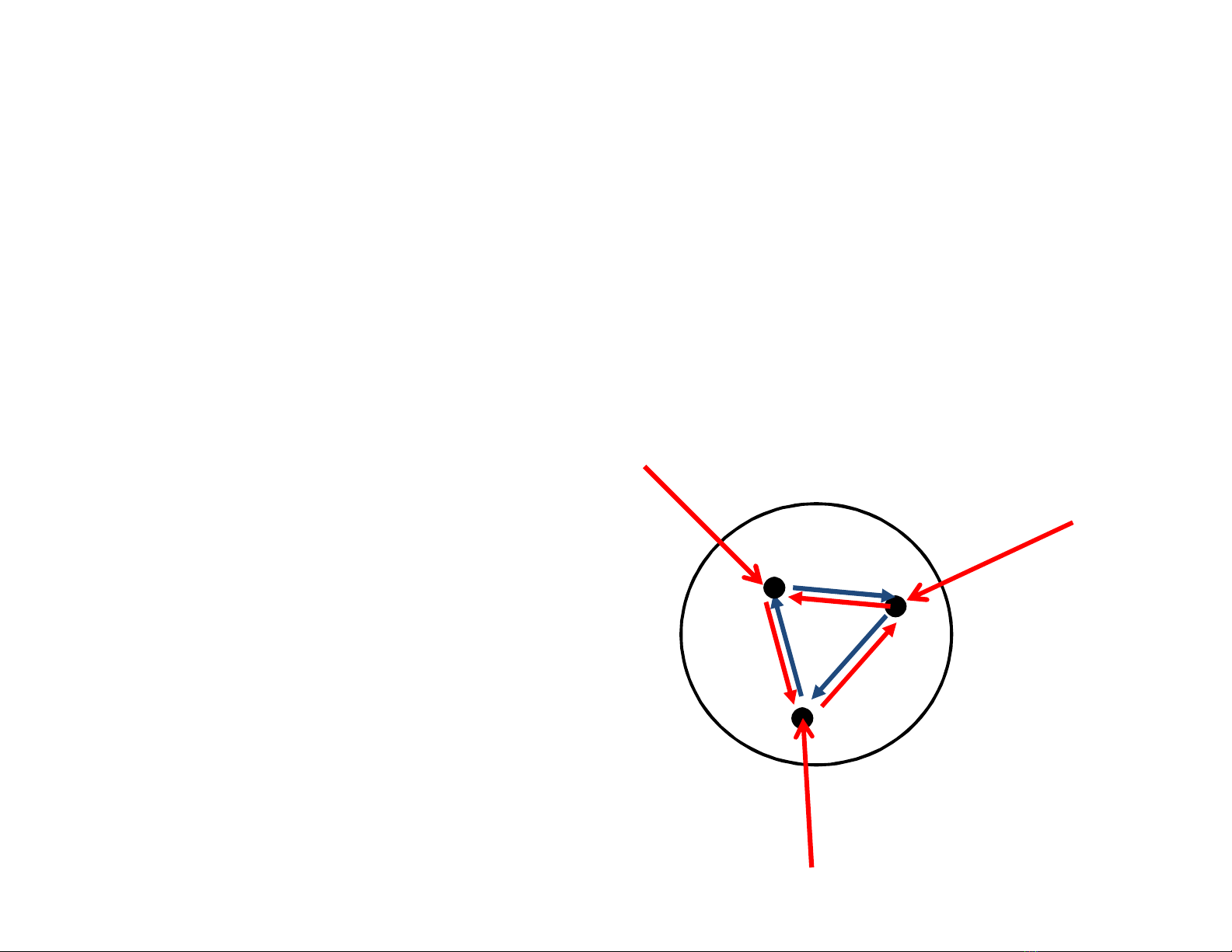
Nội lực là lực do các phần tử bên trong hệ tác dụng lên nhau. Ngoại lực là lực bên ngoài hệ tác dụng lên các phần tử bên trong hệ. Theo ĐL Newton III thì tổng các nội lực bằng không. Từ đó suy ra tổng momen của các nội lực cũng bằng không. 1 2 3
I. Động lượng hệ chất điểm 1. Định nghĩa: P   pi   mi vi i i 2. Định lý và định luật ĐLHCĐ    a) dP d pi d pi  ,  ;  Fi  Fi dt i dt dt Fi là tổng các ngoại lực tác dụng vào chất điểm i F’i là tổng các nội lực tác dụng vào chất điểm i  dP        Fi   Fi ,   Fi  F dt i i i
• Vậy:  d P  F dt   F   Fi là tổng các ngoại lực tác dụng vào HCĐ i b) p2 t2 t2  d P   F dt  P2  P1   F dt p1 t1 t1   c) Nếu F  0  p  const
  d) Nếu F  0 nhưng hình chiếu của F lên một phương nào đó bằng không thì động lượng được bảo toàn theo phương đó . Ví dụ: Fx = 0 thì Px = const Ví dụ: Một khẩu đại bác không có bộ phận chống giật, nhả đạn dưới một góc α = 45o so với mặt phẳng nằm ngang. Viên đạn có khối lượng m = 10kg và có vận tốc ban đầu vo = 200m/s. Đại bác có khối lượng M = 500kg. Hỏi vận tốc giật lùi của súng nếu bỏ qua ma sát
Giải: Ngoại lực tác dụng lên hệ gồm trọng lực và phản lực của mặt đường có phương thẳng đứng. Nên hình chiếu của chúng lên phương ngang bằng không Áp dụng ĐLBTĐL theo phương ngang cho hệ gồm súng và đạn mv cos   MV  0 mv cos  V    3,5m / s M
Một người có khối lượng m = 60kg đứng trên một con thuyền dài 3m có khối lượng M = 120kg, đang đứng yên trên mặt nước yên lặng. Người đó bắt đầu đi từ mũi thuyền đến chỗ lái thuyền (đuôi thuyền). Hỏi khi người đó đi tới chỗ lái thuyền thì thuyền đã đi được một đoạn bao nhiêu? Bỏ qua sức cản của nước.
Áp dụng ĐLBTĐL cho hệ người và thuyền:    m  0  mv1  M v2  v2   v1  M v1 là vận tốc của người đối với bờ  v 2 là vận tốc của thuyền đối với bờ  ' Gọi v1 là vận tốc của người so với thuyền thì:  '  ' v1  v1  v2  v1  v1  v2 Ta có: ' l s v  ; v2  1 t t l là chiều dài thuyền, s là đoạn đường thuyền đi được trong thời gian t.
Do đó: ' ls v1  v  v2  1 t ls s Mà: mv1  Mv2  m M t t ml s  1m mM
II. Khối tâm 1.Định nghĩa: Khối tâm G của hệ chất điểm là vị trí thỏa mãn hệ thức: m M G  0 i i i Mi là vị trí chất điểm i 2. Vị trí khối tâm : đối với điểm O trong HQC nào đó được xác định bởi vectơ vị trí rG  OG
Ta có: OG  OM i  M i G   mi OG   mi OM i   mi M i G i i i  mi OM i  OG  i  mi i m r i i   với ri  OM i ; M   mi rG  i M
Tọa độ khối tâm trong hệ tọa độ Descartes: m x i i i m y i i i m z i i i xG  ; yG  ; zG  M M M Khối tâm của vật rắn: chia VR ra làm các phần tử khối lượng dm VCB coi như chất điểm:  dm.x  dm. y  dm.z xG  ;y G  ;z G  M M M x, y, z là tọa độ của phần tử khối lượng dm
Lưu ý: * Với các vật đồng chất mà dạng hình học có yếu tố đối xứng thì khối tâm nằm trên các yếu tố đó. * Trong trọng trường khối tâm trùng với trọng tâm, tuy nhiên khái niêm khối tâm có ý nghĩa cơ bản hơn trọng tâm bởi vì trong tình trạng không trọng lực trọng tâm không còn nhưng khối tâm vẫn có. * Trong trọng trường đồng nhất có gia tốc g thế năng của VR bằng thế năng của khối tâm mang tổng khối lượng.
Nếu hệ S gồm hai hệ S1 và S2 thì: m1 OG1  m2 OG2 OG  m1  m2 • G, G1, G2 là khối tâm của S, S1, S2 • m1, m2 là khối lượng của S1, S2
3) Vận tốc khối tâm d ri d rG  mi dt vG   i dt M  mi vi  pi P  i  i  M M M 4) Gia tốc khối tâm: d vG 1 dP F aG    dt M dt M
5) Phương trình chuyển động của khối tâm F  MaG Vậy khối tâm của hệ chuyển động như một chất điểm có khối lượng bằng tổng khối lượng của hệ và chịu tác dụng của một lực bằng tổng các ngoại lực tác dụng lên hệ đặt tại khối tâm. 6) Nếu F  0 thì : aG  0  vG  const Khối tâm của hệ hoặc đứng yên hoặc chuyển động thẳng đều
Ví dụ 1: Tại ba đỉnh của một tam giác đều cạnh a có đặt ba chất điểm, khối lượng lần lượt bằng m1, m2, m3. Xác định khối tâm của hệ ba chất điểm đó.
Chọn hệ trục tọa độ Oxy như hình vẽ, ta có: m1 x1  m2 x2  m3 x3 xG  m1  m2  m3 a y 0  m2  m3a m2 ●  2 m1  m2  m3 O● ● x m1 m3 m1 y1  m2 y2  m3 y3 yG  m1  m2  m3 a 3 0  m2 0  2 m1  m2  m3
Ví dụ 2: Xác định vị trí khối tâm của một sợi dây đồng chất, khối lượng m được uốn thành một cung tròn AB tâm O bán kính R với góc mở AÔB = 2αo
Vì sợi dây đối xứng qua đường phân giác của góc AÔB nên khối tâm của nó nằm trên đường phân giác này. Chọn trục Ox trùng với đường phân giác. Tọa độ khối tâm: 1 xG   dm.x A m R m m dα dm  dl  .R.d O α x l R.2o x  R cos B o R R  xG  2o  cosd  o sino o