BÀI GI NG V T LÝ ĐI C NG 2Ả Ậ Ạ ƯƠ
Chuyên đ:ề
DÒNG ĐI N KHÔNG ĐIỆ Ổ
(Đ ểdownload tài li u này, hãy đăng nh p ệ ậ
vào di n đànễ c a trang web ủchamphay.com)
Th.S Đ Qu c Huyỗ ố
MỤC TIÊU
Sau khi h c xong ch ng nàyọ ươ , SV phải :
– Nêu đc khái ni m c ng đ, m t đ ượ ệ ườ ộ ậ ộ
dòng đi n.ệ
–V n d ng đc các đnh lu t Ohm, ậ ụ ượ ị ậ
Kirchhoff đ gi i m ch đi n.ể ả ạ ệ
–Tính đc công su t c a dòng đi n, ượ ấ ủ ệ
ngu n đi n.ồ ệ
NỘI DUNG
I – Các khái ni m c b n v dòng đi nệ ơ ả ề ệ
II – Đnh lu t Ohmị ậ
III – Đnh lu t Kirchhoffị ậ
IV – Công, công su t c a dòng đi nấ ủ ệ
V – Công su t, hi u su t c a ngu n đi nấ ệ ấ ủ ồ ệ
VI – Ghép các ngu n đi n gi ng nhauồ ệ ố
I – CÁC K/N CƠ BẢN VỀ DÒNG ĐIỆN:
1 – Dòng đi n, chi u c a dòng đi n:ệ ề ủ ệ
Dòng đi n: ệlà dòng chuy n d i có h ng c a các đi n ể ờ ướ ủ ệ
tích
Chi u c a dòng đi n:ề ủ ệ đc qui cượ ướ là chi u chuy n ề ể
đng c a các đi n tích d ng.ộ ủ ệ ươ
2 – C ng đ dòng ườ ộ
đi n:ệ
dq
Idt
=
q
It
=
DĐKĐ
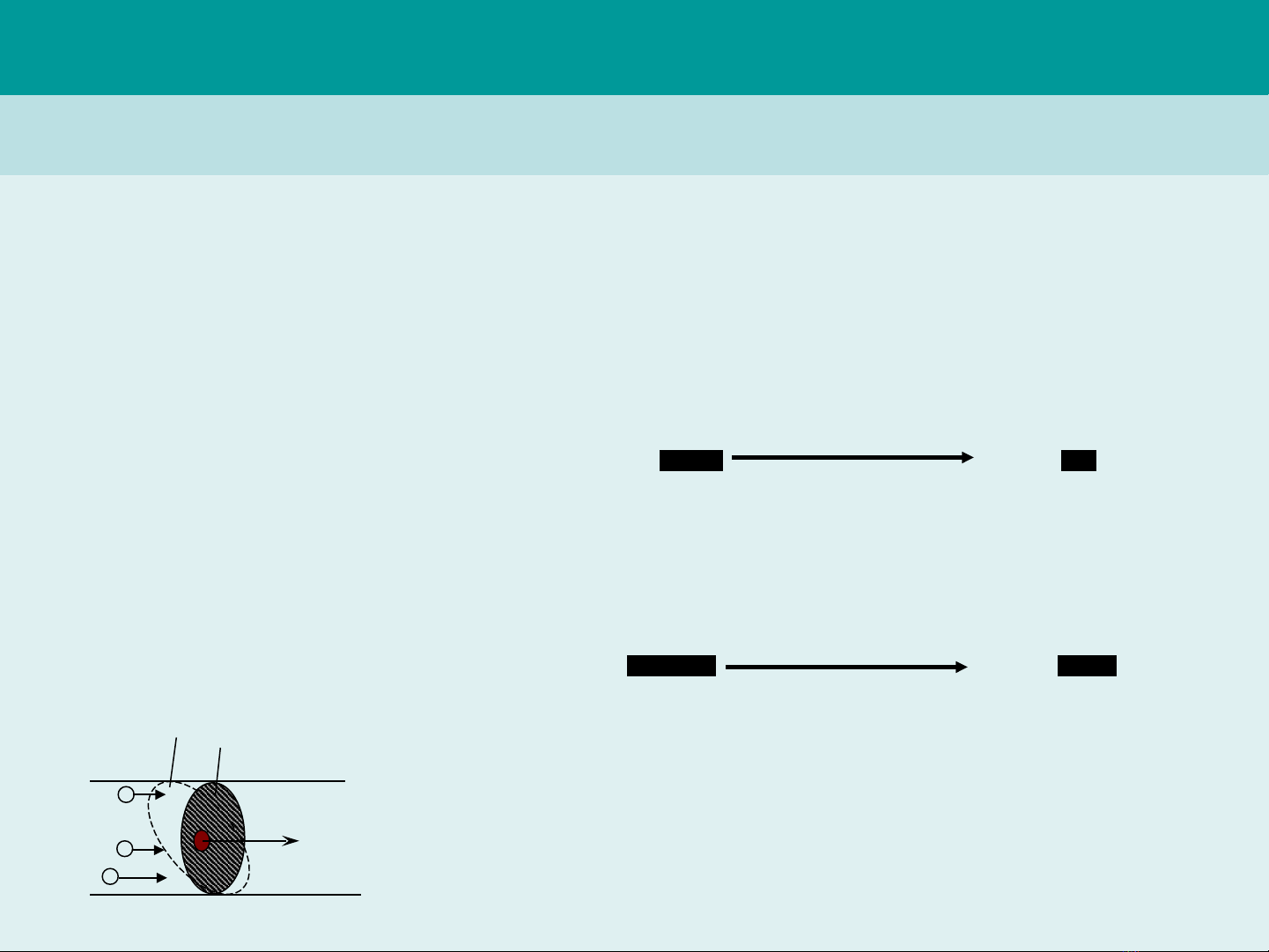
3 – M t đ dòng đi n:ậ ộ ệ
n
dI
jdS
=
n
I
jS
=
p/b đều
+
+
+dSn
SSn
o
j n q v
=
I – CÁC K/N CƠ BẢN VỀ DÒNG ĐIỆN:
Ví d 1:ụ
Mỗi giây có 2.1018 ion dương hóa trị 2 và 4.1018 electron
chạy qua đèn ống có đường kính tiết diện d = 2,0cm.
Tính cường độ dòng điện và trị số trung bình của mật
độ dòng điện j qua đèn.
q q q
It t
+ −
+
= =
Gi iả
2 2 2
n
I I 4I 4.1, 28
jS d / 4 d 3,14.(0,02)
= = = = =
π π
18 19 18 19
2.10 .2.1,6.10 4.10 .1,6.10
1
− −
+
= =
1, 28A
3 2
4,08.10 A / m