Chương 6:
LẤY MẪU & KHÔI PHỤC TÍN HiỆU
Giảng viên: Ths. Đào ThịThu Thủy
CNDT_DTTT 2
Chương 6:
LẤY MẪU & KHÔI PHỤC TÍN HiỆU
6.1 Lấy mẫu và định lý lấy mẫu
6.2 Sự chồng phổ
6.3 Tiền lọc chống biệt danh
6.4 Lấy mẫu quá mức và tiêu hủy
6.5 Mạch khôi phục tương tự
CNDT_DTTT 3
6.1 LẤY MẪU & KHÔI PHỤC TÍN HiỆU
THỜI GIAN LIÊN TỤC
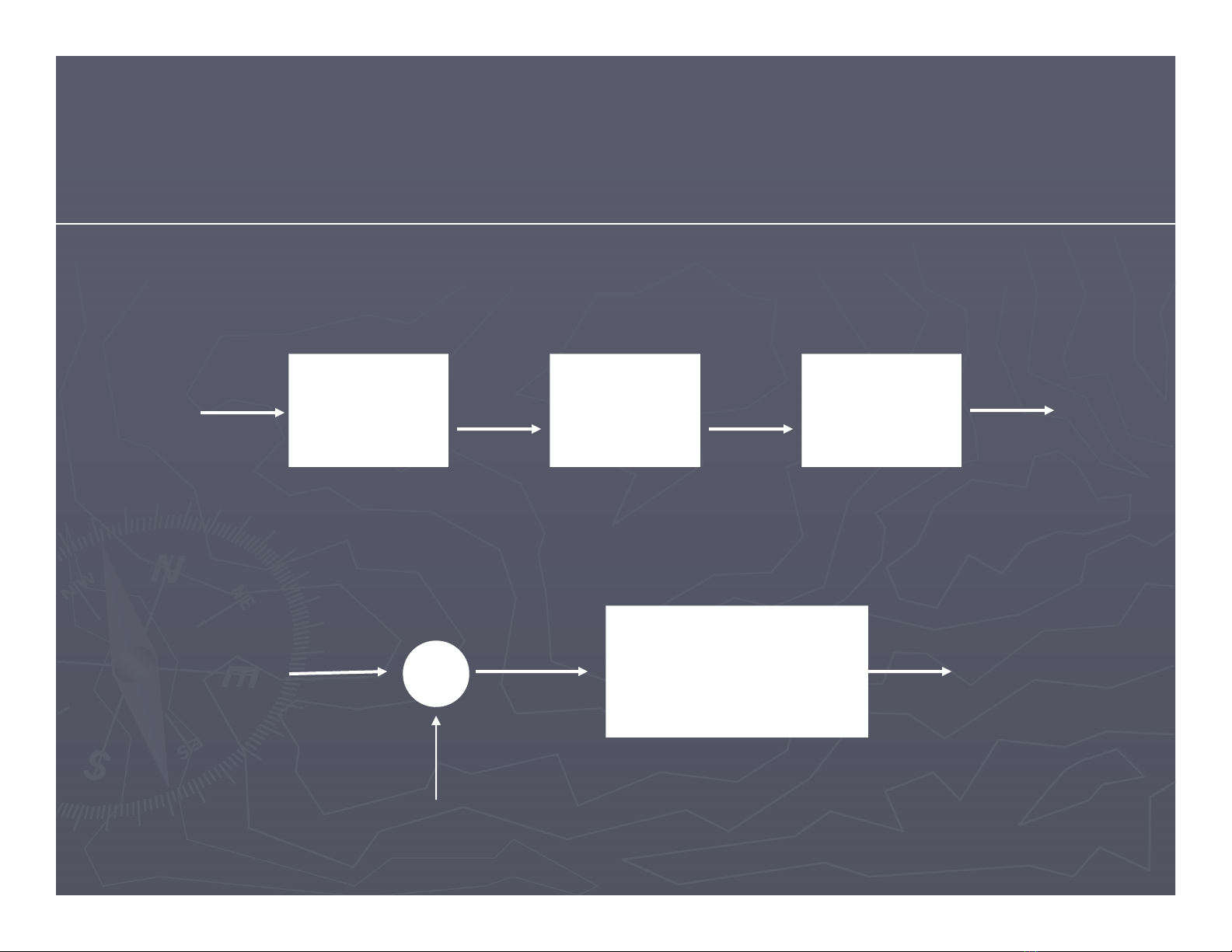
6.1.1 Khái niệmlấymẫutínhiệu
Mã hóa xd(n)
Rời rạc
hóa
xa(t) x(n) Lượng
tử hóa
xq(n)
Chuyển xung
→
mẫu
xa(nTs)
= x(n)
xa(t) X
sa(t)
xs(t)
Quá trình lấy mẫu tín hiệu
CNDT_DTTT 4
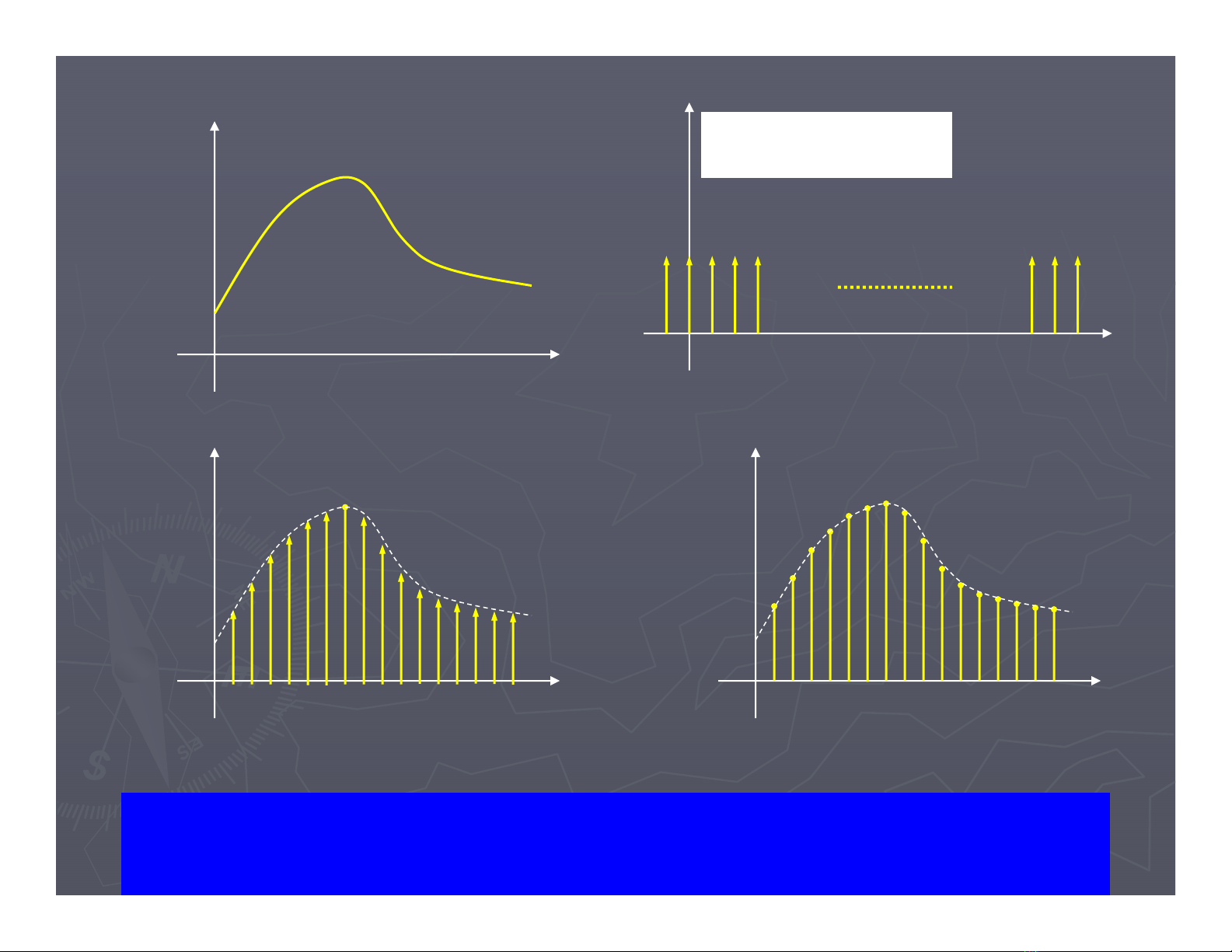
Tín hiệu tương tự
xa(t)
t
0
xa(nTs)
n
0T
s2Ts…
Tín hiệu rời rạcTín hiệu được lấy mẫu
xs(t)
n
0T
s2Ts…
t0
Chuỗi xung lấy mẫu
Ts2Ts…
∑
∞
−∞=
−=
n
sa nTtts )()(
δ
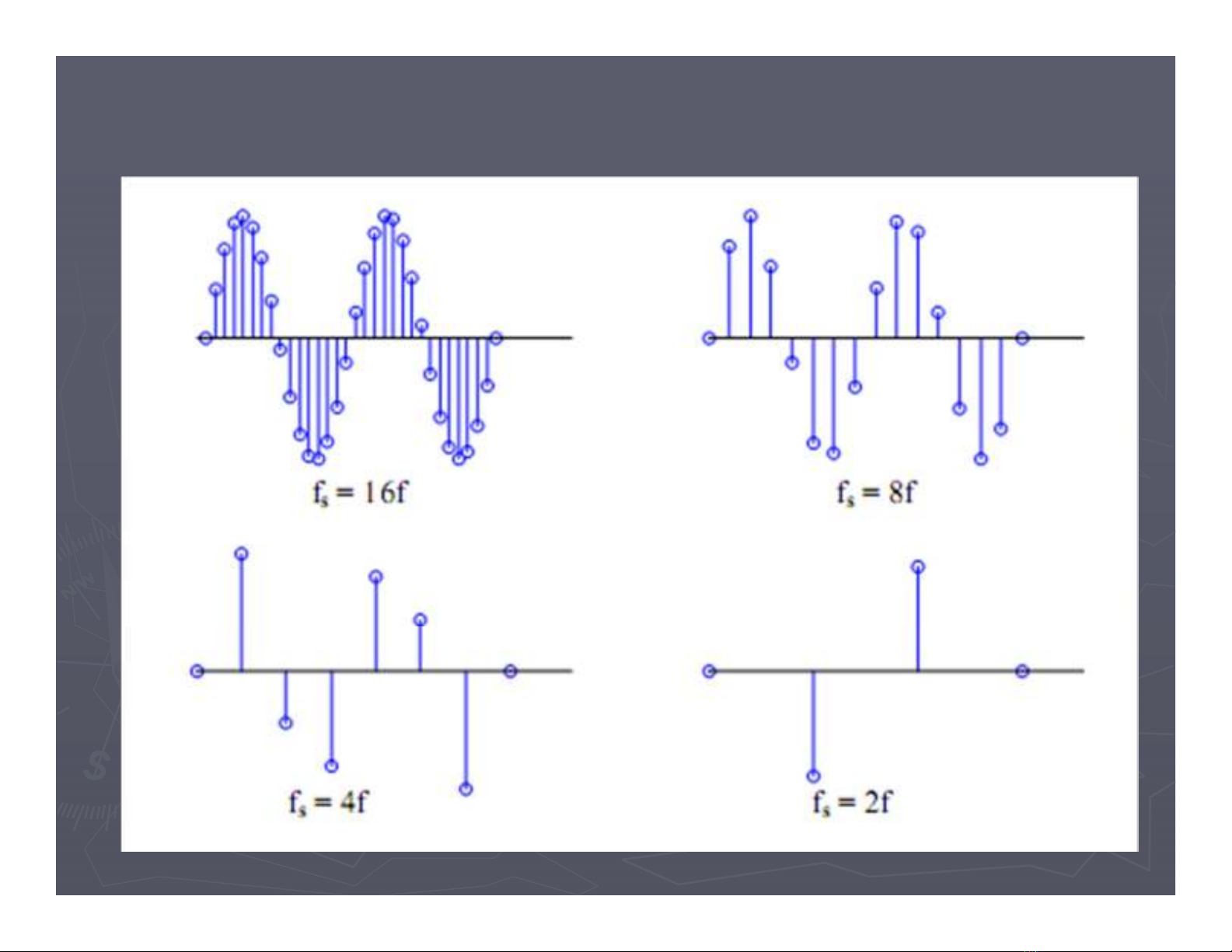
Tốc độ lấy mẫu càng lớn -> khôi phục tín hiệu càng chính xác
CNDT_DTTT 5
Ví dụ lấy mẫu tín hiệu sin