1
Trường đại học Xây Dựng
BÀI TẬP LỚN
CƠ HỌC KẾT CẤU 2
Sinh viên thực hiện : Nguyễn Đức Phúc
Lớp: 53CD4
Khoa: Xây Dựng Cầu Đường
Hà nội, ngày 20 tháng 9 năm 2010
Bài 1: TÍNH HỆ SIÊU TĨNH THEO PHƯƠNG PHÁP LỰC

2
1. Xác định số ẩn số, lập hệ cơ bản
2. thiết lập hệ phương trình chính tắc, xác định các hệ số và các số hạng tự do bằng cách
“nhân” biểu đồ.
3. vẽ các biểu đồ mômen uốn lực cắt và lực dọc.
4. kiểm tra biểu đồ mômen uốn (Mp) bằng cách nhân biểu đồ.
0
k p
M M
và
0
s p
M M
5. xác định chuyển vị đứng tại tiêt diện A.
Bài làm:
1. Xác định số ẩn số, chọn hệ cơ bản.
ta có: 3V – K =3.2 – 4 = 2
hệ có 2 bậc siêu tĩnh.
Chọn hệ cơ bản như hinh 1.1
2. Thiết lập phương trình chính tắc, xác định các hệ số và số hạng tự do bằng cách nhân
biểu đồ. Giải hệ phương trình chính tắc.
5m
6m 4m 5m
3m
EA=82EI 2EI
4EI
4EI
4EI
30KN/m²
30KN/m²
180KN 200KNm
5m
6m 4m 5m
3m
EA=82EI 2EI
4EI
4EI
30KN/m²
30KN/m²
180KN 200KNm
X1
X1X2
X2

3
5m
6m 4m 5m
3m
EA=82EI 2EI
X1
X1
=1
=1
=1
X2
X2
=1
=1
5m
6m 4m 5m
3m
EA=82EI
5m
6m 4m 5m
3m
EA=8
2.1. thiết lập phương trình chính tắc
phương trình chính tắc dạng chữ:
11 1 12 2 1
21 1 22 2 2
0
0
P
P
X X
X X
vẽ biểu đồ mômen
0
1 2
; ;
P
M M M
2
M
(M0P)
(M0P)
Xác định các hệ số trong phương trình chính tắc:
11 1 1
1 1 2 1 1 2 1 1 2 1 1 2 1703
. 8.6 . .8 5.5 .5 3.5 . .3 8.8 .8
4 2 3 2 2 3 4 2 3 2 2 3 12
M M
EI EI EI EI EI
22 2 2
1 1 2 1 1 2 1 1 2 1 1501
4.6 3 4.5 4 5.5 5 5.8 .5
4 2 3 4 2 3 4 2 3 2 12
M M
EI EI EI EI EI

4
12 21 1 2
1 1 2 1 1 2 1 1 59
5.8 4 3.5 4 8.8 5
4 2 3 4 2 3 2 2
M M
EI EI EI EI
1 1
1 1 2 1 1 2 1 1 2
5.8 1400 5.5 900 300.5 3
4 2 3 2 2 3 4 2 3
1 2 1 1 1 2 2 7805
5.75 3 960.8 8 240.8 4
4 3 2 2 2 3 3 4
P P
M M EI EI EI
EI EI EI
0
2 2
1 1 2 1 1 2 2
4.6 1400 300.5 4 75.5 2
4 2 3 4 2 4 3
1 9575
+ 5.8 240
2
P P
M M EI EI
EI EI
Phương trình chính tắc:
1 2
1 2
1703 185 7805
= 0
12 3 4
185 1501
7975 =0
3 12
X X
EI
X X
1
2
52.755
89.766
X
X
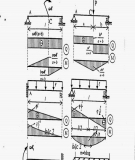
Biểu đồ (Mp), (Qp), (Np):
( Mp)
5m
6m 4m 5m
3m
EA=8
533,324
616,55
516,445
897,075
283,226

5
( Qp)
( Np)
Biểu đồ
1 2
S
M M M
có dạng như hình vẽ:
5m
6m 4m 5m
3m
EA=8
88,887
123,31
3,3548
116,645
103,29 56,69
296,69
5m
6m 4m 5m
3m
EA=8
180
135,59
103,289
56,690
13,378
16,621