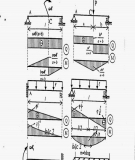
Chương 2: THANH CH U KÉOỊ (NÉN) ĐÚNG TÂM
2.1. Tóm tắt lý thuy tế
2.1.1. Đ nịh nghĩa
Thanh đ cượ gọi là chịu kéo ho cặ n nế đúng tâm n uế trên mặt c tắ ngang
của nó chỉ tồn t iạ một thành ph nầ ứng l cự là Nz
Qui ước d uấ của Nz: chi uề dưnơg khi đi ra khỏi m tặ c tắ (chịu kéo), và
chi u âmề khi hưngớ vào trong m tặ c tắ ngang đang xét (chịu nén).
2.1.2. nỨg suất
Trên m tặ c tắ ngang chỉ tồn t iạ thành ph n ầ ứng su tấ pháp. Tr ngạ thái ứng
su t t iấ ạ một điểm của thanh là tr ngạ thái ứng su tấ đ n.ơ
N
z
σ
z
=
A
(2.1)
Trong đó A - di nệ tích m tặ c tắ ngang, Nz - l cự dọc trên m tặ cắt ngang
2.1.2. Bi nế d ngạ
- Bi nế dạng dài tuy tệ đối dọc trục thanh
l N dz
Δl
=
∫
z(2.2a)
0 EA
Trong đó l - chi uề dài thanh, EA - độ c ngứ khi kéo (nén) của thanh
n uế trên đo nạ chi uề dài l
mà
Δl
=
N
z
l
EA
N z
=
const
EA thì
(2.2b)
N uế thanh gồm n đo n,ạ chi uề dài và độ c ngứ khi kéo (nén) trên mỗi đoạn là
li
và (EA)i , l cự dọc trên mỗi đoạn là Nzi
và
N
z
=
const
EA trên mỗi đo nạ thì:
n n
⎛
N l
⎞
∑i
∑
⎜⎟
Δl
=
Δl
i
=
1

=
zi i
i
=
1
⎝
(EA)i
⎠
(2.3)
- Bi nế d ngạ ngang tuy tệ đối theo phương x, y vuông góc trục thanh

N
∫ ∫
0
2
Δl
=
bε
= −
με
=
−
μ
b
σ
z
=
−
μ
b N z ; Δl
= −
μ
h N z(2.4)
xx
z
b
EEA yEA
v iớ b, h lần l t làượ kích th cướ theo phương x, y của m tặ c tắ ngang có l cự
dọc là Nz, di nệ tích m tặ c tắ ngang là A, μ là hệ số Poisson.
2.1.3. Chuy nể vị
Khi thanh th ngẳ chịu kéo (nén) đúng tâm trục thanh v nẫ th ng, cácẳ m tặ cắt
ngang không có chuy nể vị xoay mà chỉ có chuy nể vị t nịh ti n theoế phương dọc
trục. T iạ toạ độ z của m tặ c tắ ngang, chuy nể vị theo phương dọc trục là w:
z N dz
w
=
∫
z
+
w(2.5)
0 EA
Trong đó w0 là chuy nể vị của m tặ c tắ ngang t iạ z=0
Khi tính chuy n ểvị của các điểm thuộc hệ thanh liên k tế kh p,ớ tr cướ tiên
xác đ nịh l cự dọc trong các thanh, từ đó tính đ cượ bi nế dạng của t ngừ thanh riêng
biệt. Từ sơ đ ồbi nế dạng của hệ tìm mối liên hệ hình học của chuyển vị đi mể
c nầ tìm với bi nế dạng của t ngừ thanh riêng bi t.ệ
2.1.4. Thế năng bi nế d nạg đàn hồi
Th ếnăng bi nế dạng đàn hồi riêng (là thế năng biến dạng đàn hồi tích lũy
trong 1 đ nơ vị thể tích thanh)
u
=
1 σ
ε
=
1
σ
2
=
1z(2.6)
2z
z
2Ez2E A2
Thế năng bi nế dạng đàn hồi tích luỹ trong cả đo nạ thanh có chi uề dài l là:
N 2
U
=
udV
=
z
dz
l 2EA
2.1.5. Tính toán đi uề ki nệ b nề và đi uề kiện cứng
Trình tự tính toán đi uề ki nệ b nề của thanh theo ứng su tấ cho
phép:
•Vẽ bi uể đồ l cự dọc Nz của thanh
(2.7)

•Căn cứ vào bi uể đồ l cự dọc và di nệ tích m tặ c tắ ngang trên t nừg đoạn,
tìm
m tặ c tắ ngang nguy hiểm là m tặ c tắ ngang có ứng su tấ pháp c cự trị.
•Xem v tậ li uệ thanh là d oẻ hay dòn để vi tế đi uề ki nệ b nề cho đúng

σ
b b
k n
⇒ V tậ li uệ d o:ẻ
max
{
σ
, σ
}
=
max
⎧
Nz
⎫
≤
[
σ
]
=
ch (2.8a)
zmax z min
⎨
A
⎬
n
⎩ ⎭
Trong đó
[
σ
]
- ứng su tấ cho phép của v tậ li uệ d o,ẻ
σ
ch
của v tậ liệu, n là hệ số an toàn
⇒ V tậ li uệ dòn:
là gi iớ h nạ chảy
σ
≤
[
σ
]
=
σ
b; σ
≤
[
σ
]
=
σ
b(2.8b)
zmax knz min nn
Trong đó
[
σ
]
,
[
σ
]
- ứng su tấ cho phép khi kéo và nén của vật li uệ
dòn,
σ
k
,
σ
n
k n
là gi iớ hạn b nề kéo và nén của v tậ li u,ệ n là hệ số an toàn
Từ đi uề ki nệ b nề ta có ba d ngạ bài toán cơ
b n a.ả Bài toán ki ể m t r a đ i uề k i nệ b nề
Cho: sơ đồ k tế c u,ấ kích th cướ hình học, v tậ li u,ệ tải
trọng. Yêu cầu: kiểm tra điều ki nệ b nề (2.8a) ho cặ (2.8b)
của thanh b. Bài toán c họ n kích t h cướ m tặ c tắ ngan g thanh
Cho: sơ đồ k tế cấu, chi uề dài thanh, hình d ngạ thanh, v tậ li u,ệ t iả tr ngọ
Yêu c u:ầ Chọn kích th cướ c nầ thi tế của m tặ c tắ ngang theo đi uề ki nệ b n.ề
A
≥
N
z
[
σ
]
(2.9)
c. Bài toán tìm giá t r ị cho phép c ủ a t iả t r ngọ
Cho: sơ đồ k tế c u,ấ kích th cướ hình học, v tậ li u,ệ vị trí và ph ngươ chi uề
của t iả trọng.